AVL树的实现
文章目录
- 介绍
- 原理
- 1、失去平衡的四种情况即相应的旋转操作
- 2、增添
- 3、删除
- 代码实现(C++)
介绍
AVL树是最先被发明的自平衡二叉查找树,也被称为高度平衡树。相比二叉查找树,它的特点是AVL树中任何结点的两个子树的高度差别最大为1。AVL树的查找、插入和删除在平均和最坏情况下都是O(logn)
原理
1、失去平衡的四种情况即相应的旋转操作
LL
根的左子树的左子树还有非空子结点,导致根的左子树的高度比根的右子树的高度大2

RR
根的右子树的右子树还有非空子结点,导致根的右子树的高度比根的左子树的高度大2
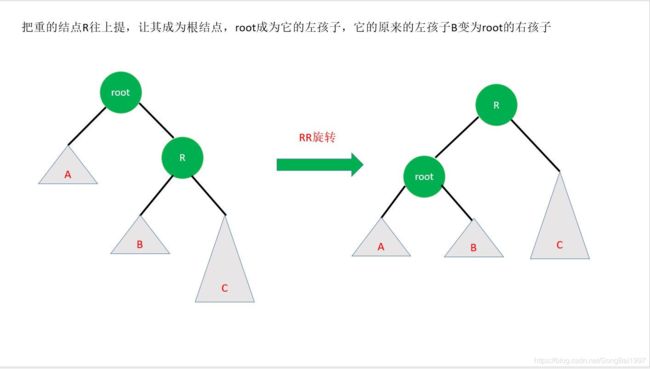
LR
根的左子树的右子树还有非空子结点,导致根的左子树的高度比根的右子树的高度大2
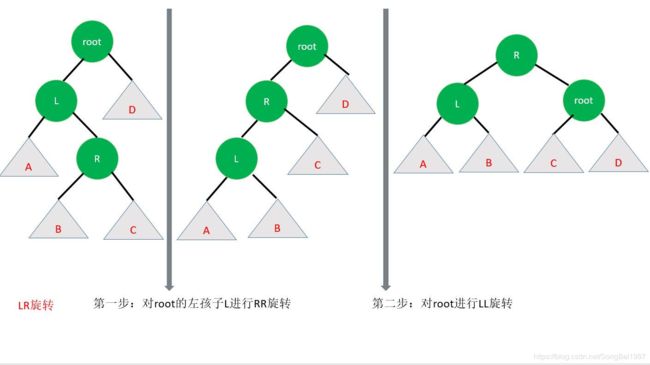
RL
根的右子树的左子树还有非空子结点,导致根的右子树的高度比根的左子树的高度大2
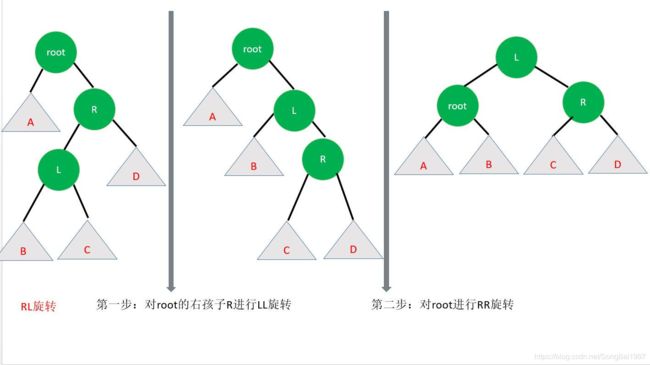
2、增添
//将键值为key结点插入AVL树中
template<class T>
Node<T>* AVLTree<T>::insert(Node<T>* &tree,T key)
{
if(!tree)
{
tree=new Node<T>(key,NULL,NULL);
if(!tree)
{
cout<<"创建结点失败!"<<endl;
return NULL;
}
}
else if(key<tree->key)//key应该插入tree的左子树
{
tree->l=insert(tree->l,key);
//插入结点后,若AVL树失去平衡,则进行相应的调整
if(height(tree->l)-height(tree->r)==2)
{
if(key<tree->l->key)
tree=LL(tree);
else
tree=LR(tree);
}
}
else if(key>tree->key)//key应该插入tree的右子树
{
tree->r=insert(tree->r,key);
//插入结点后,若AVL树失去平衡,则进行相应的调整
if(height(tree->r)-height(tree->l)==2)
{
if(key<tree->r->key)
tree=RL(tree);
else
tree=RR(tree);
}
}
else
{
cout<<"不允添加相同的结点!"<<endl;
}
tree->h=max(height(tree->l),height(tree->r))+1;
return tree;//返回根结点
}
template<class T>
void AVLTree<T>::insert(T key)
{
insert(root,key);
}
3、删除
//删除结点z
template<class T>
Node<T>* AVLTree<T>::remove(Node<T>* &tree,Node<T> *z)
{
//根为空或者没有要删除的结点,直接返回NULL
if(!tree||!z) return NULL;
if(z->key<tree->key)//待删除结点在tree的左子树中
{
tree->l=remove(tree->l,z);
//删除结点后,若AVL树失去平衡,则进行相应的调整
if(height(tree->r)-height(tree->l)==2)
{
if(height(tree->r->l)>height(tree->r->r))
tree=RL(tree);
else
tree=RR(tree);
}
}
else if(z->key>tree->key)//待删除结点在tree的右子树中
{
tree->r=remove(tree->r,z);
//删除结点后,若AVL树失去平衡,则进行相应的调整
if(height(tree->l)-height(tree->r)==2)
{
if(height(tree->l->l)>height(tree->l->r))
tree=LL(tree);
else
tree=LR(tree);
}
}
else//tree对应要删除的结点
{
//tree的左右孩子都非空
if(tree->l&&tree->r)
{
//tree的左子树比右子树高
if(height(tree->l)>height(tree->r))
{
//找出tree的左子树中的最大结点,将其键值赋给tree,然后删除它
Node<T>* maxNode=maximum(tree->l);
tree->key=maxNode->key;
tree->l=remove(tree->l,maxNode);
}
//tree的右子树的高度大于或等于左子树高度
else
{
//找出tree的右子树中的最小结点,将其键值赋给tree,然后删除它
Node<T>* minNode=minimum(tree->r);
tree->key=minNode->key;
tree->r=remove(tree->r,minNode);
}
}
//tree的左右孩子只要有一个为空
else
{
Node<T>* tmp=tree;
tree=(tree->l)?tree->l:tree->r;
delete tmp;
}
}
return tree; //返回根结点
}
template<class T>
void AVLTree<T>::remove(T key)
{
Node<T> *z=search(root,key);
if(z) root=remove(root,z);
}
代码实现(C++)
#include