数据预处理--数据检查、变量标准化、分布变换、构造特征、特征筛选

一、数据检查

1）缺失值

有时候是null,有时候全是0，这个需要比想象中更仔细，因为取数的同学们有时候会默认填充0，有时候是因为数据库迁移，产品刚刚发布所以太远的数据没有等原因造成的，这些需要及时确认

对于有些变量仅对特定的人有值，（比如说理财的产品偏好，当然只有买了理财的人才会有偏好数据可以分析），可以给没有这个值的人填充一个数值，可以是999这样这个字段不会取到的大值（但是要注意在模型中把该字段当成是定序或者分类变量处理，不然在线性模型中会因为是极值而带坏模型），也可以根据意义考虑一下没有值是否比有值的人更不活跃等，给-1

2）没有变异性的变量

可以通过计算每列的std，把那些几乎没有variation的变量删掉

3）逻辑检查

不应该有负数的，不应该是0的，但是出现了这样的错误，年龄很大的（115岁），逻辑上异常的数有可能是数据提取时计算出了差错，也有可能就是数据在一开始录入有问题，又或者真有其事（活到115岁也没啥，子女持有账户blablabla），建议检查完后对逻辑上奇怪的记录做删除处理，有可能会误导模型的学习

4）异常值（极值）

1. 3sigma原理，但是均值和标准差可以考虑不用全量数据，例如去掉最大最小的5%，1%数据后，再计算标准差和均值
2. box-plot 小于和超过的数被认为是极值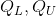，分别是下四分位点和上四分位点, 四分位数鲁棒性比较强，上下25%的数可以任意大任意小而不影响四分位数取值，故而识别异常值比较客观
3. 机器学习模型：聚类（基于距离，基于密度），OneClassSVM 

对异常值的操作可以使删除整条记录，也可以划归到边界值上，或者对超过某个数值的数使用bin等

利用分位数查找极值（extreme_value_ratio正常等于1.5，根据具体情况可大可小）

def is_extreme(QL, QU, value):
    if value <= QL - EXTREME_VALUE_RATIO * (QU - QL) or value >= QU + EXTREME_VALUE_RATIO * (QU - QL):
        return True
    else:
        return False


def get_quartile(value_list):
    def split_half(value_list):
        value_list = sorted(value_list)
        mid_pos, is_odd = divmod(len(value_list), 2)
        if is_odd:
            return value_list[:mid_pos], value_list[mid_pos+1:], value_list[mid_pos]
        else:
            return value_list[:mid_pos], value_list[mid_pos:], sum(value_list[mid_pos-1:mid_pos+1])/2
    part1, part2, q5 = split_half(value_list)
    part11, part12, q25 = split_half(part1)
    part21, part22, q75 = split_half(part2)
    return q25, q5, q75

lower_quartile, _, upper_quartile = get_quartile(value_list)
is_extreme(lower_quartile, upper_quartile, value)

二、标准化

原因：

1）使不同量纲的变量对目标变量的影响具有可比性，涉及到距离的计算，如kmeans，和变量间方差的计算，如PCA，则必须先做标准化，不标准化的话，量级大的变量影响大

2）梯度下降法中加速模型收敛，圆形的梯度方向直指圆心，而椭圆的梯度方向比较迂回，最终可能都找不到最优解

但也不是所有模型都需要标准化，过去的建模经验是像决策树这样的模型不标准化效果反而更好

常见方法：

1）归一化

把变量的取值归到（0,1）之间或（-1,1）之间，常见的有(x-min) / (max-min)

2）标准化

z-score: (x-min) / std

将正态分布的标量规约到服从N（0,1）

3）中心化（去均值）

参考：

https://blog.csdn.net/resourse_sharing/article/details/51979494

https://www.jianshu.com/p/1e63cd2afedc?from=timeline

 

三、分布变换

数据的正态性对于统计量的各种小样本性质，统计量的有限样本分布，极大似然估计都很重要

中心极限定理告诉我们当样本数趋向于无穷大时，样本的分布会接近正态分布，但有些变量本身的分布就不是正态的，那么对于一些有正态假设的检验，估计的模型来说，就需要事先对变量做分布变换

另一方面极大或极小的值经过变换后跟正常值差距缩小，减少了极值对模型的扰动

1）平方根变换

适用poisson等计数变量

2）倒数变换

服从二项分布或是两端波动较大的变量

3）log变换

自然界的大多数分布是指数分布，如果是钱数，人数，大体上log后呈现正态分布

取对数可以消除异方差。

取对数可以使非线性的变量关系转化为线性关系，更方便做参数估计。

y和x本来就不是线性关系，而是log(y)跟x是线性关系，log(y1)-log(y0)约等于增长率r，真实的关系可能是x每增加一单位，增长率不变（log(1+r)~r）

4）box-cox变换

1,2,3是box-cox的在lambda等于0.5,01,0时的特殊情况

box-cox对于正态性，样本间的方差齐性都有很好的修正作用，它的原理是引入lambda对y做变换，通过对变换后的y拟合线性模型，找到最优的lambda，使得变换后的变量基本服从线性模型的假设

 

四、分箱

分箱即是把连续变量离散化，它的好处是

1）突出变量间的关联，对涉及到距离的算法都会比较明显，例如age这个变量，24和26可能没什么区别，但是如果变成是20-25一组，26-30一组，我们就可能看到age和目标变量之间的关联

2）方便构造交叉变量，例如age*gender,可帮助在线性模型中引入非线性

3）提高模型稳定性，分箱使极值划归到某个区间范围内，减小了极值扰动

4）分箱后进行one-hot操作，每个类别具有一个单独的系数，可以增强拟合

方法：

1）等距 

2）等频

3）专家法：根据业务的含义来确定分割点

4）iv最大

5）最小熵法

使变量能最大限度区分因变量的各类别的切分

6）卡方分箱法ChiMerge

相邻区间的类分别如果类似则合并，缺点是需要预排序，如果是U型或非线性则难以合并两端的区间

参考：

https://blog.csdn.net/m0_37235489/article/details/82148749

https://www.jianshu.com/p/b1b1344bd99f

 

五、构造特征

当特征有限，特征数量有限，或者有用的特征有限时，可以尝试构造特征

1. 对有用的字段，可以看这个变量时间维度的滞后项是否也显著，具体方法是用y对x做回归，把x的滞后项陆续加进模型，看是否显著，如果显著，则将该滞后项加入到模型的自变量组中

2.变化率 过去一个月/过去三个月，过去三个月/过去6个月，过去6个月/过去一年等，通常也会先将过去三个月的减去过去一个月的，过去6个月的减去过去三个月的，再构造上述增长特征

3.单次金额 如果有3个月内消费金额，和消费次数，可以构建笔均消费金额

4.最大值最小值变化

 

六、相关性和共线性

 

 

七、特征筛选

1. 岭回归（L1正则），通过让不重要的变量的系数变成0来实现冗余变量的剔除

（Lasso回归（L2正则），主要用来预防过拟合）

2. 前向回归和后向回归forward regression and backward regression

前向选择：根据BIC，AIC等准则，每一次将让模型拟合优度提升最大的变量筛选出来，加入到变量列表里

后向选择：每次把对拟合优度影响最小的变量从变量列表中踢出去

3. 决策树类模型的变量重要性feature importance

变量被使用的次数，次数越多变量越重要

去掉某个变量，看模型的accuracy下降多少，下降越多的变量越重要

https://scikit-learn.org/stable/modules/ensemble.html#random-forest-feature-importance

4.PCA降维

用崖底碎石图scree plot来确定最终选择多少变量

PCA的缺点是改变了原有的变量，需要给出合理解释