数据结构与算法实验报告--哈夫曼编码
| 实验 |
实验三 Huffman编码的实现 |
| 学院 |
|
| 专业(班级) |
|
| 姓名 |
|
| 学号 |
|
| 教师 |
|
实验二 Huffman编码的实现
1实验目的
1. 掌握二叉树的存储结构。
2. 掌握二叉树的遍历操作的实现方法。
3. 掌握建立Huffman树及求Huffman编码的操作,加深对二叉树应用的理解。
2实验要求
1. 二叉树采用二叉链表存储结构
2. 二叉树的遍历操作可以用递归算法实现
3实验环境
硬件平台:计算机CPU 主频2.0G以上;内存128兆以上;
软件平台:Windows2003或以上版本,Visual C++6.0。
4实验内容
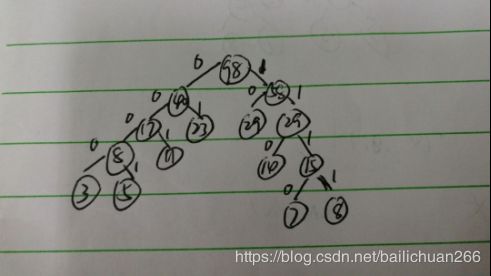
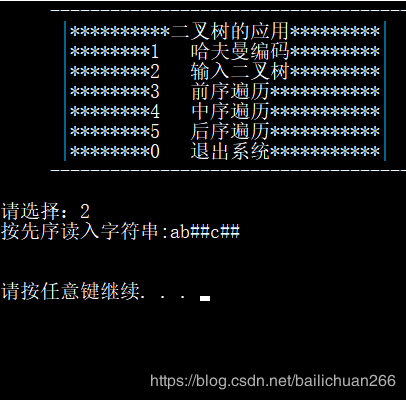
1. 设计一棵二叉树,输入完全二叉树的先序序列,用#代表虚结点(空指针),如ABD###CE##F##,建立二叉树。
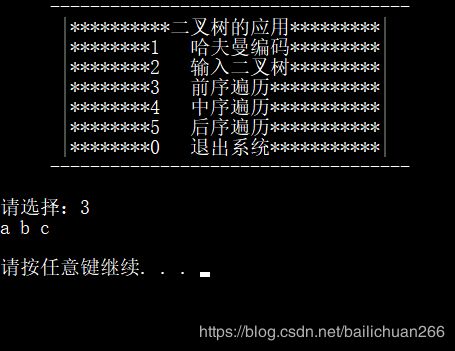
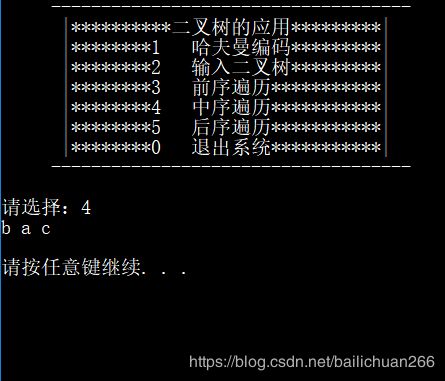
2. 实现二叉树的前序、中序和后序遍历。
3. 设计一个哈夫曼编码系统, 根据字符频率构造哈夫曼树,并给出每个字符的哈夫曼编码。
5实验步骤
- 问题分析:利用哈夫曼编码进行通信可以大大提高信道利用率,缩短信息传输时间,降低传输成本。但是这要求在发送端通过一个编码系统对待传数据预先编码,在接收端将传来的数据进行译码。对于双工信道,每端都需要一个完整的编码/译码体系。本次实验通过学习课上学习的知识,实现哈夫曼编码。通过输入的字符建立二叉树,先序,中序,后序输出相应的字符串。
2.需求分析:
(1)初始化:从键盘输入n个字符的权值,建立哈夫曼树。
(2)建立哈夫曼树。
(3)编码:利用建好的哈夫曼树对各权值进行编码,输出各权值的哈夫曼编码。
(4)初始化二叉树:输入完全二叉树的先序序列,用#代表虚结点(空指针),如ABD###CE##F##,建立二叉树。
(5)先序,中序,后序遍历二叉树。
(6)输出遍历字符串。
3.概要设计:
//---------赫夫曼树的存储结构----------
typedef struct{
unsigned int weight;
unsigned int parent,lchild,rchild;
}HTNode,*HuffmanTree;
typedef char **HuffmanCode;
Void HuffmanCoding(HuffmanTree &HT,HuffmanCode &HC,int *w,int n)
//求赫夫曼编码
//-------------二叉树存储结构
typedef struct BiTNode{
TElemType data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
Status CreateBiTree(BiTree &T)
//建立二叉树
void PreOrderTraverse(BiTree T)
//先序遍历二叉树
void InOrderTraverse(BiTree T)
//中序遍历二叉树
void PostOrderTraverse(BiTree T)
//后序遍历二叉树
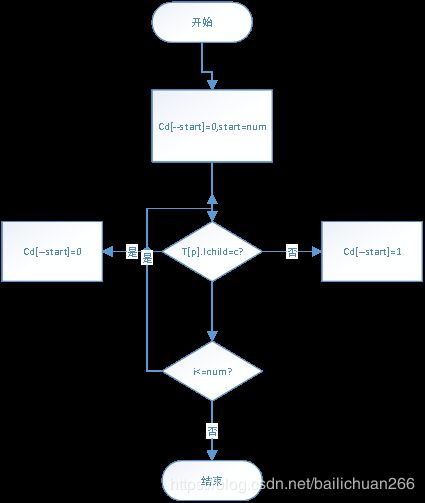
void Select(HuffmanTree &HT, int n, int &s1, int &s2)
//选出权值最小的两个权值
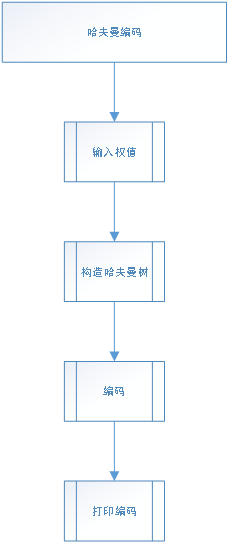
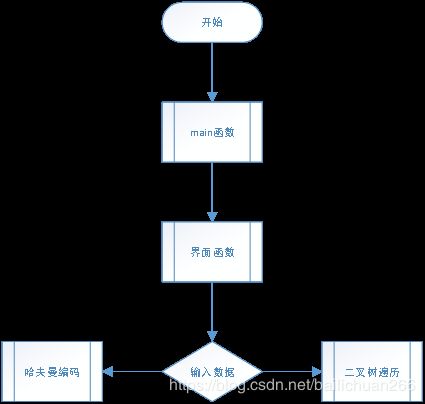
4.功能结构图
构造哈夫曼树
哈夫曼编码
系统流程
5.运行结果
哈夫曼编码
构建二叉树
先序遍历
中序遍历
后序遍历
6.程序源码:
//哈夫曼树构造原则: 权值小的在前,相等的单节点在前;
#include
#include
#include
#include
#include
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
#define LIST_INIT_SIZE 100
#define LISTINCREMENT 10
using namespace std;
typedef char TElemType ;
typedef int Status ;
typedef struct{
unsigned int weight;
unsigned int parent,lchild,rchild;
}HTNode,*HuffmanTree;
typedef char **HuffmanCode;
typedef struct BiTNode{
TElemType data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
Status CreateBiTree(BiTree &T){
char ch;
scanf("%c",&ch);
if('#'==ch)
T=NULL;
else{
T=new BiTNode;
T->data=ch;
CreateBiTree(T->lchild);
CreateBiTree(T->rchild);
}
}
Status Visit(TElemType e){
printf("%c ",e);
return OK;
}
void PreOrderTraverse(BiTree T){
if(T)
{
printf("%c ",T->data);
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
}
void InOrderTraverse(BiTree T){
if(T)
{
InOrderTraverse(T->lchild);
printf("%c ",T->data);
InOrderTraverse(T->rchild);
}
}
void PostOrderTraverse(BiTree T){
if(T)
{
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
printf("%c ",T->data);
}
}
void Select(HuffmanTree &HT, int n, int &s1, int &s2)
{
//在HT[1..n]中选择parent为0且weight最小的两个结点,
// 其序号分别为s1和s2。
int i;
s1=-1;s2=-1;
for(i=1; i<=n; i++)
if(HT[i].parent == 0)
{
if(s1 == -1)
s1 = i;
else if(HT[i].weight < HT[s1].weight)
{
s2 = s1;
s1 = i;
}
else if(s2 == -1 || HT[i].weight < HT[s2].weight)
s2 = i;
}
}
void HuffmanCoding(HuffmanTree &HT,HuffmanCode &HC,int *w,int n)
{
// 并求出n个字符的哈夫曼编码HC
int i, m, s1, s2, start;
char *cd;
unsigned int c, f;
if (n<=1) return;
m = 2 * n - 1;
HT = (HuffmanTree)malloc((m+1) * sizeof(HTNode)); // 0号单元未用
for (i=1; i<=n; i++) { //初始化
HT[i].weight=w[i-1];
HT[i].parent=0;
HT[i].lchild=0;
HT[i].rchild=0;
}
for (i=n+1; i<=m; i++) { //初始化
HT[i].weight=0;
HT[i].parent=0;
HT[i].lchild=0;
HT[i].rchild=0;
}
for (i=n+1; i<=m; i++) { // 建哈夫曼树
// 在HT[1..i-1]中选择parent为0且weight最小的两个结点,
// 其序号分别为s1和s2。
Select(HT, i-1, s1, s2);
HT[s1].parent = i; HT[s2].parent = i;
HT[i].lchild = s1; HT[i].rchild = s2;
HT[i].weight = HT[s1].weight + HT[s2].weight;
}
//--- 从叶子到根逆向求每个字符的哈夫曼编码 ---
cd = (char *)malloc(n*sizeof(char)); // 分配求编码的工作空间
cd[n-1] = '\0'; // 编码结束符。
for (i=1; i<=n; ++i) { // 逐个字符求哈夫曼编码
start = n-1; // 编码结束符位置
for (c=i, f=HT[i].parent; f!=0; c=f, f=HT[f].parent)
// 从叶子到根逆向求编码
if (HT[f].lchild==c) cd[--start] = '0';
else cd[--start] = '1';
HC[i] = (char *)malloc((n-start)*sizeof(char));
// 为第i个字符编码分配空间
strcpy(HC[i], &cd[start]); // 从cd复制编码(串)到HC
}
free(cd); //释放工作空间
} //HuffmanCoding
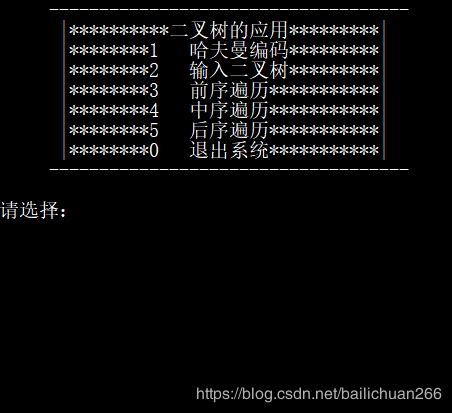
void mainview_user( ) //界面函数
{
BiTree T;
int c;
while(1)
{
system("CLS"); //清除屏幕函数
printf(" ------------------------------------\n");
printf(" |**********二叉树的应用*********|\n");
printf(" |********1 哈夫曼编码*********|\n");
printf(" |********2 输入二叉树*********|\n");
printf(" |********3 前序遍历***********|\n");
printf(" |********4 中序遍历***********|\n");
printf(" |********5 后序遍历***********|\n");
printf(" |********0 退出系统***********|\n");
printf(" ------------------------------------\n");
printf("\n");
printf("请选择:");
scanf("%d",&c);
switch(c)
{
case 1: {
int i,n;
int *w;
HuffmanTree HT;
HuffmanCode HC;
printf("请输入要输入权值的数量:");
scanf("%d",&n); //权值个数
w=(int *)malloc(n*sizeof(int));
printf("Input weights:");
for ( i=0;i