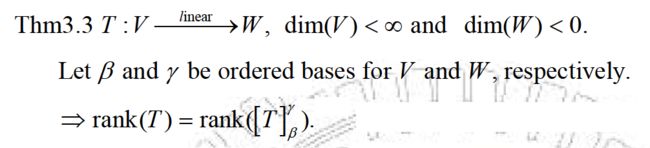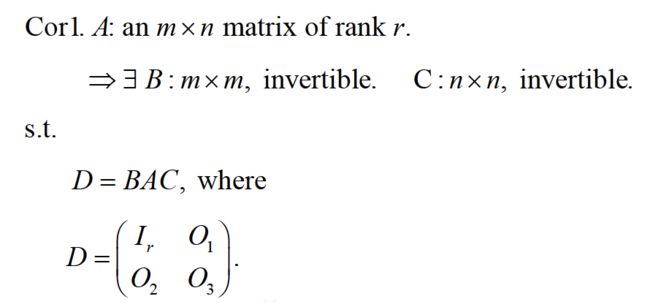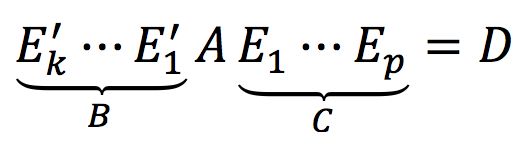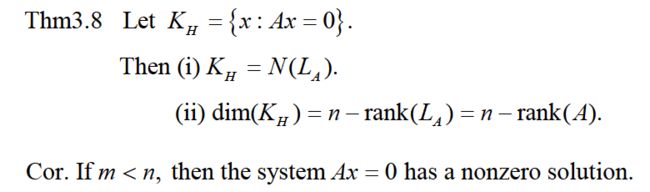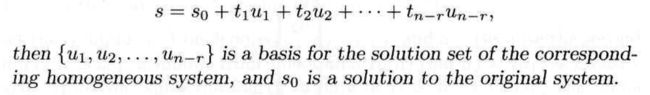线性代数笔记(3):基本矩阵操作与线性方程组的解
一、Elementary Matrix Operations and Elementary Matrix
二、矩阵B由矩阵A经过基本矩阵操作而得到,则必有B=AE(或B=EA)
Here E1 and E2 are elementary matrices obtained from Im and In, respectively, by performing the same elementary row and column operations as those which were performed on A to obtain B.
Theorem 3.2. Elementary matrices are invertible, and the inverse of an elementary matrix is an elementary matrix of the same type.
三、矩阵的秩
我们之前已经定义过线性变换T的rank,可以参考《线性代数笔记(2):线性变换及其矩阵表示 》,线性变换T的rank定义为T的值域的维度,即rank(T)=dim(R(T))。下面我们来看看矩阵A的rank是如何定义的。
当然LA这种线性变换是比较特殊的,因为它相当于是输入一个n维的向量,输出一个m维的向量。对于一个更加一般的变换T,我们是否能将它的rank与对应矩阵表达的rank联系起来呢?下列定理给出了我们想要的答案。
得出这个结论并不意外,根据之前介绍的“同构”关系,就很容易得出这个结果。事实上我们还可以证明isomorphism具有rank-preserving的性质。也就是说,如果Φβ是一个isomorphism,V'是V的一个子空间,那么就有dim(V')=dim(Φβ(V'))。
关于rank-preserving的性质,还有如下结果,即矩阵A乘以一个可逆矩阵,那么它的rank不变。这也很容易解释,因为如果存在一个可逆的变换在T,我们其实就得到了一个isomorphism,而isomorphism是rank-preserving的,这样的作用当然不会改变rank。
此外,关于基本矩阵操作我们还有如下推论:Elementary row and column operations on a matrix are rank preserving.(因为基本矩阵操作都是invertible的)
四、由矩阵的形式直接判断其rank的方法
上述定理中的ai都表示一个列向量。所以这个定理就告诉我们一个矩阵的rank就等于它最大的“线性独立的列向量的”数量。
其中,Ir有是r行r列的单位矩阵。O1的大小为r×(n-r),O2的大小为(m-r)×r,O3的大小为(m-r)×(n-r)。
由此,我们还可以得到如下推论:
这个推论的得出也非常straightforward,你可以想象,定理3.6中,我们是如何从A得到D的。当对A做一个基本行运算或基本列运算时,等价的就相当于对其乘以一个“由相同基本变换”得到的基本矩阵,如下所示,注意到基本矩阵是可逆的,所以它们的连乘仍然可逆。所以得出这个结果也就非常自然了。
我们还可以得到下面这个推论(也就是说矩阵转置,rank不变):
Cor3. Every invertible matrix is a product of elementary matrices.
注意,如果A是可逆矩阵(所以它也是一个n×n的方阵),则rank(A)=n。这是因为A可逆,则LA也可逆,即LA是onto的,如果LA是满射的,则它的值域自然是n,即rank(LA)=n,也就得出了rank(A)=n的结果。
五、算子合成(或矩阵相乘)之后的rank小于原算子(或矩阵)的rank
六、矩阵的逆
如果A是n×n的可逆矩阵,那么by only using 基本行变换(or only using 基本列变换)运算,(A | I) 型的增广矩阵会变成(I | A-1),这也就是一般求解矩阵的逆的方法。
但是,如果A是不可以逆的,那么经过基本行(或列)运算,(A | I) 型的增广矩阵会变成(C | B),其中C中一定有一行全为0。
七、线性方程组
Def. Ax = b of m linear equations in n unknowns is said to be homogeneous(齐次的)if b = 0;相反,若 b ≠ 0,则称为nonhomogeneous(非齐次的)。
注意,上述LA: Fn→Fm。推论告诉我们,如果未知数的数量n大于方程的个数m,则齐次方程有非零解。
![]() (解的唯一性)
(解的唯一性)
Thm 3.11: The system Ax=b is consistent(有解) ⇔ rank(A) = rank(A | b),也就是说b∈Range(A). (解的存在性)
八、高斯消元法解方程组的相关内容
高斯消元法(略)
Thm 3.15:Let Ax = b be a system of r nonzero equations in n unknowns. Suppose that
1)rank(A|b) = rank(A) (注释:保证Ax = b有解)
2)(A|b) is in reduced row echelon form.
Then,
1)rank(A) = r;
2)the general solution s of Ax = b can be written as
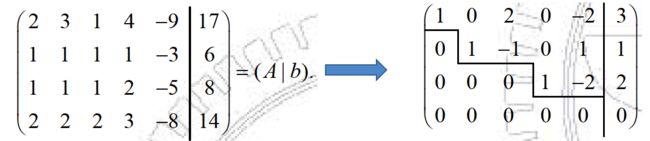
例:
(本文完)
本文主要根据台湾交通大学开放课程线性代数(莊重 特聘教授主讲)之授课内容整理,并参考以下书籍:
【1】S.H. Friedberg, A.J. Insel, L.E Spence, 4th edition, Linear Algebra, Prentice-Hall, 2003
【2】David C. Lay. 刘深泉,等译. 线性代数及其应用(原书第3版),机械工业出版社,2005