lua table的长度问题

细谈一下lua里很多人有疑问的table长度问题。

1.	> tbl = {1,2,3}  
	> print(#tbl)
	3
	> 
2.	> tbl = {1,nil,3}
	> print(#tbl)    
	3
	> 
3.	> tbl = {1,nil,3,nil}
	> print(#tbl)      
	1
	> 
 
  
 
  
 
  
 
  
 
  
 
  
情况1正常，情况2有点不正常，情况3很不正常，好，先上源码。
 
  
 
  
int luaH_getn (Table *t) {
  unsigned int j = t->sizearray;
  if (j > 0 && ttisnil(&t->array[j - 1])) {
    /* there is a boundary in the array part: (binary) search for it */
    unsigned int i = 0;
    while (j - i > 1) {
      unsigned int m = (i+j)/2;
      if (ttisnil(&t->array[m - 1])) j = m;
      else i = m;
    }
    return i;
  }
  /* else must find a boundary in hash part */
  else if (isdummy(t->node))  /* hash part is empty? */
    return j;  /* that is easy... */
  else return unbound_search(t, j);
}
 
  
 
  
 
  
此函数是用来求知table的长度，理解这个函数对于lua table的整个原理有很大帮助。
 
  
 
  
条件1：j>0而且数组部分最后一个为空，则进入下面的二分查找，此二分查找就是找到一个i不为空，j为空的的两个索引，当j-i>1就跳出来返回i.
 
  
条件2：j<=0或者数组最后一个不为空，而且没有hash部分，此时，没办法，没得统计，折中返回数组的长度的。
 
  
条件3：j<=0或者数组最后一个不为空，有hash部分，进入到unbound_search,从字面意思，就是在一个乱的区间查找,此函数最终也是一个二分查找。
 
  
先理解条件1，最上面的情况三就符合条件1的情形，好，直接上gdb.下面的截图，慢慢看。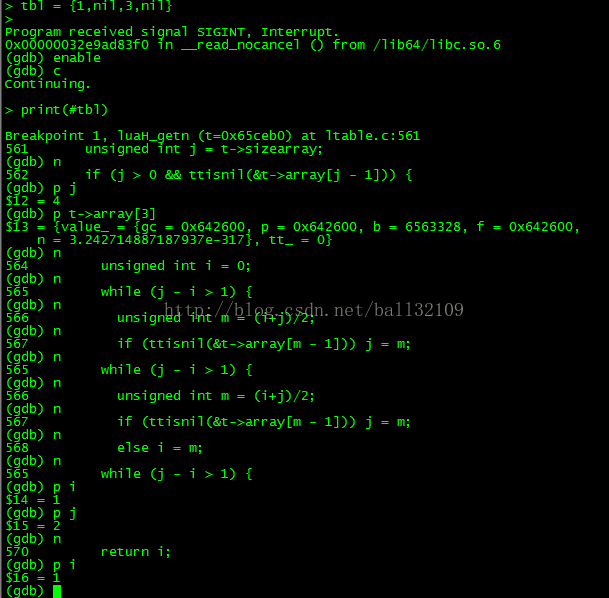
 
  
 
  
数组长度j = t->t->sizearray = 4,j>0,把最后一个元素打印出来：
 
   
  
 
  
 
  
tt_ = 0表示此元素为nil值，符合条件1，进入到二分查找，此二分查找就是找到一个左边不为nil,右边为nil时的左边索引。
 
  
i = 0,j = 4,m = (i+j)/2 = 2,m-1 = 1,索引为1的元索是nil,0才是1，所以j = m = 2;
 
  
i = 0,j = 2,m = (i+j)/2 = 1,m-1 = 0,索引为0的元索是1,所以i = m = 1;
 
  
i = 1,j=2,退出循环,长度为1.
 
  
 
 
  
可以得知，就算仅仅统计只有数组部分的长度也有可能不正常。
 
  
 
  
条件2制造很简单，跟情况2符合，看gdb:
 
   
  
 
  
tbl = {1,nil,3},此table度度j = t->sizearray = 3,最后一个元素tt_ = 3,n = 3,就表示此value为number类型,值为3,也就是tbl最后一个元素不为nil,t->node 而且isdummy,hash部分也为空，折中直接返回数组长度3.
 
  
先看unbound_search函数实现：
 
  
static int unbound_search (Table *t, unsigned int j) {
  unsigned int i = j;  /* i is zero or a present index */
  j++;
  /* find `i' and `j' such that i is present and j is not */
  while (!ttisnil(luaH_getint(t, j))) {
    i = j;
    j *= 2;
    if (j > cast(unsigned int, MAX_INT)) {  /* overflow? */
      /* table was built with bad purposes: resort to linear search */
      i = 1;
      while (!ttisnil(luaH_getint(t, i))) i++;
      return i - 1;
    }
  }
  /* now do a binary search between them */
  while (j - i > 1) {
    unsigned int m = (i+j)/2;
    if (ttisnil(luaH_getint(t, m))) j = m;
    else i = m;
  }
  return i;
}

const TValue *luaH_getint (Table *t, int key) {
  /* (1 <= key && key <= t->sizearray) */
  if (cast(unsigned int, key-1) < cast(unsigned int, t->sizearray))
    return &t->array[key-1];
  else {
    lua_Number nk = cast_num(key);
    Node *n = hashnum(t, nk);
    do {  /* check whether `key' is somewhere in the chain */
      if (ttisnumber(gkey(n)) && luai_numeq(nvalue(gkey(n)), nk))
        return gval(n);  /* that's it */
      else n = gnext(n);
    } while (n);
    return luaO_nilobject;
  }
}
 
  
 
  
此函数传入一个数组长度，也就是认为数组满了，才进入到此函数。
 
  
第一个while就是一直查找到一个j，而且以此j为key，不存在于table，包括数组部分和hash部分（luaH_getint的实现），侧退出第一个while,如果中途j>MAX_INT,没办法，此j已经好大了，只能resort to linear search了，就是转到线性查找，一个一个找到一个为空就返回I-1为table的长度。
 
  
 在第一个while找到j之后，此时i和j就是左边不为nil,右边为nil的两个值，在此两值之前再二分查找，查找到一个最小的左边不为nil，右边为nil的两个值，返回前者。
 
  
 好，制造此情况，看gdb:
 
   
  
 
  
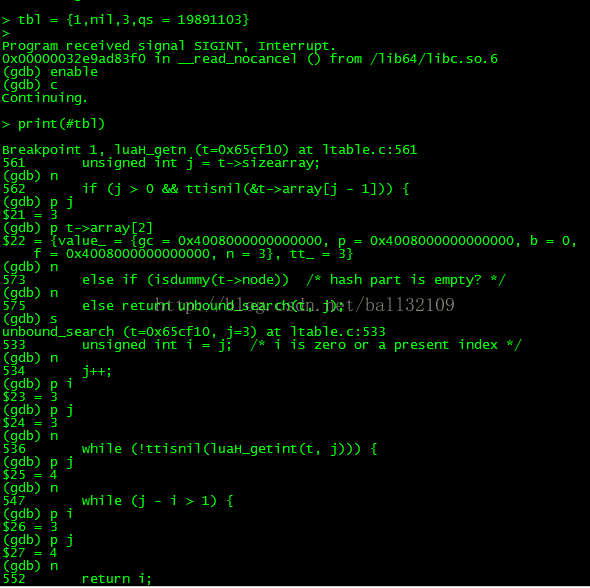
tbl = {1,nil,3,qs = 19891103},数组长度为3，最后一个元素不为nil,
 
  

 
  
 
  
有hash部分，见qs = 19891103,进入到一个杂乱无章的区间内查找(unbound_search),在进入第一个while时i=3,j=4,luaH_getint的时候
 
  
,以key为4在数组部分和hash部分都不存在的。直接进入到以左边为3，右边为4的二分查找(此二分查找上面有说)。直接就返回3为table的长度。
 
  
可见，进入到unbound_search的时候，此时获得数据长度，有可能靠谱，大部分情况都是不靠谱的。
 
  
如果数组部分是满的而且没有空洞情况，而且存在于hash部分的key跟数组部分是连续起来的，此时获取长度是达到预期的，有hash部分的时候就要进入到unbound_search查找，假如tbl = {1,2,3,[4] = 4},此时，对外来看，此tbl确实是一个数组，但在内存里，并不是，1,2,3在数组部分，4在hash部分，所以在进入unbound_search，此时获取长度也是正常的.