PCA主成分分析笔记
PCA主成分分析是用来做什么的?
主成分分析,是数据降维的一种方法,比如一件事,我们有 n n n个维度来描述它,但是这样描述起来太复杂,做数据处理的时候,也有计算量也很大。这时候,如果用较小的几个变量来说明这件事,就非常理想了。举个例子,在学习机器学习的时候,我看的第一本书是周志华的《机器学习》,里面经常用西瓜来举例,我这里也说一个西瓜的例子。比如,我们描述西瓜的时候,通常用色泽,根蒂,敲声,纹理,脐部,触感等来描述,这里一个瓜就要有6个变量,假设我们只想知道西瓜甜不甜,是大还是小,那么只需要两种描述方式就可以了。因此,我们可以列出

甜 度 = a 11 色 泽 + a 12 根 蒂 + a 13 敲 声 + a 14 纹 理 + a 15 脐 部 + a 16 触 感 个 头 = a 21 色 泽 + a 22 根 蒂 + a 23 敲 声 + a 24 纹 理 + a 25 脐 部 + a 26 触 感 \begin{aligned} 甜度=&a_{11}色泽+a_{12}根蒂+a_{13}敲声+a_{14}纹理+a_{15}脐部+a_{16}触感\\ 个头=&a_{21}色泽+a_{22}根蒂+a_{23}敲声+a_{24}纹理+a_{25}脐部+a_{26}触感 \end{aligned} 甜度=个头=a11色泽+a12根蒂+a13敲声+a14纹理+a15脐部+a16触感a21色泽+a22根蒂+a23敲声+a24纹理+a25脐部+a26触感
如此一来只需要两个变量(甜度、个头)就可以完成对西瓜的描述,起到了降维的作用。到这里我们也可以看到降维是保持对事物的描述基本不变的情况下,从 n n n维压缩到 m m m维( n > m n>m n>m)的过程。
如果觉得西瓜的例子不够形象,那么再举一个。我们从一张图上来看PCA到底可以起到什么作用.。
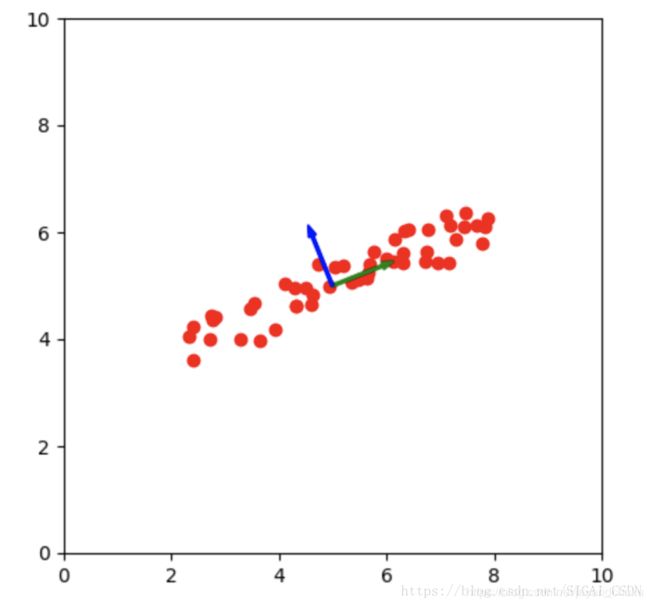
这张图来自理解主成分分析 (PCA),从图上我们可以看到,为了描述图中的红点,需要两个值,即横轴(假设为X),纵轴(假设为Y);我们又发现,图中的点呈现一种近乎于直线的排列。如果按图中绿、蓝轴重新建立坐标系,则图中的点,就可以近似的用绿轴( X 1 X_1 X1)一个值来表示,尽管不是特别精确,但是由于点在蓝轴上的坐标值差异不是很大,不太严格的情况下,可以看成是相等的,我们描述点的时候,只描述差异性的部分,也就是绿轴上的值就可以了。最开始描述一个点用两个值,通过改变坐标系(或坐标变换)后仅用一个值就可完成,这就是降维。
如何实现?
从西瓜的例子里,我们可以发现,降维后的描述是通过变量线性变换得到的。
我们从高惠璇老师的《应用多元统计分析》可以看到,假设有一个随机向量 X = { X 1 , X 2 , X 3 , … , X n } X=\{X_1,X_2,X_3,\ldots,X_n\} X={X1,X2,X3,…,Xn},均值 E ( x ) = μ E(x)=\mu E(x)=μ,方差 D ( X ) = Σ D(X)=\Sigma D(X)=Σ,这里根据方差的计算公式,可以得出 D ( X ) D(X) D(X)是个对称矩阵。新变量 Z i Z_i Zi为 X X X的一个线性组合,写成如下形式:
Z 1 = a 1 T X = a 11 X 1 + a 12 X 2 + a 13 X 3 + a 14 X 4 + ⋯ + a 1 n X n Z 2 = a 2 T X = a 21 X 1 + a 22 X 2 + a 23 X 3 + a 24 X 4 + ⋯ + a 2 n X n Z 3 = a 3 T X = a 31 X 1 + a 32 X 2 + a 33 X 3 + a 34 X 4 + ⋯ + a 3 n X n ⋯ Z m = a m T X = a m 1 X 1 + a m 2 X 2 + a m 3 X 3 + a m 4 X 4 + ⋯ + a m n X n \begin{aligned} Z_1=&a_1^TX=a_{11}X_1+a_{12}X_2+a_{13}X_3+a_{14}X_4+{\cdots}+a_{1n}X_n\\ Z_2=&a_2^TX=a_{21}X_1+a_{22}X_2+a_{23}X_3+a_{24}X_4+{\cdots}+a_{2n}X_n\\ Z_3=&a_3^TX=a_{31}X_1+a_{32}X_2+a_{33}X_3+a_{34}X_4+{\cdots}+a_{3n}X_n\\ &{\cdots}\\ Z_m=&a_m^TX=a_{m1}X_1+a_{m2}X_2+a_{m3}X_3+a_{m4}X_4+{\cdots}+a_{mn}X_n \end{aligned} Z1=Z2=Z3=Zm=a1TX=a11X1+a12X2+a13X3+a14X4+⋯+a1nXna2TX=a21X1+a22X2+a23X3+a24X4+⋯+a2nXna3TX=a31X1+a32X2+a33X3+a34X4+⋯+a3nXn⋯amTX=am1X1+am2X2+am3X3+am4X4+⋯+amnXn
由于 D ( X ) = Σ = E [ ( X − E ( X ) ) ( X − E ( X ) ) T ] D(X)=\Sigma=E[(X-E(X))(X-E(X))^T] D(X)=Σ=E[(X−E(X))(X−E(X))T],所以
V a r ( Z i ) = E [ ( Z i − E ( Z i ) ) ( Z i − E ( Z i ) ) T ] = E [ ( a i T X − a i T X ) ( a i T X − a i T X ) T ] = a i T E [ ( X − E ( X ) ) ( X − E ( X ) ) T ] a i = a i T Σ a i \begin{aligned} Var(Z_i)=&E[(Z_i-E(Z_i))(Z_i-E(Z_i))^T]\\ =&E[(a_i^TX-a_i^TX)(a_i^TX-a_i^TX)^T]\\ =&a_i^TE[(X-E(X))(X-E(X))^T]a_i\\ =&a_i^T{\Sigma}a_i \end{aligned} Var(Zi)====E[(Zi−E(Zi))(Zi−E(Zi))T]E[(aiTX−aiTX)(aiTX−aiTX)T]aiTE[(X−E(X))(X−E(X))T]aiaiTΣai
可以得到 Z i Z_i Zi的方差,为 V a r ( Z i ) = a i T Σ a i Var(Z_i)=a_i^T{\Sigma}a_i Var(Zi)=aiTΣai,同理,协方差 C o v ( Z i , Z j ) = a i T Σ a j Cov(Z_i,Z_j)=a_i^T{\Sigma}a_j Cov(Zi,Zj)=aiTΣaj。我们希望用 Z 1 Z_1 Z1代替原来的 n n n个变量 X 1 , X 2 , X 3 , … , X n X_1,X_2,X_3,\ldots,X_n X1,X2,X3,…,Xn,这就要求其能尽可能多的反映原来 n n n个变量的信息。信息的多少,我们用方差来度量。信息多的时候,以为着各个变量的值差异性较大,反之则差异性很小。这里我们再举个例子,如果有 n n n个西瓜,无论从色泽,根蒂,纹理等方面都是一样的,那么我用一个西瓜表示这一排西瓜就好,我们描述的信息就会非常少,只描述一个就好。如果各个西瓜差异比较大,那么就要分别描述每一个,因此包含的信息量就大,对应的是各项信息方差就大。因此方差是对信息量复杂程度的一个度量。
我们期望用最少的变量描述尽可能多的性质,那么每个变量所应包含的方差,应该是尽可能大的,而且变量间包含的内容不应有交叉。基于这样的原因,我们在寻找替代变量时,都是从所有变量中依次找到方差最大的那个,这里,包含信息最大的那个变量,就叫做第一主成分,第二、三主成分依次类推。
从 V a r ( Z i ) = a i T Σ a i Var(Z_i)=a_i^T{\Sigma}a_i Var(Zi)=aiTΣai来看,如果对 a i a_i ai不加限制,那么 V a r ( Z i ) Var(Z_i) Var(Zi)可以无限大,所以,常用的限制是 a i T a i = 1 a_i^Ta_i=1 aiTai=1。为什么限制是1呢,是因为,当 Σ \Sigma Σ是 n n n阶实对称矩阵的时候,假设它的特征值从大到小排列是 λ 1 , λ 2 , ⋯ , λ n \lambda_1,\lambda_2,\cdots,\lambda_n λ1,λ2,⋯,λn,对任一不为0的向量 a a a,存在如下关系 λ n ≤ a T Σ a a T a ≤ λ 1 \lambda_n\leq \frac{a^T\Sigma a}{a^Ta}\leq \lambda_1 λn≤aTaaTΣa≤λ1
当我们将 a i T a i a_i^Ta_i aiTai限制为1的时候,可以发现 λ n ≤ a T Σ a ≤ λ 1 \lambda_n\leq a^T\Sigma a\leq \lambda_1 λn≤aTΣa≤λ1,也就是 V a r ( Z i ) Var(Z_i) Var(Zi)的大小可以限定在方差的最大和最小特征值之间。这样简化了后续求主成分的计算。从这个公式也可以看出,第一主成分 Z i Z_i Zi的方差的最大值就是 λ 1 \lambda_1 λ1。因此问题就转化成在求一线性变换 a 1 a_1 a1,使得 (1) a 1 T Σ a 1 = λ 1 a_1^T{\Sigma}a_1=\lambda_1 \tag 1 a1TΣa1=λ1(1)。而第一主成分 Z 1 = a 1 T X Z_1=a_1^TX Z1=a1TX。
利用 a i T a i = 1 a_i^Ta_i=1 aiTai=1,对公式(1)进行变形,得到: Σ a 1 = λ 1 a 1 {\Sigma}a_1=\lambda_1 a_1 Σa1=λ1a1,到这里,发现实际上我们要求的 a 1 a_1 a1就是矩阵 Σ \Sigma Σ的关于特征值 λ 1 \lambda_1 λ1的特征向量。
当第一个主成分 Z 1 Z_1 Z1不能完全表示所有信息时,需要继续计算第二个主成分 Z 2 Z_2 Z2。因为 Z 2 Z_2 Z2不应该包含 Z 1 Z_1 Z1中的信息,所以 Z 2 Z_2 Z2与 Z 1 Z_1 Z1是正交关系。假设 ξ i \xi_i ξi是属于 Σ \Sigma Σ的特征值 λ i \lambda_i λi的特征向量,记 L 1 = L ( ξ 1 , ξ 2 , … , ξ n ) L_1=L(\xi_1,\xi_2,\ldots,\xi_n) L1=L(ξ1,ξ2,…,ξn),即 L 1 L_1 L1为 ξ i ( i = 1 , 2 , … , n ) \xi_i(i=1,2,\ldots,n) ξi(i=1,2,…,n)张成的空间。当求出第一个主成分 Z 1 Z_1 Z1后,其余成分在 L 2 ( ξ 2 , ξ 3 , … , ξ n ) L_2(\xi_2,\xi_3,\ldots,\xi_n) L2(ξ2,ξ3,…,ξn)中查找。同第一主成分一样,可以得到第二主成分 Z 2 Z_2 Z2, V a r ( Z 2 ) = λ 2 Var(Z_2)=\lambda_2 Var(Z2)=λ2。按此,可以求出其余主成分。
需要注意的地方
通过对降维的手段分析,它仅仅是对原有维度的一次线性变换。它也有自身的缺点,如:
1) 如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高;
2) 特征值分解有一些局限性,比如变换的矩阵必须是方阵;
3) 在非高斯分布情况下,PCA方法得出的主元可能并不是最优的。
对PCA缺点的描述,来自于人工智能算法最全汇总之PCA算法