Java数据结构和算法——数组、单向链表、双向链表

概要

线性表是一种线性结构，它是具有相同类型的n(n≥0)个数据元素组成的有限序列。本文先介绍线性表的几个基本组成部分：数组、单向链表（One-way LinkedList）、双向链表（two-way linked-list ）。

数组

数组有上界和下界，数组的元素在上下界内是连续的。

存储10、20、30、40、50的数组的示意图如下：

数组的特点：
1. 数据是连续的；
2. 随机访问速度快。

数组中稍微复杂一点的是多维数组和动态数组。

对于C语言来说，多维数组本质上是通过一维数组实现的，至于动态数组，是指数组的容量能动态增长的数组。

C语言实现动态数组需要手动实现，而对于C++而言，STL提供了Vector，对于Java语言而言，Collection集合则提供了ArrayList和Vector。

单向链表

单向链表（单链表）是链表的一种，它由节点组成，每个节点都包含下一个节点的指针。

单链表的示意图如下：

表头为空，表头的后继节点是”节点10”(数据为10的节点)，”节点10”的后继节点是”节点20”(数据为20的节点)，…

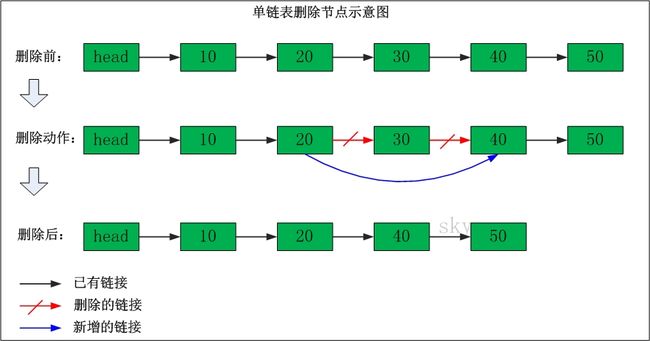
单链表删除节点

删除”节点30”

删除之前：”节点20” 的后继节点为”节点30”，而”节点30” 的后继节点为”节点40”。
删除之后：”节点20” 的后继节点为”节点40”。

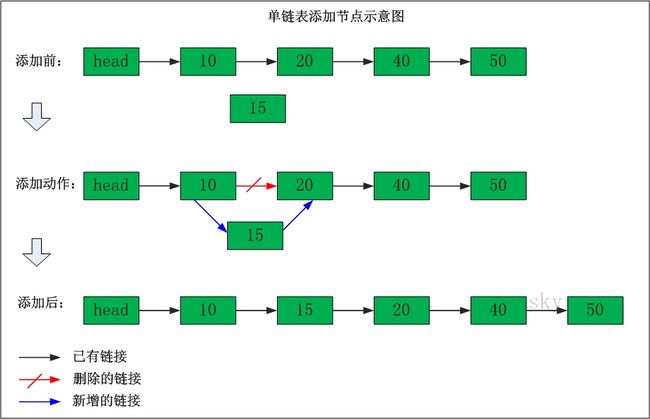
单链表添加节点

在”节点10”与”节点20”之间添加”节点15”

添加之前：”节点10” 的后继节点为”节点20”。
添加之后：”节点10” 的后继节点为”节点15”，而”节点15” 的后继节点为”节点20”。

单链表特点

1. 节点的链接方向是单向的；
2. 与数组比较，单链表随机访问速度较慢，但是单链表删除和添加数据的效率很高。

双向链表

双向链表（双链表）也是链表的一种，和单链表一样，双链表也是由节点组成，他的每个数据节点都有两个指针，分别指向直接后继和直接前驱。所以，从双向链表的任何一个节点开始，都能方便的访问它的前驱节点和后继节点。一般我们都构造双向循环链表。

双链表的示意图如下：

表头为空，表头的后继节点为”节点10”(数据为10的节点)；”节点10”的后继节点是”节点20”(数据为20的节点)，”节点20”的前继节点是”节点10”；”节点20”的后继节点是”节点30”，”节点30”的前继节点是”节点20”；…；末尾节点的后继节点是表头。

双链表删除节点

删除”节点30”

删除之前：”节点20”的后继节点为”节点30”，”节点30” 的前继节点为”节点20”。”节点30”的后继节点为”节点40”，”节点40” 的前继节点为”节点30”。
删除之后：”节点20”的后继节点为”节点40”，”节点40” 的前继节点为”节点20”。

双链表添加节点

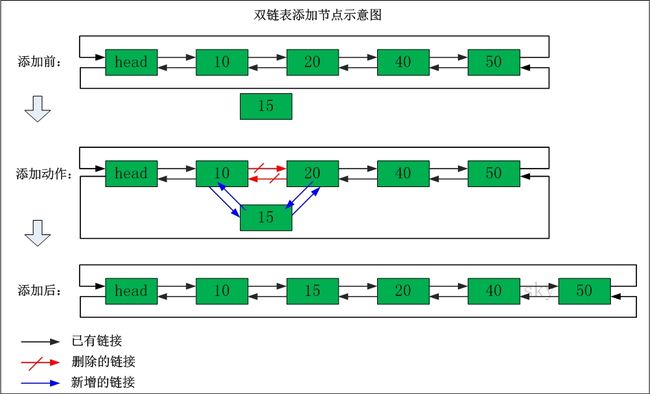
在”节点10”与”节点20”之间添加”节点15”

添加之前：”节点10”的后继节点为”节点20”，”节点20” 的前继节点为”节点10”。
添加之后：”节点10”的后继节点为”节点15”，”节点15” 的前继节点为”节点10”。”节点15”的后继节点为”节点20”，”节点20” 的前继节点为”节点15”。

---

Java实现双链表

双链表类(DoubleLink.java)

package com.qq.main;

public class DoubleLink {

    private DNode mHead;
    private int mCount;

    // 双向链表“节点”对应的结构体
    private class DNode {
        public DNode prev;
        public DNode next;
        public T value;

        public DNode(T value, DNode prev, DNode next) {
            this.value = value;
            this.prev = prev;
            this.next = next;
        }
    }

    public DoubleLink() {
        // 创建“表头”。注意：表头没有存储数据！
        mHead = new DNode(null, null, null);
        mHead.prev = mHead.next = mHead;
        // 初始化“节点个数”为0
        mCount = 0;
    }

    // 返回节点数目
    public int size() {
        return mCount;
    }

    public boolean isEmpty() {
        return mCount == 0;
    }

    // 获取第index位置的节点
    public DNode getNode(int index) {
        if (index < 0 || index >= mCount)
            throw new IndexOutOfBoundsException();

        // 正向查找
        if (index <= mCount / 2) {
            DNode node = mHead.next;// 获取第一个节点，从第一个节点开始
            for (int i = 0; i < index; i++) {
                node = node.next;
            }
            return node;
        }

        // 反向查找
        DNode rnode = mHead.prev;
        int rindex = mCount - index - 1;
        for (int i = 0; i < rindex; i++) {
            rnode = rnode.prev;
        }

        return rnode;
    }

    // 获取第index位置的节点的值
    public T get(int index) {
        return getNode(index).value;
    }

    // 获取第1个节点的值
    public T getFirst(int index) {
        return getNode(0).value;
    }

    // 获取最后一个节点的值
    public T getLast(int index) {
        return getNode(mCount - 1).value;
    }

    // 将节点插入到第index位置之前
    public void insert(int index, T t) {
        if (0 == index) {
            DNode node = new DNode(t, mHead, mHead.next);
            mHead.next.prev = node;
            mHead.next = node;
            mCount++;
        } else {
            DNode node = getNode(index);
            DNode tNode = new DNode(t, node.prev, node);
            node.prev.next = tNode;
            node.next = tNode;
            mCount++;
        }

    }

    // 将节点插入第一个节点处
    public void insertFirst(T t) {
        insert(0, t);
    }

    // 删除index位置的节点
    public void delete(int index) {
        DNode node = getNode(index);
        node.prev.next = node.next;
        node.next.prev = node.prev;
        node = null;
        mCount--;
    }

    // 删除第一个节点
    public void deleteFirst() {
        delete(0);
    }

    // 删除最后一个节点
    public void deleteLast() {
        delete(mCount - 1);
    }

    // 将节点追加到链表的末尾
    public void appendLast(T t) {
        DNode node = new DNode(t, mHead.prev, mHead);
        mHead.prev.next = node;
        mHead.prev = node;
        mCount++;
    }

}

测试：

public class DlinkTest {

    public static void main(String[] args) {
        int_test();
        string_test();
        object_test();

    }

    // 双向链表操作int数据
    private static void int_test() {
        int[] iarr = { 10, 20, 30, 40 };

        System.out.println("\n----int_test----");
        // 创建双向链表
        DoubleLink dlink = new DoubleLink();

        dlink.insert(0, 20); // 将 20 插入到第一个位置
        dlink.appendLast(10); // 将 10 追加到链表末尾
        dlink.insertFirst(30); // 将 30 插入到第一个位置

        // 双向链表是否为空
        System.out.printf("isEmpty()=%b\n", dlink.isEmpty());
        // 双向链表的大小
        System.out.printf("size()=%d\n", dlink.size());

        // 打印出全部的节点
        for (int i = 0; i < dlink.size(); i++)
            System.out.println("dlink(" + i + ")=" + dlink.get(i));
    }

    private static void string_test() {
        String[] sarr = { "ten", "twenty", "thirty", "forty" };

        System.out.println("\n----string_test----");
        // 创建双向链表
        DoubleLink dlink = new DoubleLink();

        dlink.insert(0, sarr[1]); // 将 sarr中第2个元素 插入到第一个位置
        dlink.appendLast(sarr[0]); // 将 sarr中第1个元素 追加到链表末尾
        dlink.insertFirst(sarr[2]); // 将 sarr中第3个元素 插入到第一个位置

        // 双向链表是否为空
        System.out.printf("isEmpty()=%b\n", dlink.isEmpty());
        // 双向链表的大小
        System.out.printf("size()=%d\n", dlink.size());

        // 打印出全部的节点
        for (int i = 0; i < dlink.size(); i++)
            System.out.println("dlink(" + i + ")=" + dlink.get(i));
    }

    private static void object_test() {
        System.out.println("\n----object_test----");
        // 创建双向链表
        DoubleLink dlink = new DoubleLink();

        dlink.insert(0, students[1]); // 将 students中第2个元素 插入到第一个位置
        dlink.appendLast(students[0]); // 将 students中第1个元素 追加到链表末尾
        dlink.insertFirst(students[2]); // 将 students中第3个元素 插入到第一个位置

        // 双向链表是否为空
        System.out.printf("isEmpty()=%b\n", dlink.isEmpty());
        // 双向链表的大小
        System.out.printf("size()=%d\n", dlink.size());

        // 打印出全部的节点
        for (int i = 0; i < dlink.size(); i++) {
            System.out.println("dlink(" + i + ")=" + dlink.get(i));
        }
    }

    // 内部类
    private static class Student {
        private int id;
        private String name;

        public Student(int id, String name) {
            this.id = id;
            this.name = name;
        }

        @Override
        public String toString() {
            return "[" + id + ", " + name + "]";
        }
    }

    private static Student[] students = new Student[] { 
            new Student(10, "sky"), 
            new Student(20, "jody"),
            new Student(30, "vic"), 
            new Student(40, "dan"), 
            };
}

运行输出结果如下：

----int_test----
isEmpty()=false
size()=3
dlink(0)=30
dlink(1)=20
dlink(2)=10

----string_test----
isEmpty()=false
size()=3
dlink(0)=thirty
dlink(1)=twenty
dlink(2)=ten

----object_test----
isEmpty()=false
size()=3
dlink(0)=[30, vic]
dlink(1)=[20, jody]
dlink(2)=[10, sky]

每天进步一点点！

C和C++实现双链表的实现，请移步：
http://www.cnblogs.com/skywang12345/p/3561803.html

本文是对上面博客的学习和记录，更详细讲解请访问该博客。

2016.6.26 完成学习记录。