Trie的实现

首先要说下什么是trie，比如在string中搜索pattern

在banana中搜索“ban", “ana”, "nab"这几个pattern，那么就需要一次一个pattern地搜，但是在pattern很多的时候复杂度就会是O(average pattern.lengthpattern numtext.length)

trie就是把很多string pattern整合在一起，然后搜索的时候可以减掉pattern num这一项

比如ba和bb，组合成

因此在baabb中搜索ba和bb时，可以通过一个trie一次满足

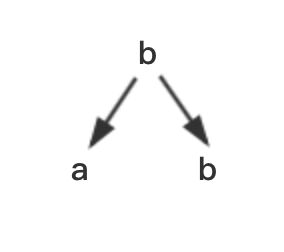
如果在上述trie中再insert一个b，trie会变成

这时候说下search，search有full search和prefix search，就是完全相同，或者是否以pattern开头。如果是完全相同方式搜索，当搜索ba时，会走bab路径，这时候如何判断ba是一个完整的字符串，还是bab的一部分？就需要一个boolean值endOfWord来判断，endOfWord=true时，就知道a已经是子字符串的终点。

所以定义TrieNode结构，需要包含一个指向下一节点的TrieNode指针，和一个endOfWord的boolean值。因为可能有多个children，所以用Map来定义children。

class TrieNode{
    Map children;
    boolean endOfWord;
    
    public TrieNode(){
        children = new HashMap<>();
        endOfWord = false;
    }
}

插入操作时，先看当前字母在trie中是否存在，如果存在，走向它的下一节点，如果不存在，建立新的TrieNode。当走到最后一个字母时，endOfWord设为 true

    public void insert(String word) {
        char ch = 0;
        TrieNode current = root;
        TrieNode node;
        
        for(int i = 0; i < word.length(); i++) {
            ch = word.charAt(i);
            node = current.children.get(ch);
            if(node == null) {
                node = new TrieNode();
                current.children.put(ch, node);
            }
            current = node;
        }
        current.endOfWord = true;
    }

新建一个Trie时，只需建立一个root和它的一个空children

    private final TrieNode root;
    
    public Trie() {
        root = new TrieNode();
    }

完全搜索和前缀搜索的区别只是走到最后一个字母时，看endOfWord是否为true

    public boolean search(String word) {
        char ch = 0;
        TrieNode current = root;
        TrieNode node;
        
        for(int i = 0; i < word.length(); i++) {
            ch = word.charAt(i);
            node = current.children.get(ch);
            if(node == null) {
                return false;
            }
            current = node;
        }
        if(!current.endOfWord) {
            return false;
        }
        return true;
    }

    public boolean startsWith(String prefix) {
        char ch = 0;
        TrieNode current = root;
        TrieNode node;
        
        for(int i = 0; i < prefix.length(); i++) {
            ch = prefix.charAt(i);
            node = current.children.get(ch);
            if(node == null) {
                return false;
            }
            current = node;
        }
        
        return true;
    }
}