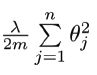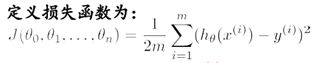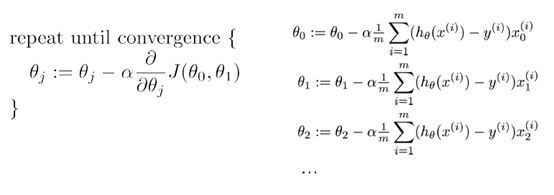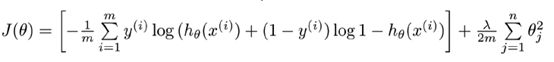一、理论篇
LR回归包括两个:Linear
Regression(线性回归),Logistic Regression(逻辑回归)。对回归来说,梯度下降法是最基础的算法了:
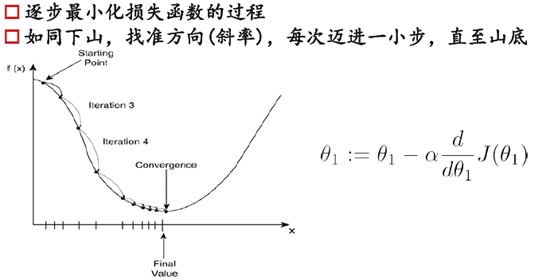
选定损失函数(衡量回归效果的好坏,值越小归回的越好),求偏导,梯度下降,迭代求得损失函数的极小值,就完成了回归。
梯度下降有个局限,只有凸函数才可以使用。
线性回归和逻辑回归的区别便是损失函数的选取不同,但它们的损失函数都是凸函数。
当然有个值得注意的地方,如果参数过多,可能会出现过拟合的情况,需要在损失函数后面加上一个正则项,控制参数的个数,然后回归曲线尽量光滑。
1.线性回归
线性回归比较简单,高中就学过用最小二乘法求解。
现在有工具了,可以利用计算机,当然不再像高中那般用笔算了。
线性回归的损失函数在这不做讨论,太简单。
对它求偏导J’,选定一个步长a
这样不断迭代,自然就走到最低点了。
2.逻辑回归
为什么要逻辑回归?
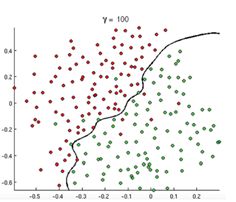
现实中有很多数据是只有两种情况的,要么0要么1.比如得还是不得癌症,比如淘宝上某个商品点击还是不点击。那这个时候我们要预测它是0还是1,就不能使用线性回归。我们需要的只是一个边界,边界的这边是0,那边是1.比如下图:
那么,怎样判定边界呢?
也可以像线性回归那样找一个损失函数,求损失函数的极小值就好了。
上上周看到的是这个版本,由于没有推到过程,虽然对它求导、梯度下降,结果也是一样的,但我必须要知道它是怎么来的!
于是又花了一周的时间去折腾。
以下是逻辑回归理论推导过程:
二、实现篇
'''
Created on 2017年6月18日
@author:fujianfei
'''
fromnumpyimport*
importmatplotlib.pyplotasplt
fromos.pathimportos
frommatplotlib.pyplotimportscatter,legend,show
fromsympy.solvers.solversimportsolve
#定义sigmoid函数
defsigmoid(inX):
return1.0/ (1+ exp(-inX))
#计算L的偏导
defLogDerivative(X,y,theta):
logD=sum((y-sigmoid(X.dot(theta)))*X,axis=0)#对列求和
logD=reshape(logD,(len(theta),1))
returnlogD
#梯度下降
defLogGradientDesc(X,y,theta=ones((3,1)),alpha=.001,iterations=200):
fornumberinrange(iterations):
theta = theta +alpha*LogDerivative(X,y,theta)
returntheta
#拟合效果,你拟合精度
deftestLogRegres(weights, test_x, test_y):
numSamples,numFeatures=shape(test_x)
matchCount =0
foriinrange(numSamples):
predict = sigmoid(test_x[i,:].dot(weights)) >0.5
ifpredict == bool(test_y[i,0]):
matchCount +=1
accuracy = float(matchCount) /numSamples
returnaccuracy
#画图
defshowLogRegres(weights, train_x, train_y):
numSamples, numFeatures =shape(train_x)
ifnumFeatures !=3:
print('Sorry! I can not draw because the dimension of your data is not 2!')
return1
foriinrange(numSamples):
ifint(train_y[i,0]) ==0:
plt.plot(train_x[i,1], train_x[i,2],'or')
elifint(train_y[i,0]) ==1:
plt.plot(train_x[i,1], train_x[i,2],'ob')
min_x = min(train_x[:,1])
max_x = max(train_x[:,1])
y_min_x = float(-weights[0] - weights[1] * min_x) / weights[2]
y_max_x = float(-weights[0] - weights[1] * max_x) / weights[2]
plt.plot([min_x, max_x], [y_min_x,y_max_x],'-g')
plt.xlabel('X1'); plt.ylabel('X2')
plt.show()
#实现
if__name__ =='__main__':
data_path = os.getcwd()+'\\data\\'
'''
逻辑斯特回归,线性决策边界
'''
#读取数据
print("step 1:
loading the data...")
logisticDate = loadtxt(data_path+'data1.txt',delimiter=',')
X=logisticDate[:,0:2]
mapped_fea=map_feature(X[:,0],X[:,1])
m,n=mapped_fea.shape
#meanVal=mean(X,axis=0)
#X=X-meanVal
xone=ones((len(X),1))
X=column_stack([xone,X])#在X上加一列常数,数值为1 theta0
y=logisticDate[:,2]
y=reshape(y,(len(y),1))
print("step 2:
training the data...")
theta=LogGradientDesc(X,y)
print(theta)
print("step 3:
testing the result...")
accuracy = testLogRegres(theta, X, y)
print(accuracy)
print("step 4:
show the result...")
showLogRegres(theta, X, y)
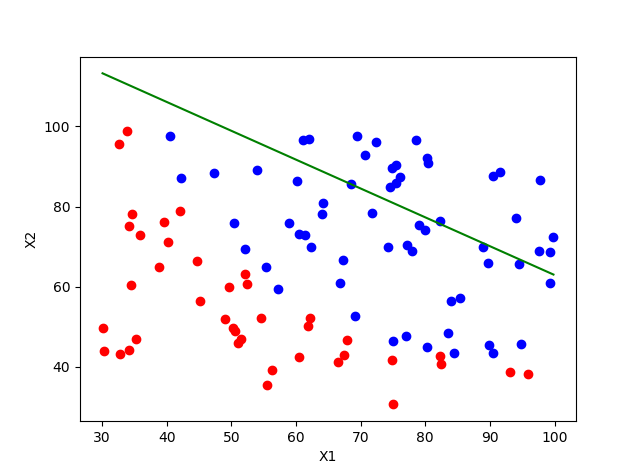
图1是一组原本就是零均值的数据的结果,也是我第一次做出来的效果,初始值1,步长0.01,迭代次数200:
换了一组不是零均值化的数据后,初始值1,步长0.01,迭代次数200,明显效果不对,初始值和步长都选错了:
然后我换了初始值和步长,初始值为10,步长0.00001,迭代20000:
最后我懒得猜初始值和步长了.直接零均值化,初始值1,步长0.01,迭代次数200:
三、问题篇
1.选步长和初始值很重要,为了好选,是否可以将数据进行零均值化?
2.以上分析都是线性决策边界,我试图做出非线性决策边界,将x1,x2以多项式组合起来,然后再加上不同的参数,结果并不理想,精度只有0.53,加上python技术有限,画不来这个多项式组合后的图形,看不见具体的效果,这个问题先留着,下次看到相关资料再细究。
#多项式特征组合
defmap_feature(x1,x2):
x1.shape = (x1.size,1)
x2.shape = (x2.size,1)
degree=6
mapped_fea = ones(shape=(x1[:,0].size,1))
foriinrange(degree +1):
forjinrange (i+1):
r=(x1 ** (i - j))*(x2 ** j)
mapped_fea = append(mapped_fea, r,axis=1)
returnmapped_fea
3.如果结束迭代的条件不是迭代次数,而是偏导值小于某个下限,是否也可以?为什么在网上没看见有人这样做过.
4.我用的是最笨的迭代方式,梯度下降,还有一些优化的迭代方式。
四、总结
逻辑回归原理:通过最大似然求出L,再对L求偏导,最后迭代。
真正开始搞逻辑回归是上周天,认真搞了一天,本周一到周五白天上班,晚上回来也就查个漏补个缺,本篇文章肯定漏洞百出,加之昨晚几乎没睡,如今没有精力去深究了,先往前看看,看的风景多了,自然就知道以前缺什么了。
参考:
http://blog.csdn.net/zouxy09/article/details/20319673
P`��?��