Trie 树构造原理、应用场景与复杂度分析

Trie 树构造原理

字典树，又称 Trie 树，是一种专门用于字符串匹配的树形结构，能够高效的在一组字符串中寻找所求字符串，与红黑树，散列表类似，但是又有其优势。

如何构造一颗 Trie 树
假设我们有一组字符串：abc，adf，adrf，siab。
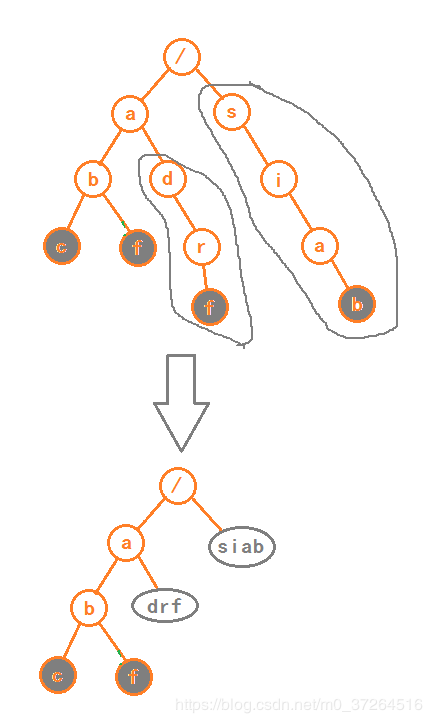
Trie 树的本质，就是利用字符串之间的公共前缀，将重复的前缀合并在一起。如图：

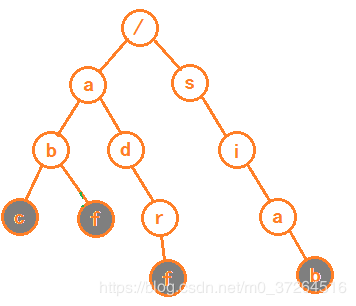
根节点不包含任何信息，从根节点一路往下到灰色节点，便是一个字符串。

注意：灰色节点并不一定是叶子节点，当字符串组中存在abc，abcdfg这样的时，前者是后者的前缀，为了区分是两个字符串，需要给每个字符串的结尾字符做标记。

在Trie树中查找
假设我们要查找abf，先将其拆分成 单个字符，按照下图路径，一层一层比较查找。直到最后一个字符恰好存在并且是灰色节点。

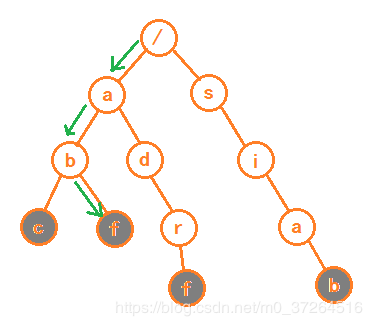
如何构造一颗 Trie 树
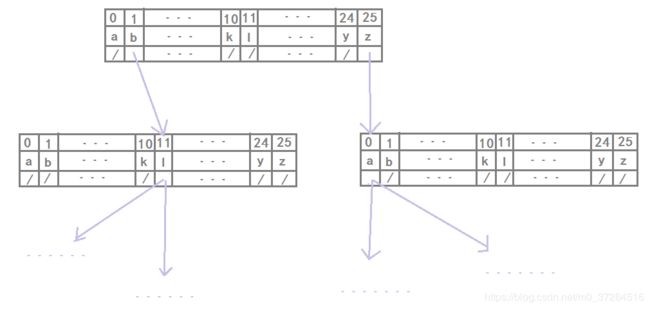
上述分析可知，字典树是一颗多叉树，二叉树中是通过左右子节点指针实现的，那么多叉树该如何实现呢？

//二叉树
class BinaryTreeNode{
	char data;
	BinaryTreeNode left;//左子节点
	BinaryTreeNode right;//右子节点
}

假设当前字符串只包含a-z 26 个字符，那么可以使用 26 个单位的子节点数组来实现：

class TriaTree{
	char data;
	bool isEndingChar;
	TriaTree node[26];
}

//字典树单个节点类
public class TriaTree {
    public char data;//数据域
    public TriaTree[] children = new TriaTree[26];//指向下一个字符
    public boolean isEndingChar = false;//是否为某个字符串结尾字符
    
    public TriaTree(char data) {
        this.data = data;
    }
}

public class Trie {
    private TriaTree root = new TriaTree('/'); // 存储无意义字符

    // 往 Trie 树中插入一个字符串
    public void insert(char[] str) {
        TriaTree p = root;
        for (int i = 0; i < str.length; ++i) {
            int index = str[i] - 'a';
            if (p.children[index] == null) {
                TriaTree newNode = new TriaTree(text[i]);
                p.children[index] = newNode;
            }
            p = p.children[index];
        }
        p.isEndingChar = true;
    }

    // 在 Trie 树中查找一个字符串
    public boolean find(char[] pattern) {
        TriaTree p = root;
        for (int i = 0; i < pattern.length; ++i) {
            int index = pattern[i] - 'a';
            if (p.children[index] == null) {
                return false; // 不存在 pattern
            }
            p = p.children[index];
        }
        return p.isEndingChar;
    }
}

复杂度分析

时间复杂度：
假设所有字符串长度之和为n，构建字典树的时间复杂度为O(n)
假设要查找的字符串长度为k，查找的时间复杂度为O(k)

空间复杂度：
字典树每个节点都需要用一个数组来存储子节点的指针，即便实际只有两三个子节点，但依然需要一个完整大小的数组。所以，字典树比较耗内存，空间复杂度较高。

如何优化？

1. 可以牺牲一点查询的效率，将每个节点的子节点数组用其他数据结构代替，例如有序数组，红黑树，散列表等
   例如，当子节点数组采用有序数组时，可以使用二分查找来查找下一个字符。

2. 缩点优化
   将末尾一些只有一个子节点的节点，可以进行合并，但是增加了编码的难度。如图
   

字典树与散列表红黑树的比较

字典树的缺陷：

1. 需要处理的字符串的字符集不能过大，否则存储空间过于浪费，即便是采用优化方案，也是在牺牲部分查询性能的基础上的
2. 在字符串前缀重合较多的情况，才有比较好的性能表现
3. 没有现成的字典树可以用，如果要使用需要手写，
4. 字典树中使用到了指针，因此前后节点是不连续的，对 CPU 缓存不友好

综上：在字符串的精确查找场景中，推荐使用红黑树，散列表等数据结构。

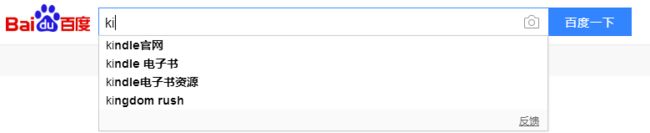
而字典树，则适合在查找前缀的场景下，例如，搜索引擎一般在输入部分字符后，会显示一些预选关键字。这些关键字均是以输入的字符为前缀。