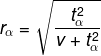直线回归和相关------（四）直线相关系数和决定系数（原理与公式推导）
一、相关系数
对于坐标点呈直线趋势的两个变数，如果并不需要由X来估计Y，而仅需了解X和Y是否确有相关以及相关的性质（正相关或负相关），则首先应算出表示X和Y 相关密切程度及其性质的统计数 —— 相关系数。一般以 
表示总体相关系数，r表示样本相关系数。
设有一X,Y均为随机变量的双变数总体，具有N对（X,Y）。若在标有这N个（X,Y）坐标点的直角坐标平面上移动坐标轴，将X轴和Y轴分别平移到 
和 
上，则各个点的位置不变，而所取坐标变为（X-,Y-）。
在象限Ⅰ， （X-）>0,（Y-）>0;在象限 Ⅱ， （X-）<0,（Y-）>0;
在象限Ⅲ， （X-）<0,（Y-）<0;在象限 Ⅳ， （X-）>0,（Y-）<0;
(X,Y)总体呈正相关时，落在象限 Ⅰ，Ⅲ的点一定比落在 象限 Ⅱ，Ⅳ 的多，
一定为正；
同时落在象限 Ⅰ，Ⅲ的点所占的比率愈大，此正值愈大。
(X,Y)总体呈负相关时，落在象限 Ⅱ，Ⅳ 的点一定比落在 象限 Ⅰ，Ⅲ 的多，一定为负 ；
同时落在象限 Ⅱ，Ⅳ 的点所占的比率愈大，此负值愈大；
(X,Y)总体无相关，则落在Ⅰ，Ⅱ，Ⅲ，Ⅳ的点是均匀分散的，正负相消，=0
以上说明，的值可用来度量两个变数直线相关的相关程度和性质。但，X和Y 的变异程度、所取单位以及N 的大小都会影响，为便于普遍应用，应消去这些因素的影响。
消去方法：将离均差转换成以各自的标准差单位，使成为标准化离差，再以N除之。
双变数总体的相关系数
为：
![\rho =\frac{1}{N}\sum_{1}^{N} [(\frac{X-\mu _{X}}{\sigma _{X}})(\frac{Y-\mu _{Y}}{\sigma _{Y}})]](http://img.e-com-net.com/image/info8/050e5bdd936e409885d72c8cfd35cb0b.gif)
此时已与两个变数的变异程度、单位和N大小都没有关系，是一个不带单位的纯数，可用来比较不同双变数总体的相关程度和性质。相关系数是两个变数标准化离差的乘积的平均数。
样本相关系数： 
![r\in [-1,1]](http://img.e-com-net.com/image/info8/1920a286410c4fd19447d9566d764fba.gif){kind=small}
上述结果可由回归分析得出：
y 的平方和 
在回归分析中分成两部分：离回归平方和 
和回归平方和 
。后者是由X的不同而引起的。若坐标点愈靠近回归线，则U对
的比率愈大，直线相关就愈密切，又可定义为：
上式说明，当散点图上的点完全落在回归直线上时，Q=0，U=，r=
1;
y变异和x完全无关时，U=0，Q=，r=0;
双变数的相关程度决定于|r|,|r|越接近于1，相关越密切，越接近于0，越可能无关。
r的显著与否与自由度有关，自由度越大，受抽样误差的影响越小，r达到显著水平
的值就越小。
r和b的分母总为正值，分子部分SP，相关系数和回归系数的正负一致。
二、决定系数（determination coefficient）
定义为由x不同而引起的平方和
占总平方和的比率；
也可定义为由y不同而引起的x的平方和
占总平方和
的比率。
决定系数和相关系数的区别：
（1）除掉r=0和|r|=1的情况，
总是小于|r|。可防止对相关系数所表示的相关程度作夸张的解释。
（2）r可正可负，一律取正，取值范围[0,1]。
在相关分析中将两者结合起来是可取的，r的正负表示相关的性质，的大小表示相关程度。
三、相关系数的假设测验
（1）=0的假设测验
测验一个样本相关系数r所来自的总体相关系数 是否为0，统计假设：
:
对 
:
.
由于抽样误差，从的总体中抽得的r并不一定为0.为了判断r代表的总体是否确有直线相关，必须测定实得r值来自总体的概率。只有在这一概率小于0.05时，才能冒5%以下的风险，推断这个样本所属的总体总是有线性相关的。
在的总体中抽样，r的分布随样本容量n的不同而不同。n=2时，r的取值只有-1和1两种，其概率各为0.5；n=3时r的分布呈U型，r=0的概率密度最小，r愈趋向1，概率密度愈大；n=4时分布呈矩形，r在[-1,1]范围内具有相同的概率密度；只有当n
5时分布才逐渐转钟型。由于r的取值区间只有[-1,1]，r本身并不服从某个已知的理论分布。r抽样误差：
对于同一资料来说，线性回归的显著性和线性相关的显著性一定等价，不是偶然巧合而是必然结果。所以在实践应用上，回归的显著性已测验，相关的显著性就无需测验，反之亦然。
r的临界值：
（2）=C的假设测验
测验一个实得的相关系数r与某一指定的或理论的相关系数C是否有显著差异，统计假设为：:
对 :
时，r的抽样分布具有很大的偏态，且随n和的取值而异，将r转换为z：
（3） 
=
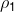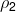的假设测验
测验两个样本相关系数 
和 
分别来自的总体相关系数 和 是否相等，统计假设为：: = 对 : 
由于r转换成z后才近似正态分布，，需进行z转化，两个z值的差数标准误为：
若原假设被接受，应将 和 合并为一个r来表示整个资料的相关情况。
合并的方法是将两样本的平方和和乘积和分别带入
。合并后的r值为：
代表两个样本有共同的相关系数r。