12月16日第二次上（zi）机（bi）考试良心题解

前言

嗯……呃……嘶……算了不知说什么，祝大家身体健康。

Problem A 筛素数

这题这么水，相信大家都AK了

题意：求$[1,n]$内的素数。$N$多大你猜你猜你猜猜想不到吧~反正绝对不是$10^7$!

好了，既然是第二次考质数，那我就简单讲讲欧拉筛的原理吧。
欧拉筛是一种线性筛法，复杂度是$O（n）$的,原理是每个数只会被筛一次。
而且保证了每个数只会被最小的因子筛到，如$12=2\ast 3\ast 3$，由$2$去筛它，$105=3\ast 5\ast 7$，由$3$去筛它。

欧拉筛枫版：

#include
#include
#include
#define fo(i,j,k) for (int i=j;i<=k;i++)
#define N 1000005
using namespace std;
int n,vis[N],dt[N],t;
void pre(int x){
	fo(i,2,x){
		if (!vis[i]) dt[++t]=i;
		fo(j,1,t) if (dt[j]*i>x) break;else{
			vis[i*dt[j]]=1;
			if (i%dt[j]==0) break;  //决定性的break
		}
	}	
}
int main(){
		//freopen("xx.in","r",stdin);
		scanf("%d",&n);
		pre(n);
		fo(i,1,t) printf("%d\n",dt[i]);
		return 0;
}

朴素素数判断冰版

#include 

const int maxn = 1e4 + 5;

int main() {

	int nprime[maxn] = { 1, 1 }, i, j, n;

	for (i = 2; i < maxn; ++i) {

		if (!nprime[i]) { // nprime[i] == 0, 表示是素数

			for (j = i * i; j < maxn; j += i) nprime[j] = 1;
		}
	}
	scanf("%d", &n);
	for (i = 2; i <= n; ++i) {

		if (nprime[i]) continue;
		printf("%d\n", i);
	}
	return 0;
}

Problem B 水仙花数

这题这么水，相信大家都AK了

题意：给定一个三位数，判断是否为水仙花数，水仙花数定义：当且仅当各个位数的立方和等于本身的数。

暴力分解个位十位百位的立方求和判断。
有的同学喜欢用$pow()$函数也可以，不过需要注意$pow()$函数的参数和返回值都是$double$哦！

枫版

#include
#include
#include
#define fo(i,j,k) for (int i=j;i<=k;i++)
using namespace std;
int n;
int pan(int x){
		int a,b,c;
		a=x/100;
		b=x/10%10;
		c=x%10;
		if (a*a*a+b*b*b+c*c*c==x) return 1;
		return 0;
}
int main(){
		//freopen("xx.in","r",stdin);
		scanf("%d",&n);
		int x;
		fo(i,1,n){
			scanf("%d",&x);
			if (pan(x)) printf("YES\n");else printf("NO\n");
		}
		return 0;
}

冰版

#include 

int conv(int num) {

	int k, sum = 0;
	while (num > 0) { // 逐位分离

		k = num % 10;
		sum += k * k * k;
		num /= 10;
	}
	return sum;
}

int main() {

	int t, num;

	scanf("%d", &t);
	while (t--) {

		scanf("%d", &num);
		printf("%s\n", conv(num) == num ? "YES" : "NO");
		// cout << (conv(num) == num ? "YES" : "NO") << endl;
	}
	return 0;
}

problem C 回文字符串

这题这么水，相信大家都AK了

题意：求字符串的最大回文子串，长度相同的位置靠左优先。

暴力解:

需要分两种情况：
$$1、中心点在字符本身（言下之意长度是奇数）$$
$$2、中心点在字符之间（言下之意长度是偶数）$$
或者$dalaoiceup$的添加’#'字符法也可行！
然后从中心点往左右延伸就行了，复杂度$O(T{n}^2)$

但是由于出题人太过于良心，暴力不仅能过竟然还是$0ms$！一时语塞$.jpg$
为啥过不了，自己可以构造一个长度$10000$全是一样字符的字符串，跑跑就知道了。

正解：$Manacher$马拉车算法，复杂度$O(Tn)$

首先，要做个预处理，在字符串头加’$’,字符之间加’#’，避免了讨论。
如"aabb"可以变成"$#a#b#b#a#",而在开头加美元的目的，是为了让"偶数"和"奇数"型回文串的信息一致化。
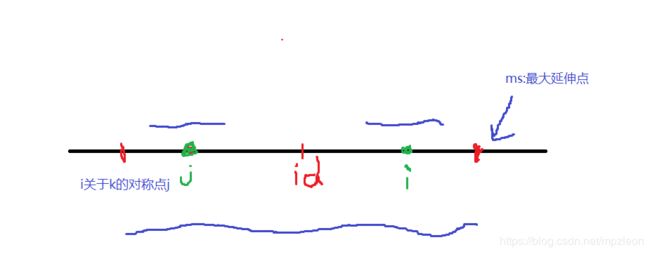
简单地来说，就是利用了一个对称点（k），复制了当前点(i)关于点(k)的对称点(j)的信息。
我们不妨设
$$p[i]:以i为中心位置的最大回文子串半径$$
$$ms:当前最大的延伸点，即max(p[k]+k)$$
$$id:最大延伸回文串的中心点$$
如下图所示，画的丑别在意 ，蓝色线表示虚拟的回文串，所以就有下面的递推式。
但是这样还不够，如果正好$p[i]$取了$ms-i$的值，则需要继续左右延伸，并更新答案，$ms$等。
$$if(ms>i)p[i]=min(p[2\ast id-i],ms-i);elsep[i]=1;$$
其中，由规律可得，起点为$\frac{i-p[i]}{2}$,真实长度为$p[i]-1$。

$Manacher$枫版

#include
#include
#include
#include
#include
#include
#define fo(i,j,k) for (int i=j;i<=k;i++)
#define N 100005
using namespace std;
int p[N],n;
string s;
void solve(string s){
		string x="$#";
		int ans=0,len=0,ms=0,id=0;
		for (int i=0;i<s.size();i++) x=x+s[i]+"#";
		for (int i=0;i<x.size();i++){
			if (ms>i) p[i]=min(p[2*id-i],ms-i);else p[i]=1;
			while (x[i+p[i]]==x[i-p[i]]) p[i]++;
			if (ms<i+p[i]){
				ms=i+p[i];
				id=i;
			}
			if (len<p[i]){
					len=p[i];
					ans=i;
			}
		}
		cout<<s.substr((ans-len)/2,len-1)<<endl;
}
int main(){
	//freopen("xx.in","r",stdin);
	cin>>n;
	for (int i=1;i<=n;i++){
			cin>>s;
			solve(s);
	}
	return 0;
}

奇丑的暴力$char$枫版

#include
#include
#include
#define fo(i,j,k) for (int i=j;i<=k;i++)
#define N 100005
using namespace std;
int n,st,ans;
char c[N];
void up(int x,int y){                    //用来更新答案的
		if ((x>ans)||((x==ans)&&(y<st))){
				st=y;
				ans=x;
		}
}
int main(){
	//	freopen("xx.in","r",stdin);
		scanf("%d",&n);
		int x,l,k;
		fo(i,1,n){
				ans=0;st=0;
				scanf("%s",c+1);
				l=strlen(c+1);
				fo(j,1,l){							//ans是最大长度，st是起点位置，k是半径
					k=1;
					while ((j-k>=1)&&(j+k<=l)&&(c[j-k]==c[j+k])) k++;	//奇数长度
					up(k*2-1,j-k+1);
					k=0;
					while ((j-k>=1)&&(j+k+1<=l)&&(c[j-k]==c[j+k+1])) k++;//偶数长度
					up(k*2,j-k+1);
				}
			fo(i,st,ans+st-1) printf("%c",c[i]);
			printf("\n");
		}		
		return 0;
}

暴力冰版

#include 
#include 

const int maxn = 1e4 + 5;

char s1[maxn], s2[maxn * 2];
int n1, n2;

int find(int pos, int &ans) {

	int i, j;
	if (s2[pos] != '#') ++ans;
	for (i = pos - 1, j = pos + 1; i >= 0 && j < n2; --i, ++j) {

		if (s2[i] != s2[j]) return i + 1;
		if (s2[i] != '#') ans += 2;
	}
	return i + 1;
}

int main() {

	int t, i, j, tpos, tans, pos, ans;

	scanf("%d", &t);
	while (t--) {

		pos = 0, ans = 1;
		scanf("%s", s1);
		n1 = strlen(s1);
		n2 = n1 * 2 + 1;
		for (i = j = 0; i < n2; ++i) {

			if (i & 1) s2[i] = s1[j++];
			else s2[i] = '#';
		} // 插入'#', 字符串长度为奇数, 避免分类讨论
		s2[n2] = '\0';

		for (i = 1; i < n2 - 1; ++i) { // 枚举回文串中点, 左右两边逐位比较

			tans = 0;
			tpos = find(i, tans);
			if (tans > ans) pos = tpos, ans = tans;
		}
		for (i = pos; ans; ++i) {

			if (s2[i] == '#') continue;
			--ans; printf("%c", s2[i]);
		}
		printf("\n");
	}
	return 0;
}

Problem D 字符串比较

这题这么水，相信大家都AK了

题意：给定三个字符串，按字典序单调不下降排列。

丑到没朋友，丑到单身，丑到自闭，丑到想死，丑到不能再丑的的考试枫版

#include
#include
#include
#include
#define fo(i,j,k) for (int i=j;i<=k;i++)
#define N 100005
using namespace std;
int n,st,ans;
char c1[N],c2[N],c3[N];
void s(char (&a)[N],char (&b)[N]){
		char t[N];
		strcpy(t,a);
		strcpy(a,b);
		strcpy(b,t);
}
int main(){
	//	freopen("xx.in","r",stdin);
		scanf("%s%s%s",c1,c2,c3);
		if (strcmp(c1,c2)>0) s(c1,c2);
		if (strcmp(c1,c3)>0) s(c1,c3);
		if (strcmp(c2,c3)>0) s(c2,c3);
		cout<<c1<<endl<<c2<<endl<<c3;
		return 0;
}

重新做人指针交换枫版

#include
#include
#include
#include
#define fo(i,j,k) for (int i=j;i<=k;i++)
#define N 100005
using namespace std;
int n,st,ans;
char c1[N],c2[N],c3[N];
int main(){
		freopen("xx.in","r",stdin);
		scanf("%s%s%s",c1,c2,c3);
		char *a,*b,*c;
		a=c1;b=c2;c=c3;
		if (strcmp(a,b)>0) swap(a,b);
		if (strcmp(a,c)>0) swap(a,c);
		if (strcmp(b,c)>0) swap(b,c);
		cout<<a<<endl<<b<<endl<<c;
		return 0;
}

冰版

#include 
#include 
#include 

using namespace std;

int main() {

	string str[3];
	for (int i = 0; i < 3; ++i) cin >> str[i];
	sort(str, str + 3);
	for (int i = 0; i < 3; ++i) cout << str[i] << endl;
	return 0;
}

Problem E 最小公倍数

这题这么水，相信大家都AK了

题意：求两个数最小公倍数

敲黑板！$lcm(a,b)=\frac{a\ast b}{gcd(a,b)}$记几试着整理整理，证明一下，要记住的。
$gcd$用辗转相除法求即可。
枫版

#include
#include
#include
#include
#include
#define fo(i,j,k) for (int i=j;i<=k;i++)
#define N 100005
using namespace std;
int n,st,ans,a,b,c;
int main(){
		//freopen("xx.in","r",stdin);
		scanf("%d%d",&a,&b);
		c=__gcd(a,b);                              //偷了个小懒，用内置gcd
		printf("Least common multiple: %d",a*b/c);
		return 0;
}

冰版

#include 

int gcd(int a, int b) { // 辗转相除法

	return b ? gcd(b, a % b) : a;
}

int lcm(int a, int b) {

	return a / gcd(a, b) * b;
}

int main() {

	int a, b;

	scanf("%d%d", &a, &b);
	printf("Least common multiple: %d", lcm(a, b));
	return 0;
}

Problem F 奖学金测评

这题这么水，相信大家都AK了

题意 现在已经得到了每位同学的姓名，德育分，智育分和文体分，想请你继续完成这个程序，利用这些数据得出每位同学的最终分数和全班的排名。 每位同学的最终分数为各项的加权得分之和，加权得分即为该项得分乘以相应的权值。德育的权值为30%×3，智育的权值为40%×3，文体的权值为30%×3，（结果保留了一位小数）。

没办法，用$struct$吧，快捷好省,另外$dalaoiceup$附加了$cin$和$cout$的输出注释。
枫版

#include
#include
#include
#include
#include
#define fo(i,j,k) for (int i=j;i<=k;i++)
#define N 10005
using namespace std;
int n,st,ans;
struct ee{
		double a;
		double b;
		double c;
		double d;
		char s[100];
}q[N];
bool cmp (ee a,ee b){
		return a.d>b.d;
}
int main(){
		//freopen("xx.in","r",stdin);
		//freopen("x1.out","w",stdout);
		scanf("%d",&n);
		fo(i,1,n){
				scanf("%s%lf%lf%lf",q[i].s,&q[i].a,&q[i].b,&q[i].c);
				q[i].d=q[i].a*0.9+q[i].b*1.2+q[i].c*0.9;
		}
		sort(q+1,q+1+n,cmp);
		printf("rank     name         score\n");
		fo(i,1,n){
				printf("%d %10s %14.1lf\n",i,q[i].s,q[i].d);
		}
		return 0;
}

$dalaoiceup$版

#include
#include
//#include
//#include 

using namespace std;
const int maxn = 1e4 + 5;

struct Stu {
	char name[100];
	double score;
	bool operator < (const Stu &a) const { return score > a.score; }
} stu[maxn];

int main() {

	int n, i;
	double a, b, c;
	
	scanf("%d", &n);
	for (i = 0; i < n; ++i) {

		scanf("%s%lf%lf%lf", stu[i].name, &a, &b, &c);
		stu[i].score = a * 0.3 * 3 + b * 0.4 * 3 + c * 0.3 * 3;
	}
	sort(stu, stu + n);

	printf("rank     name         score\n");
	for (i = 0; i < n; ++i) {

		printf("%-4d%8s%15.1lf\n", i + 1, stu[i].name, stu[i].score);
		// cout << left << setw(4) << i + 1 << right << setw(8) << stu[i].name 
		// << setw(15) << fixed << setprecision(1) << stu[i].score << endl;
	}
	return 0;
}

Problem G 子网掩码

这题这么水，相信大家都AK了

题意 大概是给定一个本地IP地址，一个子网掩码，N个其它IP地址，问有多少个IP跟本地在一个子网络上，两台计算机各自的IP地址与子网掩码进行AND运算后，如果得出的结果是相同的，则说明这两台计算机是处于同一个子网络上的。

首先，IP地址和子网掩码都是xxx.xxx.xxx.xxx的形式，所以我们分别求出来直接判断就好了。

冰版

#include 

int read() {

	int ret, a, b, c, d;
	scanf("%d.%d.%d.%d", &a, &b, &c, &d);
	ret = d + (c << 8) + (b << 16) + (a << 24); // 位移运算
	return ret;
}

int main() {

	int i, n, mask, aim, num;

	aim = read();
	mask = read();
	aim &= mask;

	scanf("%d", &n);
	while (n--) {

		num = read(); // & 位与
		printf("%s\n", (num & mask) == aim ? "INNER" : "OUTER");
	}
	return 0;
}

字符串法枫版

#include
#include
#include
#include
#include
#define fo(i,j,k) for (int i=j;i<=k;i++)
#define N 10005
using namespace std;
int n,st,ans,b[4],c[4];
char s[N],s1[N],s2[N];
void chang(int (&a)[4],char s1[N],char s2[N]){
		int p1,p2,x1=1,x2=1;
		fo(i,0,3){
			p1=0;
			p2=0;
			while (s1[x1]!='.'&&s1[x1]!='\0') {
					p1=p1*10+s1[x1]-'0';
					x1++;
			}
			while (s2[x2]!='.'&&s2[x2]!='\0') {
					p2=p2*10+s2[x2]-'0';
					x2++;
			}
			a[i]=p1&p2;
			x1++;x2++;
		}
}
int main(){
		//freopen("xx.in","r",stdin);
		scanf("%s%s%d",s1+1,s2+1,&n);
		chang(b,s1,s2);
		int p;
		fo(i,1,n){
				scanf("%s",s+1);
				chang(c,s,s2);
				p=1;
				fo(i,0,3) if (b[i]!=c[i]){
						p=0;
						break;
				}
				if (p) printf("INNER\n");else printf("OUTER\n");
		}
		return 0;
}

后语

祝大家编程快乐！