Unity求一条直线与平面的交点

这个是面试官经常考的一个问题，我们先把它变成一个数学问题。

已知一个平面上的一点P0和法向量n，一条直线上的点L0和方向L,求该直线与该平面的交点P

如下图

首先我们分析一下我们知道平面和直线的法向量，知道平面和直线上的一点，求直线与平面上的交点p。

这里我们就要引入点积的概念。点积的几何意义(百度百科直接粘的)

设二维空间内有两个向量

   

和

   

，它们的夹角为

   

，则内积定义为以下实数：  [2]  

该定义只对二维和三维空间有效。

这个运算可以简单地理解为：在点积运算中，第一个向量 投影到第二个向量上（这里，向量的顺序是不重要的，点积运算是可交换的），然后通过除以它们的标量长度来“标准化”。这样，这个分数一定是小于等于1的，可以简单地转化成一个角度值。

简单点来说当我们使用Vector3.Dot来处理两个标准化的向量的时候会得到两个向量角度的COS值。

也就是说如果两个向量垂直的话，cos值为0，也就是说两个向量垂直的话点积为0.

      而p和po组成的直线肯定与平面法向量n垂直。

      这里我们就能推倒出已知的公式1：(p-p0)*n=0

      而由于交点p是属于直线上的一点，所以我们能推倒出公式2:P=L0+dL;

     然后我们把公式2导入到公式1得到：

      (L0+dL-P0)*n=0

      (L0-P0)*n+dL*n=0(点乘满足分配率)

      (p0-L0)*n=dL*n

       d=(p0-L0)*n/L*n(点乘满足结合律)

     只要我们求出d的值带入公式2就能求出交点P.

*************************************************************************************************    

最后又引申出一个问题，如果这个平面是有边界的，那么我们就还得求一下这个平面是否与直线相交。

这里我用了个简单方法。首先你必须知道这个平面所有的顶点，然后这个多边形必须是凸多边形。

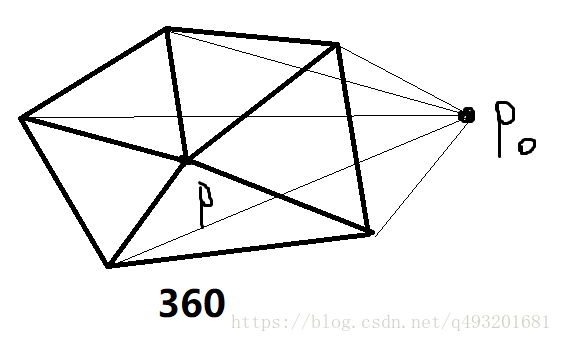
那么它必定满足如下规律，如图

      如果该点位于平面内，那么由改点到顶点组成的向量之间的夹角之和必定等于360度，

      如果位于平面外，那么由改点到顶点组成的向量之间的夹角之和必定小于360度，

      所以我们只要求出夹角之和就能求出改点是否位于平面内。

     当然这个只适用于凸多边形，如果有更好地办法，欢迎评论讨论。

********************************************************************************************

    我在Unity中自己创建了一个三角面mesh，然后自己设置一条直线。求交点P，然后赋予小球这个位置。

   在三角面内为红色，在三角面外围蓝色。以下是实现截图。

   

     

实现代码

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class S001 : MonoBehaviour
{
    public Material mat;//三角形材质
    private Mesh mesh;//三角形mesh
    private GameObject GoSphere;//交点
    private Vector3 vecLinePoint;//直线的方向

    //面需要的点
    private List vertices = new List();
    //生成三边面时用到的vertices和index
    private List triangles = new List();
    //直线
    public List veclines;
    void OnDrawGizmos()
    {
        if (veclines.Count > 1)
        {
            Gizmos.DrawLine(veclines[0], veclines[1]);
        }
      
    }

    private void Awake()
    {
        this.gameObject.AddComponent();
        this.gameObject.AddComponent();
        mesh = new Mesh();
        AddFrontFace();
        //为点和index赋值
        mesh.vertices = vertices.ToArray();
        mesh.triangles = triangles.ToArray();
        //重新计算顶点和法线
        mesh.RecalculateBounds();
        mesh.RecalculateNormals();
        //将生成的面赋值给组件
        GetComponent().mesh = mesh;
        GetComponent().material = mat;
        print(mesh.normals[0]);
        //直线的两个点
        veclines.Add(new Vector3(0,1,-10));
        veclines.Add(new Vector3(0.11f,0.36f,3));
        GoSphere = GameObject.CreatePrimitive(PrimitiveType.Sphere);
        GoSphere.transform.localScale = new Vector3(0.05f, 0.05f, 0.05f);
    }
    float i = 0;
    void Update()
    {
        if (i > 2)
        {
            vecLinePoint = (veclines[1] - veclines[0]);//计算直线的方向
            Vector3 vec = GetIntersectWithLineAndPlane(veclines[0], vecLinePoint, mesh.normals[0], mesh.vertices[0]);
            //print(vec.x+"*******"+vec.y+"*********"+vec.z);
            GoSphere.transform.position = vec;//赋值
            bool k = IsVecPosPlane(mesh.vertices, vec);//交点是否在多边形内部
            if (k)//如果在范围内是红色，在范围外是蓝色
            {
                GoSphere.GetComponent().material.color = Color.red;
            }
            else
            {
                GoSphere.GetComponent().material.color = Color.blue;
            }

            print(k);
            //计算位置
            i = 0;
        }
        else
        {
            i += Time.deltaTime;
        }
    }
    /// 

    /// 计算直线与平面的交点
    /// 
    /// 直线上某一点
    /// 直线的方向
    /// 垂直于平面的的向量
    /// 平面上的任意一点
    /// 
    private Vector3 GetIntersectWithLineAndPlane(Vector3 point, Vector3 direct, Vector3 planeNormal, Vector3 planePoint)
    {
        float d = Vector3.Dot(planePoint - point, planeNormal) / Vector3.Dot(direct.normalized, planeNormal);
        //print(d);
        return d * direct.normalized + point;
    }
    /// 

    /// 确定坐标是否在平面内
    /// 
    /// 
    private bool IsVecPosPlane(Vector3[] vecs, Vector3 pos)
    {
        float RadianValue = 0;
        Vector3 vecOld = Vector3.zero;
        Vector3 vecNew = Vector3.zero;
        for (int i = 0; i < vecs.Length; i++)
        {
            if (i == 0)
            {
                vecOld = vecs[i] - pos;
            }
            if (i == vecs.Length - 1)
            {
                vecNew = vecs[0] - pos;
            }
            else
            {
                vecNew = vecs[i + 1] - pos;
            }
            RadianValue += Mathf.Acos(Vector3.Dot(vecOld.normalized, vecNew.normalized)) * Mathf.Rad2Deg;
            vecOld = vecNew;
        }
        if (Mathf.Abs(RadianValue - 360) < 0.1f)
        {
            return true;
        }
        else
        {
            return false;
        }
        //vecOld = vecs[0] - pos;
        //vecNew = vecs[1] - pos;
        //RadianValue += Mathf.Acos(Vector3.Dot(vecOld.normalized, vecNew.normalized)) * Mathf.Rad2Deg;
        ////
        //vecOld = vecs[1] - pos;
        //vecNew = vecs[2] - pos;
        //RadianValue += Mathf.Acos(Vector3.Dot(vecOld.normalized, vecNew.normalized)) * Mathf.Rad2Deg;
        ////
        //vecOld = vecs[2] - pos;
        //vecNew = vecs[0] - pos;
        //RadianValue += Mathf.Acos(Vector3.Dot(vecOld.normalized, vecNew.normalized)) * Mathf.Rad2Deg;
    }
    void AddFrontFace()
    {
        //添加4个点
        vertices.Add(new Vector3(0, 0, 0));
        vertices.Add(new Vector3(0, 1, 0));
        vertices.Add(new Vector3(1, 0, 0));
        triangles.Add(0);
        triangles.Add(1);
        triangles.Add(2);
    }
}