C数据结构和使用详情（基础）

写在前面

本篇继上篇文章重点介绍数据结构的使用方法，主要针对不同的数据结构的创建、增删改查等基础操作，又根据每个数据结构的特点延伸出特色的其他使用方向。

0、数组

面试中常见问题：
1、寻找数组中第二小的元素
【解答】利用排序算法，先排序再遍歷找

2、找到数组中第一个不重复出现的整数参考文献
【解答】这种对查找顺序有要求的，不能先排序，双循环查找（On²）

hash表，（bitmap形式），循环一次，将所有的不重复的数找到，然后按照找第一个出现的数

3、找到數組中的第一個重複出現的整數
【解答】用hash表較好，记录每一个出现出的索引，第二查找到发现对应的hash值大于零，则读取索引即为第一个重复数的

4、合并两个有序数组
【解答】双指针比較

5、重新排列数组中的正值和负值
【推荐解答】構建兩個堆空間，遍歷一次將正數和負數分別存入，再合併，需要空間較大

• 負數在前，正數在後；begin爲正數，end爲負數，交換位置
• 負數在後，正數在前；begin爲負數，end爲正數，交換位置

1、堆、栈

堆
堆是一种经过排序的树形数据结构，每个结点都有一个值，类似于倒过来的树结构。
通常我们所说的堆的数据结构，是指二叉堆。堆的特点是根结点的值最小（或最大），且根结点的两个子树也是一个堆。由于堆的这个特性，常用来实现优先队列，堆的存取是随意。（堆中某个结点的值总是不大于或不小于其父结点的值，堆总是一棵完全二叉树）
栈
栈就像装数据的桶或箱子，是一种具有后进先出（FILO）性质的数据结构，也就是说后存放的先取，先存放的后取。
【数据结构的堆和栈和程序结构中所说的堆栈的区别】

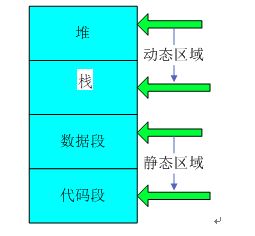
1、栈区(stack):由编译器自动分配释放，存放函数的参数值，局部变量等值。其操作方式类似于数据结构中的栈
2、堆区(heap):一般由程序员分配释放，若程序员不释放，则可能会引起内存泄漏。注堆和数据结构中的堆栈不一样，其分配方法类是与链表。程序结束时可能由OS回收
3、程序代码区：存放函数体的二进制代码。
4、数据段：由三部分组成：
1>只读数据段：
只读数据段是程序使用的一些不会被更改的数据，使用这些数据的方式类似查表式的操作，由于这些变量不需要更改，因此只需要放置在只读存储器中即可。一般是const修饰的变量以及程序中使用的文字常量一般会存放在只读数据段中。
2>已初始化的读写数据段：
已初始化数据是在程序中声明，并且具有初值的变量，这些变量需要占用存储器的空间，在程序执行时它们需要位于可读写的内存区域，并且有初值，以供程序运行时读写。在程序中一般为已经初始化的全局变量，已经初始化的静态局部变量(static修饰的已经初始化的变量)
3>未初始化段（BSS）：
未初始化数据是在程序中声明，但是没有初始化的变量，这些变量在程序运行之前不需要占用存储器的空间。与读写数据段类似，它也属于静态数据区。但是该段中数据没有经过初始化。未初始化数据段只有在运行的初始化阶段才会产生，因此它的大小不会影响目标文件的大小。在程序中一般是没有初始化的全局变量和没有初始化的静态局部变量。

2、队列

定义
队列是一种先进先出的线性表，队尾只允许入队（新增），队首只允许出队（删除），简称FIFO。入队将一个数据放到队列尾部；出队从队列的头部取出一个元素。队列的应用也非常广泛如：循环队列、阻塞队列、并发队列、优先级队列等。

队列的基本操作
EnQueue()——在队列尾部插入元素
DeQueue()——移除队列头部的元素
IsEmpty()——如果队列为空，则返回true
Top()——返回队列的第一个元素
【队列操作的代码解释】：

1. 入队的操作是先存入数据、然后将尾指针rear加1，所以尾指针始终指向的是当前的下一个空白区域（未存入数据的地址）
2. 出队操作是将当前头指针front的值清空，然后将头指针加1
3. 队列空的情况——rear == front
4. 队列满的情况——(rear + 1) % maxsize == front
5. 队列存数的数量——((rear - front) + maxsize) % maxsize；其中当rear在front的后面时，两者之差即为存入的数据量，当rear在front的前面时，两者之差为负数，加上maxsize即为数据量

面试中关于队列的常见问题
使用队列表示栈、使用栈来表示队列
解析：队列表示栈，需要两个队列，一个作为主队，压入数据等，取出栈顶数据等，在出栈操作中，辅助队列会存入除主队最后一个元素的其他元素，并将最后一个元素弹出，实现LIFO。
栈表示队列，需要同样的两个栈，压栈就是队列的入队操作，此时第一个元素在栈底，因此出栈时需要将除栈底的其他元素压入辅助栈，并在主栈弹出元素后，将所有的其他的元素压回进主栈，实现FIFO。
对队列的前k个元素倒序、倒置队列
解析：

反向排列	倒置队列，就是全部的元素倒序，用递归方法；首尾设置标志从两边往里，互相替换，分为奇偶两种情况
倒序排列，顺序和排列	每次遍历队列，从中找出最小的元素，放入临时队列，遍历的过程是出队的过程，注意如果一个元素比当前的最小值大，则要放回队列当中，如果比当前的最小值小，则保存起来，暂时不放回队列中，发现更小的，把原来的最小值放入，更新最小值，在遍历完一次以后，将最小值存入临时队列。然后开始第二次遍历，注意每次遍历原队列中都会减少一个元素，因此共遍历队列N次，每次对队列N、N-1、N-2 … 1这么多次出队操作来找最小值，在最后一次完成后临时队列中存放的就是排序好的结果，出队N次即可按非降序输出。

使用队列生成从1到n的二进制数
解析：十进制数化二进制数，整数部分用“除二取余“法，将数除以2，将余数放入栈，商再除以2，重复。直至商为0。小数部分用“乘二取整”法，数乘2，然后取整、放入队列里。

3、链表

链表包括以下类型：
单链表（单向）
双向链表（双向）
双向链表也叫双链表，是链表的一种，它的每个数据结点中都有两个指针，分别指向直接后继和直接前驱。所以，从双向链表中的任意一个结点开始，都可以很方便地访问它的前驱结点和后继结点，一般我们都构造双向循环链表
循环链表是链表的尾节点指向了前驱中的一个节点，一般指向头节点
链表的基本操作：
InsertAtEnd - 在链表的末尾插入指定元素
InsertAtHead - 在链接列表的开头/头部插入指定元素
Delete - 从链接列表中删除指定元素
DeleteAtHead - 删除链接列表的第一个元素
Search - 从链表中返回指定元素
IsEmpty - 如果链表为空，则返回true

进阶用法
推荐博文
https://blog.csdn.net/qq9116136/article/details/80056633?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
0、反向输出一个链表，反向遍历，输出显示
1、删除一个无头单链表的非尾节点（不能遍历链表）
假设删除的是pos节点，我们可以将pos的下一个节点的数据存入pos节点，在删除pos节点的下一个节点即可—将当前的节点的下一个节点的内容存入，有两份相同的节点内容，可删除下一个，而非当前的，找不到其前一个节点
2、在无头单链表的一个节点前插入一个节点（不能遍历链表）
假设在pos前插入一个节点，我们可以先在pos后插入一个与pos数据一样的节点，在将pos的数据改为需要插入的节点值
3、查找单链表的中间节点，（只能遍历一次链表）
给两个指针，第一个指针走一步时第二个指针走两步，当快指针走完时慢指针走到中间节点。
查找单链表的倒数第K节点，（只能遍历一次链表）
同样定义两个指针，快指针先走k步，慢指针开始走，当快指针走完时慢指针走到倒数第K个节点。
4、构造一个带环链表
找到环入口的节点，让尾节点指向入口节点。
5、求链表中环的长度
定义两个快慢指针，快指针走两步慢指针走一步，即快指针速度是慢指针的2倍，当他们在环里第一次相遇时结束，再让他们继续走，第二次相遇时快指针一定比慢指针快了环的长度步。

面试中关于链表的常见问题
反转链表
递归法和迭代法，其中迭代法选取三个指针指向链表的1、2、3节点，交换1、2的next内容，互换方向；更新1为2、2为3、3---->4，最后判断2的指向是否为空。
检测链表中的循环
设定两个指针p1、p2，每次循环p1向前走一步，p2向前走两步。直到p2碰到NULL指针或者两个指针相等结束循环，如果两个指针相等则说明存在环。
返回链表倒数第N个节点
方法以上已解答
删除链表中的重复项
思路一：
遍历链表，把遍历的值存储到一个Hashtable中，在遍历过程中，若当前访问的值在Hashtable中已经存在，则说明这个数据是重复的，因此就可以删除。
优点：时间复杂度较低O(n)
缺点：在遍历过程中需要额外的存储空间来保存已遍历过的值
思路二：
对链表进行双重循环遍历，外循环正常遍历链表，假设外循环当前遍历的结点为cur，内循环从cur开始遍历，若碰到与cur所指向结点值相同，则删除这个重复结点
优点：不需要额外的存储空间
缺点：时间复杂度较高O(n^2)
约瑟夫环问题
循环链表的使用，数组迭代，递归方式

先不断迭代找到尾节点，让尾节点的next指针指向头节点，这样形成了一个环，
接着进入循环，循环的结束条件为只剩一个节点。不断地迭代k次然后删除当前节点。
		SListNode* str, *tail;
		int i = 0;
		str = pHead;
		tail = pHead;
		while (tail->next)
		{
			tail = tail->next;
		}
		tail->next = pHead;
		while (str->next!=str)
		{
			for (;i < k;++i)
			{
				str = str->next;
			}
			str->data = str->next->data;
			str->next = str->next->next;
			free(str->next);
		}
		return str;

4、二叉树

常见概念与性质
结点：表示树中的元素
结点的度：结点含有的子树数
叶子：度为0的结点
层次：从根结点算起，根为第一层
深度：树中结点最大的层次数
1、二叉树的第i层至多有2^(i-1)个结点
2、深度为k的二叉树至多有2^k-1个结点
3、对于任何一棵二叉树T，如果终端结点数为n0，度为2的结点数为n2，则n0 = n2 + 1
定义
二叉树是每个节点最多有两棵子树的树结构。通常子树被称作“左子树”和“右子树”，每个节点最多有两个子树，即没有度大于2的节点，且左右顺序不能颠倒，二叉树常被用于实现二叉查找树和二叉堆，链接：https://www.jianshu.com/p/230e6fde9c75
满二叉树
一棵深度为k，且有2^k-1个节点的二叉树称之为满二叉树，除了叶子结点，所有结点的度为2
完全二叉树
深度为k，有n个节点的二叉树，当且仅当其每一个节点都与深度为k的满二叉树中，序号为1至n的节点对应时
①叶子结点只可能出现在层次最大的两层上
②任意一个结点，其右分支下子孙的最大层次为I，则其左分支下子孙的最大层次数必为I或者I+1
二叉排序树、二叉查找树、BST
二叉查找树就是二叉排序树，也叫二叉搜索树。二叉查找树或者是一棵空树，或者是具有下列性质的二叉树
(1) 若左子树不空，则左子树上所有结点的值均小于它的根结点的值
(2) 若右子树不空，则右子树上所有结点的值均大于它的根结点的值
(3) 左、右子树也分别为二叉排序树；(4) 没有键值相等的结点
平衡二叉树
平衡二叉树又称AVL树，它或者是一棵空树，或者是具有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1
AVL树是最先发明的自平衡二叉查找树算法。在AVL中任何节点的两个儿子子树的高度最大差别为1，所以它也被称为高度平衡树，n个结点的AVL树最大深度约1.44log2n。查找、插入和删除在平均和最坏情况下都是O（log n）。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树
红黑树
红黑树是平衡二叉树的一种，它保证在最坏情况下基本动态集合操作的事件复杂度为O(log n)，红黑树和平衡二叉树区别如下：(1) 红黑树放弃了追求完全平衡，追求大致平衡，在与平衡二叉树的时间复杂度相差不大的情况下，保证每次插入最多只需要三次旋转就能达到平衡，实现起来也更为简单。(2) 平衡二叉树追求绝对平衡，条件比较苛刻，实现起来比较麻烦，每次插入新节点之后需要旋转的次数不能预知
哈夫曼樹
给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。
哈夫曼树和编码详细
基本操作
构造二叉树的方法：
1、顺序存储结构，按照层次结点依次编号，无结点的地方用0替代，浪费空间、适于满二叉树和完全二叉树
2、链式存储结构，data\ lchild\ rchild
3、三叉链表，data\ lchild\ rchild\ parent
遍历的方法：

先序排列	若二叉树为空，则空操作，否则先访问根节点，再先序遍历左子树，最后先序遍历右子树
中序排列	二叉树为空，则空操作，否则先中序遍历左子树，再访问根节点，最后中序遍历右子树
后序排列	若二叉树为空，则空操作，否则先后序遍历左子树，再后序遍历右子树，最后访问根节点
层次排列	若二叉树为空，则空操作，否则按照层次结构依次从根结点开始访问

增删改查的方法：
删除结点有三个情况

1.被删除的结点是叶子结点	直接删除即可
2.被删除的结点有一个叶子结点（左右相同）	将其唯一子节点与父结点相连，原来是父结点的左结点，那么其儿子节点仍连为父结点的左结点
3.被删除的结点有两个叶子结点	右子结点代替被删除结点，继承它的位置，原来的左儿子继续当右儿子的左结点

面试中关于树结构的常见问题

1、距离根节点距离K的节点 | 距离任意节点距离为K的节点
2、查找BST中任意2节点的LCA | 查找任意二叉树中任意2节点的LCA
3、查找给定节点的祖先节点

求二叉树的高度
【解答】遞歸左右子樹，選擇其中數值大的，即爲樹的高度
在二叉搜索树中查找第k个最大值
【解答】BST的中序排列時，正好是按照升序的方式，從右往左遍歷即可找到第k個最大值
查找与根节点距离k的节点
【解答】递归查询，直到k次後打印結點內容

• 若是任意一點的距离为k的結點，按照向父節點和子孫結點兩個方向搜索，若是距離超過了根節點，則需要按照距離根節點距離x，向根的右結點搜索k-x處結點即可

查找兩個結點的最近公共祖先LCA
【參考解答】
在二叉树中查找给定节点的祖先节点
【解答】1、顺序存储（完全二叉树），假设根的存储下标是1
将当前结点的下标连续整除以2，直到1为止，中间所有得到的商的下标都是其祖先，并且是从回其双亲直到根为止
2、链式存储
使用非递归的后序遍历，当遍历到该结点时，辅助栈中从栈顶到达栈底依次为该结点从双亲开始到根为止的所有祖先

非递归的后序遍历二叉树
do{
while(p != NULL)
{
	st[top++] = p;
	p = p->left;
}
tp = NULL;
flag = 1;
while(top && flag)
{
	p = st[--top];
	if(p->right == tp)
	{
		printf
	}
	else
	{
		p = p->right;
		flag = 0;
	}
}
}
while(top);

【树类型题目框架】
明確一個節點需要做的事情，剩下的事情交給框架

void tree(TreeNode root)
{
	//root 需要做什麼？
	tree(root.left);
	tree(root.right);
}

5、哈希表

简单定义
hash函数就是根据key计算出该存储地址的位置，hash表就是基于hash函数建立的一种查找表。
哈希算法、散列算法
就是把任意长度的输入（又叫做预映射， pre-image），通过散列算法，变换成固定长度的输出，该输出就是散列值。这种转换是一种压缩映射，也就是，散列值的空间通常远小于输入的空间，不同的输入可能会散列成相同的输出，而不可能从散列值来唯一的确定输入值
哈希表
哈希表是根据设定的哈希函数H（key）和处理冲突方法将一组关键字映射到一个有限的地址区间上，并以关键字在地址区间中的象作为记录在表中的存储位置，这种表称为哈希表或散列，所得存储位置称为哈希地址或散列地址。作为线性数据结构与表格和队列等相比，哈希表无疑是查找速度比较快的一种。

key	我们输入待查找的值
hash函数（散列函数）	存在一种函数F，根据这个函数和查找关键字key，可以直接确定查找值所在位置，而不需要一个个遍历比较。这样就预先知道key在的位置，直接找到数据，提升效率。即地址index=F(key)
hash值	key通过hash函数算出的值（对数组长度取模，便可得到数组下标）
value	我们想要获取的内容

运算过程
F(key) = hash
hash % p–(mod m) = index
（该过程需要解决index冲突问题）
Q(index) = value

哈希函数设计考虑因素

计算hash地址的时间	表长
关键字的长度	关键字是否分布均匀
尽量减少冲突

设计方法
推荐博文
直接定址法、数字分析法、平方取中法、折叠法、随机数法、除留余数法

解决hash冲突
推荐博文
对不同的关键字可能得到同一散列地址，即k1≠k2，而f(k1)=f(k2)，或f(k1) MOD 容量 =f(k2) MOD 容量，这种现象称为碰撞，亦称冲突
开放定址法（线性探测再散列、二次探测再散列、伪随机数散列法）
链地址法
再哈希法（建立两个不同规则的哈希函数）
建立公共溢出区
其中，线性探测再散列比较常用

面试中关于哈希结构的常见问题：
在数组中查找对称键值对
追踪遍历的完整路径
查找数组是否是另一个数组的子集
检查给定的数组是否不相交

6、图（有向图和无向图）

无向图和有向图的建立和遍历，利用邻接矩阵和邻接链表
图的广度优先搜索和深度优先搜索、BFS、DFS