NBER:人群异质化传染病模型中的差异化隔离策略 | 唧唧堂论文解析
picture from Internet
专栏介绍
![]()
长按二维码直接进入专栏
本文为唧唧堂《新冠病毒主题论文导读专栏》内一篇论文解析,唧唧堂将在本专栏收录发布所有新冠病毒主题的经济金融社会心理等社科类论文解析导读,同时也或将收录部分医学论文。
本专栏论文收录无截止时限,现已有超100篇NBER工作论文解析中,未来唧唧堂将源源不断把发现的新冠病毒主题论文放入本专栏,期待各位研究人的关注与订阅。点击了解专栏!
唧唧堂现招募更多经济金融研究人加入写作小组,以更快完成本专栏内容的解析产出,解析作者在获得固定稿费同时,还将获得付费阅读收入的部分提成。点击加入写作小组!
本文是针对工作论文《OPTIMAL TARGETED LOCKDOWNS IN A MULTI-GROUP SIR MODEL(人群异质化传染病模型中的差异化隔离策略)》的一篇解析(NBER Working Paper 27102)。该论文作者是Daron Acemoglu、Victor Chernozhukov、Iván Werning和Michael D. Whinston。
研究背景与问题
现阶段,研究应对COVID-19的政策及其经济影响的宏观理论文献主要应用的方法比较单一——大多数是以价值函数和基本的传染病模型相结合,解一个最优控制问题。这类文献所解决的问题也万变不离其宗——隔离的经济成本与患病/死亡的经济损失之间的权衡。然而,Glenn Ellison等经济学家指出,这些模型存在一系列问题:一是没有考虑到潜在的异质性,譬如老年人患病后的死亡率高于年轻人、不同地区检测患者的能力不同等;二是衡量死亡造成的经济损失的方式始终有待商榷——人生命的价值显然很难确定 [Avery,2020]。[Acemoglu et al., 2020]这篇文章从这两个方面入手,对现有的研究方法进行了改进:(1)为了考虑异质性的影响,这篇文章对传统的传染病(SIR)模型进行了修改,提出了MG-SIR模型(Multi-Group SIR),以分组的方式迈出解决异质性问题的第一步;(2)针对死亡的代价争议巨大这个问题,本文索性不再计算最优解,而是将死亡和隔离产生的经济成本投射到两个维度上,再计算帕累托前线(Pareto Frontier)——不管计划者更关注人命还是更关注金钱,他的最优结果都可以在这条帕累托前线上找到,类似于下图这样
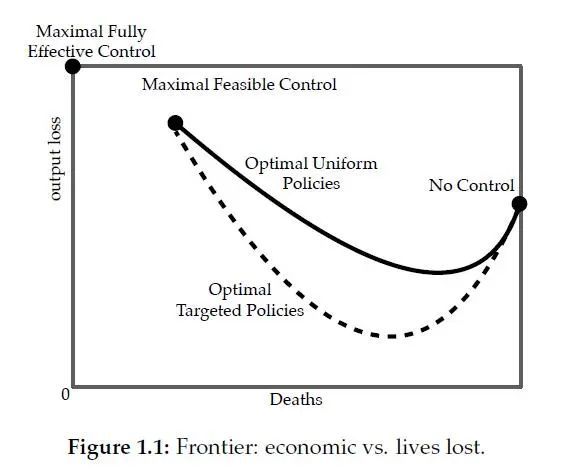
这张图可以算作对本论文主要结论的一处管窥。从其中读者可以直观看出相对于均一的隔离政策而言,分组异质化的隔离政策会将整个帕累托前线向好的方向移动——也就是说,不论社会计划者如何权衡经济损失和死亡率,异质化的隔离政策都能比均一化隔离政策更好地达到其政策目标。(注意:在这幅图中越往左下角移动达到的结果越好,原点为极乐点(bliss point))
模型
模型假设
1. 人群动态转化
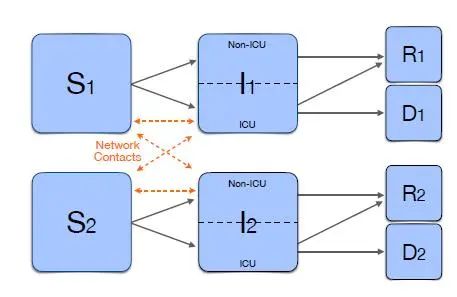
假设模型中个体的交互如上图所示:人们被分为若干组,比如1和2两组,每一组可能都有被感染的人(I)和易感人群(S)。那么整个疫情中,一个人从S变到I可以是因为跟组内或组外不同状态的I接触;而I分为轻症(Non-ICU)和重症(ICU)两种状态(假设每一个S在变成I时成为重症的概率是常数ι[iota],而1-ι的人则为轻症)。重症患者每一时刻有δ^r的概率康复,δ^d的概率死亡(相当于两个独立的泊松分布,下同);轻症患者不会死亡,其康复的泊松率为γ。考虑ICU供给量有限,即内生化死亡率和治愈率,定义ICU的需求量为所有组重症患者之和,以H(t)表示。进而,δ^d死亡率可以表示为关于H(t)的一个非减函数。
2. 检测
假设检测并不是完美的。对于感染患者而言,有一部分人可能不能被检出,定义这部分比例为η;对于康复的患者而言,假设有κ的部分不能被识别,从而潜在的隔离政策可能会对他们进行无谓的隔离(假设康复者能够对病毒完全免疫)。
3. 封城、隔离和经济成本
组j中的个体在单位时间内可以生产w_j的产出。当1个单位(最严格)的隔离措施实施时,该个体单位时间内可以生产(1-ξ_j)w_j的产出(相当于在家仍能完成一部分工作)。定义L_j(t)为t时刻在对组j中的所有人施加的隔离措施的强度(介于0和一个小于1的上限之间),隔离的有效程度为θ_j,那么隔离系数可表示为1-θ_jL_j(t)——可以理解为组j中有“1-θ_jL_j(t)”比例的人,单位时间内的产出为上述被削弱的产出“(1-ξ_j)w_j”,而其余人的产出仍然为“w_j”。
4. 疫苗和特效药
假设在某确定的时刻T疫苗和特效药会同时出现,前者可以使所有易感人群都免疫,而后者可以使所有患者都痊愈。
模型主体
1. MG-SIR模型
考虑连续时间t∈[0,∞], 将总人群分为不同风险的组j = 1, …, J, 每个组有初始成员测度N_j。总人数标准化为1,即∑N_j = 1。在任何时刻t,每个组之内的成员都会被分为四个状态:易感 (S)、感染 (I)、康复 (R)、死亡 (D),并且有如下关系:
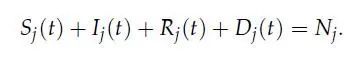
下面,我们将定义疫情传播过程中的动态变化。在传统的模型中,每一时刻新感染的人数往往由下式简单决定
然而本文对此处的处理更为一般化,如果不考虑隔离政策,有
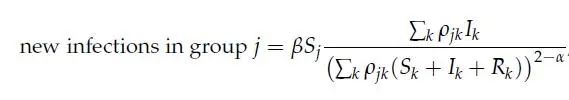
上式也就是组j新增感染者的速率。式中的ρ_jk表示组j和k之间的接触率;α∈[1,2],表示人群密度对人群接触率的影响程度——α=2则为传统模型中的“二次接触”,即接触率与两个相互接触的群体的比例之积成正比(考虑βSI);α=1则为“一次接触”,即接触率与两个相互接触的群体的比例之积的平方根成正比。实际上在现实环境中,公共交通、购物、外出就餐等活动更接近于二次接触,而上班、朋友会面等更接近于一次接触。因此,实际情况中的α值应当介于1和2 之间。
至此,我们可以正式列出MG-SIR模型中各项状态量的动态变化:

其中M是前述动态关系的分母部分:
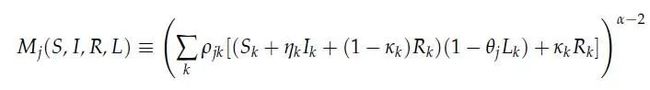
其他的状态量:
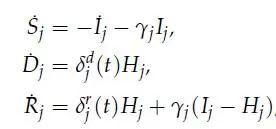
注意,当α=2时,M恒等于1,则I的动态变化变成传统SIR描述的那样:

在此模型中,我们按患病后的死亡率将人群分为三组:青年、中年和老年。
2. 经济与优化目标
社会计划者面临的优化问题如下:为人群中的每一个组选择相应的隔离-时间路径L_j(t),使得经济成本和死亡数量两方面损失最小化。因此这将是一个二维的问题,社会计划者解出的不再是最优点,而是一条经济成本和死亡数量相权衡的帕累托前线。其中,死亡数量简单定义为截至疫苗出现时因疫情死亡的总人数;而经济损失定义如下:
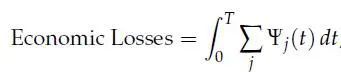
其中ψ为每组的流成本(flow cost):
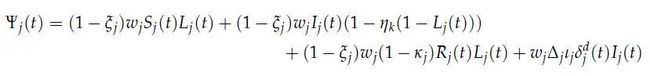
用于表示隔离措施带来的单位时间内(因为工作效率降低造成的)经济损失。
