剑指offer刷题记录(已更19题)
二刷剑指offer,第一遍的基本都忘了,总结一下。
| 题型 | |
| 查找 | 1 6 |
| 字符串 | 2 44 |
| 链表 | 3 |
| 树 | 4 17 |
| 队列 栈 | 5 |
| 递归 | 7 |
1.二维数组中的查找
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
分析:二维数组每行依次递增,每列依次递增。如果从二维数组左上角开始判断,当查找值大于此值,查找值可能在左上角值右侧,也可能在左上角值下方,所以直接从左上角开始判断不能保证接下来查找的方向。思考如果从右上角开始判断呢?显然可以发现如果右上角左侧值都小于它,右上角下侧都大于它。如果查找值大于右上角,那么它只能出现在最后一列;如果小于它,那么只能出现在非最后列,所以依次判断每列最上方元素就可以。
完整代码
public class Solution {
public boolean Find(int target, int [][] array) {
if (array == null) return false;
int row = 0, col = array[0].length - 1;
while (row < array.length && col >= 0){
if (array[row][col] == target)
return true;
else if (array[row][col] > target)
col--;
else
row++;
}
return false;
}
}2.替换空格
实现一个函数,将一个字符串中的每个空格替换成“%20”。例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。
法一:分析将空格转换成%20会让空格后所有的值都向后移动两个位置。最先想到遍历一次得到一共有多少空格,若一共有n个空格则字符串长度会增大2*n,如本题原来长度为12,替换后长度应为12+2*2=16,容易想到应重后向前遍历数组,若不为空格,则arr[i+2*n]=arr[i],若为空格i减去1、arr[i+2*n+2]='0'、arr[i+2*n+1]='2'、arr[i+2*n]='%'。
完整代码
public class Solution {
public String replaceSpace(StringBuffer str) {
if (str == null || str.length() == 0) return "";
int len = str.length();
int count = 0;
for(int i = 0; i=0; i--){
if(str.charAt(i) != ' '){
str.setCharAt(i+count*2,str.charAt(i));
}else{
count--;
str.setCharAt(i+count*2,'%');
str.setCharAt(i+count*2+1,'2');
str.setCharAt(i+count*2+2,'0');
}
}
return str.toString();
}
} 法二:设置一个变长字符串(StringBuffer)作为输出,遍历原字符串,如果为空格追加"%20",如果不为空格追加遍历到的字符。
public class Solution {
public String replaceSpace(StringBuffer str) {
if(str==null) return "";
char[] ch=str.toString().toCharArray();
StringBuffer ret = new StringBuffer();
for(int i=0;i法三:字符串替换。
public class Solution {
public String replaceSpace(StringBuffer str) {
return str.toString().replaceAll("\\s", "%20");
}
}3.从头到尾打印链表
输入一个链表,按链表从尾到头的顺序返回一个ArrayList。
法一:翻转链表,再遍历一遍列表输出到ArrayList中。空间复杂度O(n),时间复杂度O(n)。
import java.util.ArrayList;
public class Solution {
public ArrayList printListFromTailToHead(ListNode listNode) {
ListNode head = null;
ListNode pre = listNode;
ListNode cur = null;
while(pre != null){
cur = pre;
pre = pre.next;
cur.next = head;
head = cur;
}
ArrayList ret = new ArrayList<>();
while(head != null){
ret.add(head.val);
head = head.next;
}
return ret;
}
} 法二:栈——遍历链表,每遍历到一个元素就压入栈中,最后将栈中元素依次弹出添加到ArrayList中,时间复杂度O(n),空间复杂度O(n)
import java.util.ArrayList;
import java.util.Stack;
public class Solution {
public ArrayList printListFromTailToHead(ListNode listNode) {
ArrayList arr = new ArrayList<>();
if(listNode == null) return arr;
Stack sta = new Stack<>();
while(listNode != null){
sta.push(listNode.val);
listNode = listNode.next;
}
while(!sta.isEmpty()){
arr.add(sta.pop());
}
return arr;
}
} 4.重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
思路:重建二叉树,树的问题一般考虑递归解答。考虑已经到最后一步,只要将此序列构建成树。
根据前序遍历的性质,数组中第一个元素必然就是root,那么下面的工作就是如何确定root的左右子树的范围。
根据中序遍历的性质,root元素前面都是root的左子树,后面都是root的右子树。那么我们只要找到中序遍历中root的位置,就可以确定好左右子树的范围。
正如上面所说,只需要将确定的左右子树安到root上即可。递归要注意出口,假设最后只有一个元素了,那么就要返回。
public class Solution {
public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
TreeNode root=reConstructBinaryTree(pre,0,pre.length-1,in,0,in.length-1);
return root;
}
//前序遍历{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}
private TreeNode reConstructBinaryTree(int [] pre,int startPre,int endPre,int [] in,int startIn,int endIn) {
if(startPre>endPre||startIn>endIn)
return null;
TreeNode root=new TreeNode(pre[startPre]);
//在中序遍历中找到分割左右子树的位置(即前序遍历中首个元素位置)
for(int i=startIn;i<=endIn;i++)
if(in[i]==pre[startPre]){
//安装右子树,i-startIn即右子树长度,startPre+i-startIn即前序遍历左子树尾部。
root.left=reConstructBinaryTree(pre,startPre+1,startPre+i-startIn,in,startIn,i-1);
//安装左子树
root.right=reConstructBinaryTree(pre,i-startIn+startPre+1,endPre,in,i+1,endIn);
break;
}
return root;
}
}优化写法:使用HashMap,键为数值,值是此值在中序遍历位置。
获取中序遍历分割位置只需在HashMap中读即可。
import java.util.HashMap;
import java.util.Map;
public class Solution {
Map map = new HashMap<>();
public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
if (pre == null || in == null ||pre.length==0) return null;
for(int i=0;iright) return null;
TreeNode root = new TreeNode(pre[left]);
int tap = map.get(pre[left]);
int left_len = tap - cur;
root.left = reConstruct(pre, left+1, left+left_len, cur);
root.right = reConstruct(pre, left+left_len+1, right, tap+1);
return root;
}
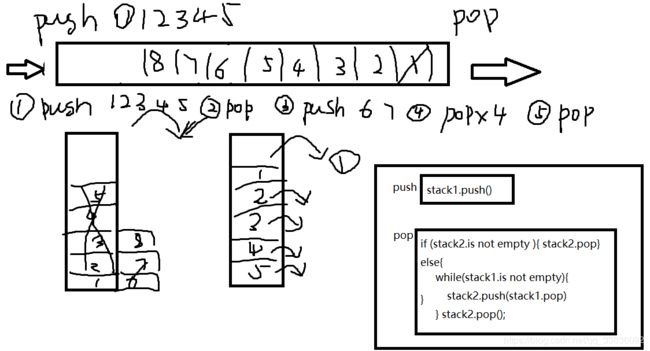
} 5.用两个栈实现队列
import java.util.Stack;
public class Solution {
Stack stack1 = new Stack();
Stack stack2 = new Stack();
public void push(int node) {
stack1.push(node);
}
public int pop() {
if (!stack2.isEmpty()){
return stack2.pop();
}else{
while (!stack1.isEmpty()){
stack2.push(stack1.pop());
}
return stack2.pop();
}
}
} 优化一下:
import java.util.Stack;
public class Solution {
Stack stack1 = new Stack();
Stack stack2 = new Stack();
public void push(int node) {
stack1.push(node);
}
public int pop() {
if (stack2.isEmpty())
while (!stack1.isEmpty())
stack2.push(stack1.pop());
return stack2.pop();
}
} 6.旋转数组中最小数字
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。
NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
import java.util.ArrayList;
public class Solution {
public int minNumberInRotateArray(int [] array) {
if(array == null || array.length==0) return 0;
int low = 0;
int high = array.length-1;
//旋转之后前面数组元素 大于 后面数组元素。low值为前面最小值,high值为后面最大值
if(array[low]7.斐波那契数列
大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0,第1项是1)。
n<=39
public class Solution {
public int Fibonacci(int n) {
if (n <= 1) return n;
int[] fib = new int[n+1];
fib[1] = 1;
fib[0] = 0;
for (int i = 2; i <= n; i++)
fib[i] = fib[i - 1] + fib[i - 2];
return fib[n];
}
}考虑到第 i 项只与第 i-1 和第 i-2 项有关,因此只需要存储前两项的值就能求解第 i 项,从而将空间复杂度由 O(N) 降低为 O(1)。
public int Fibonacci(int n) {
if (n <= 1)
return n;
int pre2 = 0, pre1 = 1;
int fib = 0;
for (int i = 2; i <= n; i++) {
fib = pre2 + pre1;
pre2 = pre1;
pre1 = fib;
}
return fib;
}8.跳台阶
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
public class Solution {
public int JumpFloor(int target) {
if (target <= 2) return target;
int[] fib = new int[target+1];
fib[1] = 1;
fib[2] = 2;
for (int i = 3; i <= target; i++)
fib[i] = fib[i - 1] + fib[i - 2];
return fib[target];
}
}将空间复杂度由 O(N) 降低为 O(1)。
public class Solution {
public int JumpFloor(int target) {
if (target <= 2) return target;
int pre2=1,pre1=2;
int fib = 0;
for(int i=3; i<=target; i++){
fib = pre2+pre1;
pre2 = pre1;
pre1 = fib;
}
return fib;
}
}9.变态跳台阶
f(n) = 2*f(n-1)
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
public class Solution {
public int JumpFloorII(int target) {
if(target<=2) return target;
int f=1,fn=1;
for(int i=2;i<=target;i++){
fn = 2*f;
f = fn;
}
return fn;
}
}位移操作:
public class Solution {
public int JumpFloorII(int target) {
return 1<<(target-1);
}
}
17.树的子结构
输入两棵二叉树A,B,判断B是不是A的子结构。(ps:我们约定空树不是任意一个树的子结构)
public class Solution {
public boolean HasSubtree(TreeNode root1,TreeNode root2) {
if(root1 == null || root2 == null) return false;
boolean result = false;
if(root1.val == root2.val) result = HasSubtreeCore(root1,root2);
if(!result) result = HasSubtree(root1.left,root2);
if(!result) result = HasSubtree(root1.right,root2);
return result;
}
private boolean HasSubtreeCore(TreeNode root1,TreeNode root2){
if (root2 == null) return true;
if (root1 == null) return false;
if (root1.val != root2.val) return false;
return HasSubtreeCore(root1.right,root2.right) && HasSubtreeCore(root1.left,root2.left);
}
}19.二叉树的镜像
操作给定的二叉树,将其变换为源二叉树的镜像。
二叉树的镜像定义:源二叉树
8
/ \
6 10
/ \ / \
5 7 9 11
镜像二叉树
8
/ \
10 6
/ \ / \
11 9 7 5public class Solution {
public void Mirror(TreeNode root) {
if(root==null) return;
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
Mirror(root.right);
Mirror(root.left);
}
}
22.从上往下打印二叉树
从上往下打印出二叉树的每个节点,同层节点从左至右打印。
import java.util.ArrayList;
import java.util.Queue;
import java.util.LinkedList;
public class Solution {
public ArrayList PrintFromTopToBottom(TreeNode root) {
ArrayList ret = new ArrayList<>();
Queue q = new LinkedList<>();
if(root == null) return ret;
q.offer(root);
while(!q.isEmpty()){
TreeNode temp = q.poll();
ret.add(temp.val);
if(temp.left != null)
q.offer(temp.left);
if(temp.right != null)
q.offer(temp.right);
}
return ret;
}
} 23.二叉搜索树的后序遍历序列
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
public class Solution {
public boolean VerifySquenceOfBST(int [] sequence) {
if (sequence == null || sequence.length==0) return false;
return verify(sequence,0,sequence.length-1);
}
private boolean verify(int[] sequence,int first,int last){
if (first >= last) return true;
int temp = sequence[last];
int cut = first;
while(cut24.二叉树中和为某一值的路径
输入一颗二叉树的根节点和一个整数,按字典序打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
import java.util.ArrayList;
public class Solution {
private ArrayList> ret = new ArrayList<>();
public ArrayList> FindPath(TreeNode root,int target) {
FindPathCore(root,target,new ArrayList<>());
return ret;
}
private void FindPathCore(TreeNode node,int target,ArrayList path){
if(node == null) return;
path.add(node.val);
target -= node.val;
if(target==0 && node.left==null && node.right==null){
ret.add(new ArrayList<>(path));
}else if(target<0){
// 小于0 删除该点,
}else{
// 大于0 或者等于0并且为0时有子节点(子节点有值可能为0)。继续向下找
FindPathCore(node.left,target,path);
FindPathCore(node.right,target,path);
}
//该点在路径中所有情况已分析完,从路径中删除该点
path.remove(path.size()-1);
}
} 26.二叉搜索树与双向链表
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
public class Solution {
private TreeNode pre = null;
private TreeNode head = null;
public TreeNode Convert(TreeNode pRootOfTree) {
// 对这棵树使用中序遍历连接后为顺序的双向链表。
inOrder(pRootOfTree);
return head;
}
private void inOrder(TreeNode node){
if (node == null) return;
inOrder(node.left);
if(pre == null){
pre = node;
head = node;
}else{
pre.right = node;
node.left = pre;
pre = node;
}
inOrder(node.right);
}
}38.二叉树的深度
输入一棵二叉树,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。
import java.lang.Math;
public class Solution {
public int TreeDepth(TreeNode root) {
if (root == null) return 0;
int left = TreeDepth(root.left);
int right = TreeDepth(root.right);
return Math.max(left+1,right+1);
}
}39.平衡二叉树
输入一棵二叉树,判断该二叉树是否是平衡二叉树。
在这里,我们只需要考虑其平衡性,不需要考虑其是不是排序二叉树
结合38题,对每个节点判断左子树和右子树差是否小于等于1。
public class Solution {
public boolean IsBalanced_Solution(TreeNode root) {
if(root == null) return true;
return Math.abs(depth(root.left) - depth(root.right))<=1 &&
IsBalanced_Solution(root.left) && IsBalanced_Solution(root.right);
}
private int depth(TreeNode root){
if(root == null) return 0;
return 1 + Math.max(depth(root.left), depth(root.right));
}
}这种做法有很明显的问题,在判断上层结点的时候,会多次重复遍历下层结点,增加了不必要的开销。如果改为从下往上遍历,如果子树是平衡二叉树,则返回子树的高度;如果发现子树不是平衡二叉树,则直接停止遍历,这样至多只对每个结点访问一次。
public class Solution {
public boolean IsBalanced_Solution(TreeNode root) {
return getDepth(root) != -1;
}
private int getDepth(TreeNode root) {
if (root == null) return 0;
int left = getDepth(root.left);
if (left == -1) return -1;
int right = getDepth(root.right);
if (right == -1) return -1;
return Math.abs(left - right) > 1 ? -1 : 1 + Math.max(left, right);
}
}44.翻转单词顺序
牛客最近来了一个新员工Fish,每天早晨总是会拿着一本英文杂志,写些句子在本子上。同事Cat对Fish写的内容颇感兴趣,有一天他向Fish借来翻看,但却读不懂它的意思。例如,“student. a am I”。后来才意识到,这家伙原来把句子单词的顺序翻转了,正确的句子应该是“I am a student.”。Cat对一一的翻转这些单词顺序可不在行,你能帮助他么?
public class Solution {
public String ReverseSentence(String str) {
String[] s = str.split(" ");
if (s.length == 0) return str;
StringBuffer ret = new StringBuffer();
for(int i = s.length-1;i>=0;i--){
if(i==0)
ret.append(s[i]);
else
ret.append(s[i]+" ");
}
return ret.toString();
}
}
64.滑动窗口的最大值
优先队列实现大顶堆
第一中解法——优先队列 PriorityQueue,优先队列实现大顶堆,注意(o1,o2)->(o2-o1)
import java.util.ArrayList;
import java.util.PriorityQueue;
public class Solution {
public ArrayList maxInWindows(int [] num, int size)
{
ArrayList ret = new ArrayList<>();
int len = num.length;
if (num == null || len == 0 || size < 1 || len < size) return ret;
//构造大顶堆 大顶堆顶部元素始终为最大元素。
PriorityQueue maxHeap = new PriorityQueue((o1,o2)->(o2-o1));
//将前size个元素输入到大顶堆中。并将最大值添加到输出中
for (int i = 0; i 第二种方法双端队列
假设k为3,
[4,2,5] 对于这个序列2永远不可能在输出队列中因为,2小于5
[4,2,1]对于这个序列2可能出现在输出队列中因为它后面元素为1,当[2,1,1]时2可能在输出队列中
假设有队列[6,7,2,1,8,3,9] 输出队列为[7,7,8,8,9]
7入队,6再无作用相当于队列中只有[7]
2入队,7依然有作用
假设每入队一个元素就会将它之前小于它的元素删除。
[7]-->[7,2]--->[7,2,1]--->[8]---->[8,3]--->[9]
发现队首元素始终为最大值,但第一个7不应该输出,因为此时入队的元素数量还没到size.
import java.util.LinkedList;
import java.util.ArrayList;
public class Solution {
public ArrayList maxInWindows(int [] num, int size)
{
ArrayList ret = new ArrayList<>();
//双端队列,用来记录每个窗口的最大值下标
LinkedList de = new LinkedList<>();
if(size<=0 || num==null || num.length==0) return ret;
for(int i=0;inum[de.peekLast()]){
de.pollLast();
}
de.addLast(i);
//判断队首元素是否过期
if(de.peekFirst()==i-size)
de.pollFirst();
//向result列表中加入元素
if(i>=size-1)
ret.add(num[de.peekFirst()]);
}
return ret;
}
}