排序算法介绍讲解（冒泡排序，插入排序，选择排序，归并排序，快速排序，堆排序）及其Python代码实现

ps: 以下的笔记摘抄整理自极客时间，侵删

排序

基于比较的排序算法的执行过程，会涉及两种操作，一种是元素比较大小，另一种是元素交换或移动。所以，如果我们在分析排序算法的执行效率的时候，应该把比较次数和交换（或移动）次数也考虑进去。

1 冒泡排序

冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求。如果不满足就让它俩互换。

Python代码实现如下：

def bubble(arr):
    # 遍历所有的元素
    for i in range(len(arr)):
        # 比对还未排好序的相邻元素（注意要减i,i为橙红色排好序的元素）
        for j in range(len(arr)-i -1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr

2 插入排序

取未排序区间中的元素，在已排序区间中找到合适的插入位置将其插入，并保证已排序区间数据一直有序

Python代码实现如下：

def insertionSort(arr):
    # 第一轮比较后，最小值在最左侧，左侧为排序好的数字
    for i in range(1, len(arr)):
        # 记录当前比较数字的位置，之后与这个数字之前的数字（左边的数字）进行比较
        key = arr[i]

        # 与当前的前一位数字进行比较
        j = i - 1
        #
        while j >= 0 and key < arr[j]:  # 初始key为a[j+1]的值
            arr[j + 1] = arr[j]  # 左侧的值依次比较 
            j -= 1
        arr[j + 1] = key
    return arr

3 选择排序

：

选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

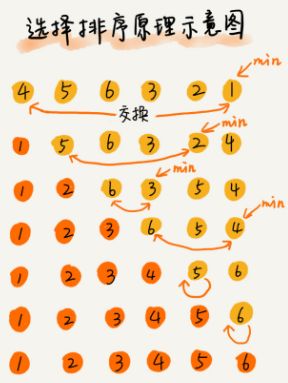
Python代码实现：

def slect_sort(A):
    for i in range(len(A)):
        # 保存最小值的位置
        min_idx = i
        for j in range(i + 1, len(A)):
            # 找到最小值的位置
            if A[min_idx] > A[j]:
                min_idx = j

        A[i], A[min_idx] = A[min_idx], A[i]
    return A

插入排序与冒泡排序的区别：
假如均为从小到大排序，插入排序在第一轮比较结束后，最小值排在最左边。而冒泡排序在第一轮比较结束后，最大值排在最右边。都是比较相邻元素，交换相邻位置的元素。

4 归并排序

如果要排序一个数组，我们先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了

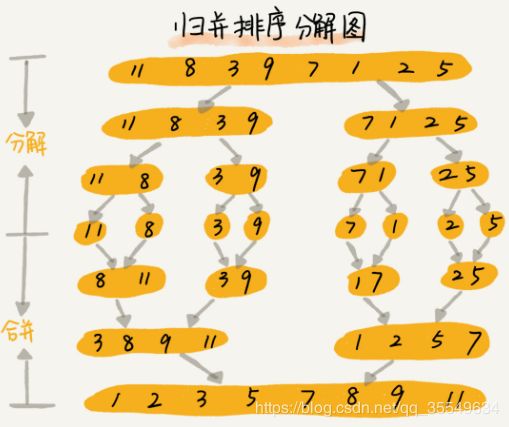
伪代码实现：

// 归并排序算法, A是数组，n表示数组大小
merge_sort(A, n) {
  merge_sort_c(A, 0, n-1)
}

// 递归调用函数
merge_sort_c(A, p, r) {
  // 递归终止条件
  if p >= r  then return

  // 取p到r之间的中间位置q
  q = (p+r) / 2
  // 分治递归
  merge_sort_c(A, p, q)
  merge_sort_c(A, q+1, r)
  // 将A[p...q]和A[q+1...r]合并为A[p...r]
  merge(A[p...r], A[p...q], A[q+1...r])
}

伪代码的解释：
merge_sort(p…r) 表示，给下标从 p 到 r 之间的数组排序。我们将这个排序问题转化为了两个子问题，merge_sort(p…q) 和 merge_sort(q+1…r)，其中下标 q 等于 p 和 r 的中间位置，也就是 (p+r)/2。当下标从 p 到 q 和从 q+1 到 r 这两个子数组都排好序之后，我们再将两个有序的子数组合并在一起，这样下标从 p 到 r 之间的数据就也排好序了。
merge(A[p…r], A[p…q], A[q+1…r]) 这个函数的作用就是，将已经有序的 A[p…q]和 A[q+1…r]合并成一个有序的数组，并且放入 A[p…r]

对merge方法，如图所示，我们申请一个临时数组 tmp，大小与 A[p…r]相同。我们用两个游标 i 和 j，分别指向 A[p…q]和 A[q+1…r]的第一个元素。比较这两个元素 A[i]和 A[j]，如果 A[i]<=A[j]，我们就把 A[i]放入到临时数组 tmp，并且 i 后移一位，否则将 A[j]放入到数组 tmp，j 后移一位。
继续上述比较过程，直到其中一个子数组中的所有数据都放入临时数组中，再把另一个数组中的数据依次加入到临时数组的末尾，这个时候，临时数组中存储的就是两个子数组合并之后的结果了。最后再把临时数组 tmp 中的数据拷贝到原数组 A[p…r]中。
对应的图解分析如下：

Python代码实现

def merge(arr, l, m, r):
    n1 = m - l + 1
    n2 = r - m

    # 创建临时数组
    L = [0] * (n1)
    R = [0] * (n2)

    # 拷贝数据到临时数组 arrays L[] 和 R[]
    for i in range(0, n1):
        L[i] = arr[l + i]

    for j in range(0, n2):
        R[j] = arr[m + 1 + j]

        # 归并临时数组到 arr[l..r]
    i = 0  # 初始化第一个子数组的索引
    j = 0  # 初始化第二个子数组的索引
    k = l  # 初始归并子数组的索引

    while i < n1 and j < n2:
        if L[i] <= R[j]:
            arr[k] = L[i]
            i += 1
        else:
            arr[k] = R[j]
            j += 1
        k += 1

    # 拷贝 L[] 的保留元素
    while i < n1:
        arr[k] = L[i]
        i += 1
        k += 1

    # 拷贝 R[] 的保留元素
    while j < n2:
        arr[k] = R[j]
        j += 1
        k += 1


def mergeSort(arr, l, r):
    if l < r:
        m = int((l + (r - 1)) / 2)

        mergeSort(arr, l, m)
        mergeSort(arr, m + 1, r)
        merge(arr, l, m, r)
    print(arr)


if __name__ == "__main__":
    arr = [4, 3, 6, 1, 2]
    mergeSort(arr, 0, len(arr)-1)

5 快排

常见算法面试题

归并排序和快速排序都用到了分治思想，非常巧妙。
我们可以借鉴这个思想，来解决非排序的问题，比如：
（1）如何在 O(n) 的时间复杂度内查找一个无序数组中的第 K 大元素？（快排，归并）
（2）快速找到最大的K个元素？（堆排序）
（3）两个大数相乘（转换为两个字符串相乘，按位相乘）