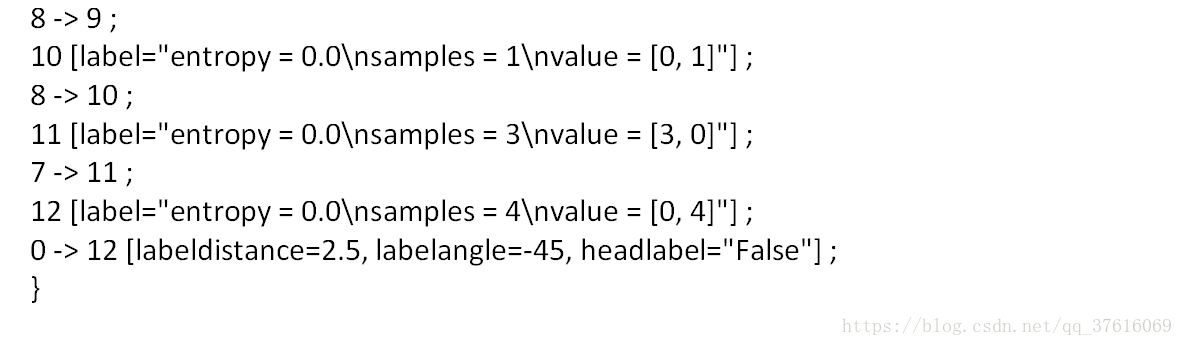机器学习中一些基本的算法源码实现及注释详情
decision_tree的源码实现:
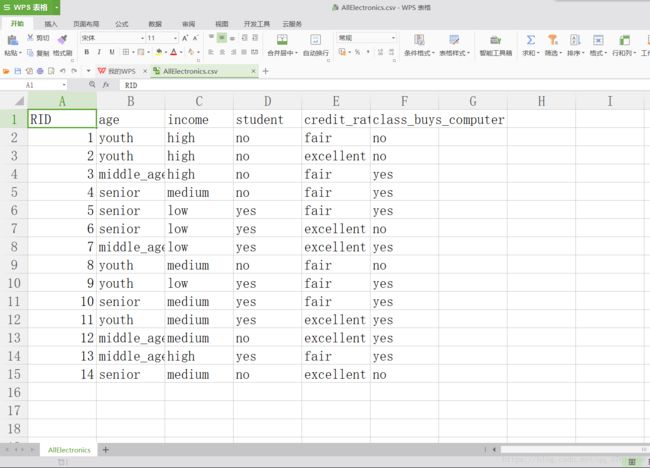
#coding:utf-8 from sklearn.feature_extraction import DictVectorizer import csv from sklearn import preprocessing from sklearn import tree from sklearn.externals.six import StringIO # 读取csv数据 data = open(r'F:\study\code\python\machine_learning\decision_tree\AllElectronics.csv', 'rb') # csv.reader可以按行读取内容 # csv_reader把每一行数据转化成了一个list,list中每个元素是一个字符串。 reader = csv.reader(data) headers = reader.next() # print(headers) # 装取feature,即特征值的informatiom featureLIst = [] # 存储最后一行的值 labelList = [] for Row in reader: # 每一个Row表示表格中的一行 # print(Row) # labelList中存储的是每一行的最后一个值 labelList.append(Row[len(Row) - 1]) # RowDict存储的是从age到credit_rating的值 RowDict = {} # 接着遍历每一行里面的特征值 for i in range(1, len(Row) - 1): # print(Row[i]) # RowDict的key对应的就是从每一行中取出来的值 RowDict[headers[i]] = Row[i] # print("RowDict:" + RowDict) featureLIst.append(RowDict) # 输出的应该是一个list of dictionary,之所以转换为这种形式是为了便于利用python中的模块,可以把这种list of dictionary转换成0-1的格式 print(featureLIst) # 实例化,DicVectorizer是一个对象 vec = DictVectorizer() # 转换成我们需要的dummy variable格式 dummyX = vec.fit_transform(featureLIst).toarray() print("dummyX:" + str(dummyX)) print(vec.get_feature_names()) print ("labelList:" + str(labelList)) # 在python中提供了一种把class labels转换成0-1格式的方法 lb = preprocessing.LabelBinarizer() dummyY = lb.fit_transform(labelList) print ("dummyY:" + str(dummyY)) # 利用sklearn创建决策树 # criterion='entropy'指的是利用信息熵为标准创建决策树 clf = tree.DecisionTreeClassifier(criterion='entropy') clf = clf.fit(dummyX, dummyY) print("clf:" + str(clf)) # 将决策树可视化,保存为dot文件 with open("allElectronicInformationGainOri.dot", "w") as f: f = tree.export_graphviz(clf, feature_names=vec.get_feature_names(), out_file=f) # 原表格中第一行的数据 oneRowX = dummyX[0, :] print("oneRowX:" + str(oneRowX)) # 将第一行的数据修改年纪:youth->middle_aged,然后进行测试 newRowX = oneRowX newRowX[0] = 1 newRowX[2] = 0 print("newRowX:" + str(newRowX)) predictedY = clf.predict(newRowX) print("predictedY: " + str(predictedY))
csv_file:
dot文件:
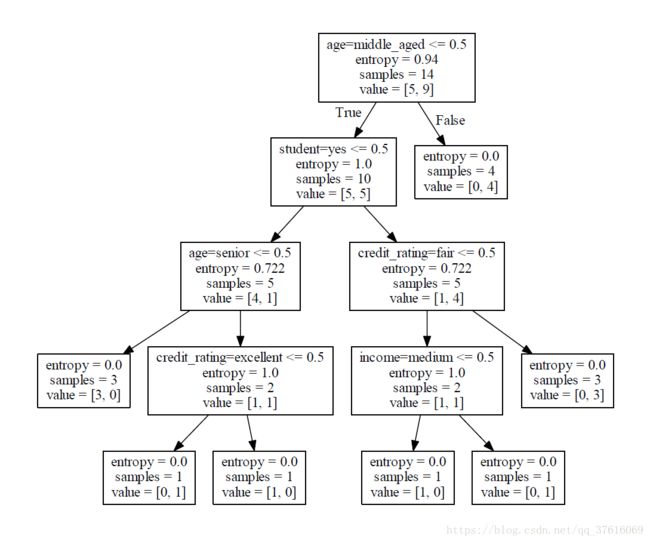
pdf文件:
K_means算法:
源码:
# coding:utf-8 from numpy import * """ Code for hierarchical clustering, modified from Programming Collective Intelligence by Toby Segaran (O'Reilly Media 2007, page 33). """ # 结点定义 class cluster_node: def __init__(self, vec, left=None, right=None, distance=0.0, id=None, count=1): self.left = left self.right = right self.vec = vec self.id = id self.distance = distance self.count = count # only used for weighted average # 求两种不同距离的方法 def L2dist(v1, v2): return sqrt(sum((v1 - v2) ** 2)) def L1dist(v1, v2): return sum(abs(v1 - v2)) # def Chi2dist(v1,v2): # return sqrt(sum((v1-v2)**2)) def hcluster(features, distance=L2dist): # cluster the rows of the "features" matrix distances = {} currentclustid = -1 # clusters are initially just the individual rows clust = [cluster_node(array(features[i]), id=i) for i in range(len(features))] while len(clust) > 1: lowestpair = (0, 1) closest = distance(clust[0].vec, clust[1].vec) # loop through every pair looking for the smallest distance for i in range(len(clust)): for j in range(i + 1, len(clust)): # distances is the cache of distance calculations if (clust[i].id, clust[j].id) not in distances: distances[(clust[i].id, clust[j].id)] = distance(clust[i].vec, clust[j].vec) d = distances[(clust[i].id, clust[j].id)] if d < closest: closest = d lowestpair = (i, j) # calculate the average of the two clusters mergevec = [(clust[lowestpair[0]].vec[i] + clust[lowestpair[1]].vec[i]) / 2.0 \ for i in range(len(clust[0].vec))] # create the new cluster newcluster = cluster_node(array(mergevec), left=clust[lowestpair[0]], right=clust[lowestpair[1]], distance=closest, id=currentclustid) # cluster ids that weren't in the original set are negative currentclustid -= 1 del clust[lowestpair[1]] del clust[lowestpair[0]] clust.append(newcluster) return clust[0] def extract_clusters(clust, dist): # extract list of sub-tree clusters from hcluster tree with distanceclusters = {} if clust.distance < dist: # we have found a cluster subtree return [clust] else: # check the right and left branches cl = [] cr = [] if clust.left != None: cl = extract_clusters(clust.left, dist=dist) if clust.right != None: cr = extract_clusters(clust.right, dist=dist) return cl + cr def get_cluster_elements(clust): # return ids for elements in a cluster sub-tree if clust.id >= 0: # positive id means that this is a leaf return [clust.id] else: # check the right and left branches cl = [] cr = [] if clust.left != None: cl = get_cluster_elements(clust.left) if clust.right != None: cr = get_cluster_elements(clust.right) return cl + cr def printclust(clust, labels=None, n=0): # indent to make a hierarchy layout for i in range(n): print ' ', if clust.id < 0: # negative id means that this is branch print '-' else: # positive id means that this is an endpoint if labels == None: print clust.id else: print labels[clust.id] # now print the right and left branches if clust.left != None: printclust(clust.left, labels=labels, n=n + 1) if clust.right != None: printclust(clust.right, labels=labels, n=n + 1) def getheight(clust): # Is this an endpoint? Then the height is just 1 if clust.left == None and clust.right == None: return 1 # Otherwise the height is the same of the heights of # each branch return getheight(clust.left) + getheight(clust.right) def getdepth(clust): # The distance of an endpoint is 0.0 if clust.left == None and clust.right == None: return 0 # The distance of a branch is the greater of its two sides # plus its own distance return max(getdepth(clust.left), getdepth(clust.right)) + clust.distance
实例测试源码:
# coding:utf-8 import numpy as np def k_means(X, K, maxIt): """ :param x: 数据集 :param k: 分类数目 :param maxIt: 最大迭代更新次数 """ # numPoints表示行数,numDim表示列数(维度) numPoints, numDim = X.shape # 新建一个数据集,比X多一列,用于存储分类 dataSet = np.zeros((numPoints, numDim + 1)) dataSet[:, : -1] = X # 随机选取K个中心点作为初始化的中心点 centroids = dataSet[np.random.randint(numPoints, size=K), :] # centroids = dataSet[0:2, :] # 给中心点的最后一列随机赋值 centroids[:, -1] = range(1, K + 1) # iterations :循环次数 iterations = 0 oldCentroids = None # Run the main k-means algorithm while not shouldStop(oldCentroids, centroids, iterations, maxIt): print "iteration: \n", iterations print "dataSet: \n", dataSet print "centroids: \n", centroids # Save old centroids for convergence test. Book keeping. # 使用np.copy()改变一个的值不会影响另外一个的值,即两个变量不指向同一内存空间 oldCentroids = np.copy(centroids) iterations += 1 # Assign labels to each datapoint based on centroids # 更新分类标签 updateLabels(dataSet, centroids) # Assign centroids based on datapoint labels # 更新中心点 centroids = getCentroids(dataSet, K) # We can get the labels too by calling getLabels(dataSet, centroids) return dataSet # Function: Should Stop # ------------- # Returns True or False if k-means is done. K-means terminates either # because it has run a maximum number of iterations OR the centroids # stop changing. def shouldStop(oldCentroids, centroids, iterations, maxIt): if iterations > maxIt: return True # 比较两者值是否相等 return np.array_equal(oldCentroids, centroids) # Function: Get Labels # ------------- # Update a label for each piece of data in the dataset. def updateLabels(dataSet, centroids): # For each element in the dataset, chose the closest centroid. # Make that centroid the element's label. numPoints, numDim = dataSet.shape for i in range(0, numPoints): dataSet[i, -1] = getLabelFromClosestCentroid(dataSet[i, :-1], centroids) def getLabelFromClosestCentroid(dataSetRow, centroids): label = centroids[0, -1]; minDist = np.linalg.norm(dataSetRow - centroids[0, :-1]) for i in range(1, centroids.shape[0]): # np.linalg.norm用于计算距离 dist = np.linalg.norm(dataSetRow - centroids[i, :-1]) if dist < minDist: minDist = dist label = centroids[i, -1] print "minDist:", minDist return label # Function: Get Centroids # ------------- # Returns k random centroids, each of dimension n. def getCentroids(dataSet, k): # Each centroid is the geometric mean of the points that # have that centroid's label. Important: If a centroid is empty (no points have # that centroid's label) you should randomly re-initialize it. result = np.zeros((k, dataSet.shape[1])) for i in range(1, k + 1): oneCluster = dataSet[dataSet[:, -1] == i, :-1] """ mean()函数功能:求取均值 经常操作的参数为axis,以m * n矩阵举例: axis 不设置值,对 m*n 个数求均值,返回一个实数 axis = 0:压缩行,对各列求均值,返回 1* n 矩阵 axis =1 :压缩列,对各行求均值,返回 m *1 矩阵 """ result[i - 1, :-1] = np.mean(oneCluster, axis=0) result[i - 1, -1] = i return result x1 = np.array([1, 1]) x2 = np.array([2, 1]) x3 = np.array([4, 3]) x4 = np.array([5, 4]) # 把四个点纵向排列,组成一个矩阵 testX = np.vstack((x1, x2, x3, x4)) result = k_means(testX, 2, 10) print "final result:" print result
运行结果:
iteration:
0
dataSet:
[[1. 1. 0.]
[2. 1. 0.]
[4. 3. 0.]
[5. 4. 0.]]
centroids:
[[4. 3. 1.]
[5. 4. 2.]]
minDist: 3.60555127546
minDist: 2.82842712475
minDist: 0.0
minDist: 0.0
iteration:
1
dataSet:
[[1. 1. 1.]
[2. 1. 1.]
[4. 3. 1.]
[5. 4. 2.]]
centroids:
[[2.33333333 1.66666667 1. ]
[5. 4. 2. ]]
minDist: 1.490711985
minDist: 0.7453559925
minDist: 1.41421356237
minDist: 0.0
iteration:
2
dataSet:
[[1. 1. 1.]
[2. 1. 1.]
[4. 3. 2.]
[5. 4. 2.]]
centroids:
[[1.5 1. 1. ]
[4.5 3.5 2. ]]
minDist: 0.5
minDist: 0.5
minDist: 0.707106781187
minDist: 0.707106781187
final result:
[[1. 1. 1.]
[2. 1. 1.]
[4. 3. 2.]
[5. 4. 2.]]
进程已结束,退出代码0
KMN算法:
# coding:utf-8 # 读取数据 import csv import random import math # operator模块提供的itemgetter函数用于获取对象的哪些维的数据,参数为一些序号 # operator.itemgetter函数获取的不是值,而是定义了一个函数,通过该函数作用到对象上才能获取值。 import operator # 装载数据集 def loadDataset(filename, split, trainingSet = [], testSet = []): """ filename: 需要装载的数据集路径及名称 split: 将数据集分为两部分----trainingSet和testSet trainingSet: 训练集 testSet: 测试集 """ with open(filename, "rb") as csvfile: # 读取所有的行 lines = csv.reader(csvfile) # 转化为list的数据结构 dataset = list(lines) # dataset的格式是列表中存在列表的格式,列表中的每一个子列表表示原数据中的一行数据 # print "dataset的格式:", dataset # 把数据集分为两部分,分别装到训练集和测试集里面去 # x表示行 for x in range(len(dataset) - 1): for y in range(4): dataset[x][y] = float(dataset[x][y]) # random.random()的范围是[0, 1) if random.random() < split: trainingSet.append(dataset[x]) else: testSet.append(dataset[x]) print "trainingSet", trainingSet print "testSet", testSet # 计算EuclideanDistance # 参数为两个实例以及维度,返回值是euclideanDistance # pow()平方,sqrt()开方 def euclideanDistance(instance1, instance2, length): distance = 0 for x in range(length): distance += pow((instance1[x] - instance2[x]), 2) return math.sqrt(distance) # 返回离目标点最近的K个点 # testInstance指的是测试集中的一个实例(数据) def getNeighbors(trainingSet, testInstance, k): # 初始化distances作为容器装所有的距离 distances = [] # length指的是测试实例的维度 length = len(testInstance) - 1 # 计算测试实例到训练集中各点的距离的列表集合 for x in range(len(trainingSet)): dist = euclideanDistance(testInstance, trainingSet[x], length) distances.append((trainingSet[x], dist)) # 此时distances的格式[([5.1, 3.5, 1.4, 0.2, 'Iris-setosa'], 4.459820624195552), ([4.9, 3.0, 1.4, 0.2, 'Iris-setosa'], 4.498888751680798),。。。] # print "distances列表:", distances # 此处key=operator.itemgetter(1)的作用是根据第2个域(距离)进行排序,默认为升序 distances.sort(key=operator.itemgetter(1)) neighbors = [] # 取前k个距离最近的点 for x in range(k): neighbors.append(distances[x][0]) # print "neighbors:", neighbors # neighbors: [[6.5, 3.2, 5.1, 2.0, 'Iris-virginica'], [6.7, 3.3, 5.7, 2.5, 'Iris-virginica'],[6.5, 3.0, 5.8, 2.2, 'Iris-virginica']] return neighbors # 在K个点中,根据少数服从多数原则,将目标点进行归类 def getResponse(neighbors): classVotes = {} for x in range(len(neighbors)): # neighbors[x][-1]指的是距离最近的每一种花的品种 response = neighbors[x][-1] # 统计距离最近的花里面每一品种的个数 if response in classVotes: classVotes[response] += 1 else: classVotes[response] = 1 # reverse参数,是一个bool变量,表示升序还是降序排列,默认为false(升序排列),定义为True时将按降序排列 sortedNotes = sorted(classVotes.iteritems(), key=operator.itemgetter(1), reverse=True) return sortedNotes[0][0] # 测试准确率 def getAccuracy(testSet, predictions): correct = 0 for x in range(len(testSet)): # -1指的是最后一个值,也就是花的类别 if testSet[x][-1] == predictions[x]: correct += 1 return (correct/float(len(testSet))) * 100.0 # 主函数 def main(): trainingSet = [] testSet = [] # 0.67的作用:把2/3的数据划分为训练集,把1/3的数据划分为测试集 split = 0.67 # 调用loadDataset函数 loadDataset(r'F:\study\code\python\machine_learning\KNN\irisdata.txt', split, trainingSet, testSet) # repr() 转化为供解释器读取的形式。 print 'TrainSet: ' + repr(len(trainingSet)) print 'TestSet: ' + repr(len(testSet)) # generate predictions predictions = [] k = 3 for x in range(len(testSet)): neighbors = getNeighbors(trainingSet, testSet[x], k) result = getResponse(neighbors) predictions.append(result) print("> predicted= " + repr(result) + ', actual=' + repr(testSet[x][-1])) # 准确率 accuracy = getAccuracy(testSet, predictions) print("Accuracy: " + repr(accuracy) + "%") if __name__ == '__main__': main()
运行结果:
trainingSet [[5.1, 3.5, 1.4, 0.2, 'Iris-setosa'], [4.9, 3.0, 1.4, 0.2, 'Iris-setosa'], [4.6, 3.4, 1.4, 0.3, 'Iris-setosa'], [5.0, 3.4, 1.5, 0.2, 'Iris-setosa'], [4.4, 2.9, 1.4, 0.2, 'Iris-setosa'], [5.4, 3.7, 1.5, 0.2, 'Iris-setosa'], [4.8, 3.4, 1.6, 0.2, 'Iris-setosa'], [4.3, 3.0, 1.1, 0.1, 'Iris-setosa'], [5.8, 4.0, 1.2, 0.2, 'Iris-setosa'], [5.4, 3.9, 1.3, 0.4, 'Iris-setosa'], [5.1, 3.5, 1.4, 0.3, 'Iris-setosa'], [5.7, 3.8, 1.7, 0.3, 'Iris-setosa'], [5.1, 3.8, 1.5, 0.3, 'Iris-setosa'], [4.6, 3.6, 1.0, 0.2, 'Iris-setosa'], [5.1, 3.3, 1.7, 0.5, 'Iris-setosa'], [4.8, 3.4, 1.9, 0.2, 'Iris-setosa'], [5.0, 3.4, 1.6, 0.4, 'Iris-setosa'], [5.2, 3.5, 1.5, 0.2, 'Iris-setosa'], [5.2, 3.4, 1.4, 0.2, 'Iris-setosa'], [4.7, 3.2, 1.6, 0.2, 'Iris-setosa'], [4.8, 3.1, 1.6, 0.2, 'Iris-setosa'], [5.2, 4.1, 1.5, 0.1, 'Iris-setosa'], [5.5, 4.2, 1.4, 0.2, 'Iris-setosa'], [4.9, 3.1, 1.5, 0.1, 'Iris-setosa'], [5.5, 3.5, 1.3, 0.2, 'Iris-setosa'], [4.4, 3.0, 1.3, 0.2, 'Iris-setosa'], [5.1, 3.4, 1.5, 0.2, 'Iris-setosa'], [5.0, 3.5, 1.3, 0.3, 'Iris-setosa'], [4.5, 2.3, 1.3, 0.3, 'Iris-setosa'], [4.4, 3.2, 1.3, 0.2, 'Iris-setosa'], [5.0, 3.5, 1.6, 0.6, 'Iris-setosa'], [5.1, 3.8, 1.9, 0.4, 'Iris-setosa'], [5.1, 3.8, 1.6, 0.2, 'Iris-setosa'], [4.6, 3.2, 1.4, 0.2, 'Iris-setosa'], [5.0, 3.3, 1.4, 0.2, 'Iris-setosa'], [6.9, 3.1, 4.9, 1.5, 'Iris-versicolor'], [5.5, 2.3, 4.0, 1.3, 'Iris-versicolor'], [6.5, 2.8, 4.6, 1.5, 'Iris-versicolor'], [5.7, 2.8, 4.5, 1.3, 'Iris-versicolor'], [4.9, 2.4, 3.3, 1.0, 'Iris-versicolor'], [5.2, 2.7, 3.9, 1.4, 'Iris-versicolor'], [5.0, 2.0, 3.5, 1.0, 'Iris-versicolor'], [5.9, 3.0, 4.2, 1.5, 'Iris-versicolor'], [6.1, 2.9, 4.7, 1.4, 'Iris-versicolor'], [5.6, 2.9, 3.6, 1.3, 'Iris-versicolor'], [6.7, 3.1, 4.4, 1.4, 'Iris-versicolor'], [5.6, 3.0, 4.5, 1.5, 'Iris-versicolor'], [5.8, 2.7, 4.1, 1.0, 'Iris-versicolor'], [6.2, 2.2, 4.5, 1.5, 'Iris-versicolor'], [5.6, 2.5, 3.9, 1.1, 'Iris-versicolor'], [6.1, 2.8, 4.0, 1.3, 'Iris-versicolor'], [6.1, 2.8, 4.7, 1.2, 'Iris-versicolor'], [6.4, 2.9, 4.3, 1.3, 'Iris-versicolor'], [6.6, 3.0, 4.4, 1.4, 'Iris-versicolor'], [6.8, 2.8, 4.8, 1.4, 'Iris-versicolor'], [6.7, 3.0, 5.0, 1.7, 'Iris-versicolor'], [5.7, 2.6, 3.5, 1.0, 'Iris-versicolor'], [5.5, 2.4, 3.8, 1.1, 'Iris-versicolor'], [5.5, 2.4, 3.7, 1.0, 'Iris-versicolor'], [5.4, 3.0, 4.5, 1.5, 'Iris-versicolor'], [6.0, 3.4, 4.5, 1.6, 'Iris-versicolor'], [6.7, 3.1, 4.7, 1.5, 'Iris-versicolor'], [6.3, 2.3, 4.4, 1.3, 'Iris-versicolor'], [5.6, 3.0, 4.1, 1.3, 'Iris-versicolor'], [5.5, 2.5, 4.0, 1.3, 'Iris-versicolor'], [6.1, 3.0, 4.6, 1.4, 'Iris-versicolor'], [5.7, 2.9, 4.2, 1.3, 'Iris-versicolor'], [6.2, 2.9, 4.3, 1.3, 'Iris-versicolor'], [5.1, 2.5, 3.0, 1.1, 'Iris-versicolor'], [5.8, 2.7, 5.1, 1.9, 'Iris-virginica'], [7.1, 3.0, 5.9, 2.1, 'Iris-virginica'], [7.6, 3.0, 6.6, 2.1, 'Iris-virginica'], [4.9, 2.5, 4.5, 1.7, 'Iris-virginica'], [7.3, 2.9, 6.3, 1.8, 'Iris-virginica'], [6.5, 3.2, 5.1, 2.0, 'Iris-virginica'], [6.4, 2.7, 5.3, 1.9, 'Iris-virginica'], [5.7, 2.5, 5.0, 2.0, 'Iris-virginica'], [6.4, 3.2, 5.3, 2.3, 'Iris-virginica'], [7.7, 3.8, 6.7, 2.2, 'Iris-virginica'], [7.7, 2.6, 6.9, 2.3, 'Iris-virginica'], [7.7, 2.8, 6.7, 2.0, 'Iris-virginica'], [6.3, 2.7, 4.9, 1.8, 'Iris-virginica'], [6.7, 3.3, 5.7, 2.1, 'Iris-virginica'], [7.2, 3.2, 6.0, 1.8, 'Iris-virginica'], [6.2, 2.8, 4.8, 1.8, 'Iris-virginica'], [6.4, 2.8, 5.6, 2.1, 'Iris-virginica'], [7.2, 3.0, 5.8, 1.6, 'Iris-virginica'], [7.4, 2.8, 6.1, 1.9, 'Iris-virginica'], [7.9, 3.8, 6.4, 2.0, 'Iris-virginica'], [6.4, 2.8, 5.6, 2.2, 'Iris-virginica'], [7.7, 3.0, 6.1, 2.3, 'Iris-virginica'], [6.3, 3.4, 5.6, 2.4, 'Iris-virginica'], [6.4, 3.1, 5.5, 1.8, 'Iris-virginica'], [6.0, 3.0, 4.8, 1.8, 'Iris-virginica'], [6.9, 3.1, 5.4, 2.1, 'Iris-virginica'], [6.7, 3.1, 5.6, 2.4, 'Iris-virginica'], [6.8, 3.2, 5.9, 2.3, 'Iris-virginica'], [6.7, 3.3, 5.7, 2.5, 'Iris-virginica'], [6.7, 3.0, 5.2, 2.3, 'Iris-virginica'], [6.3, 2.5, 5.0, 1.9, 'Iris-virginica'], [6.5, 3.0, 5.2, 2.0, 'Iris-virginica'], [6.2, 3.4, 5.4, 2.3, 'Iris-virginica']]
testSet [[4.7, 3.2, 1.3, 0.2, 'Iris-setosa'], [4.6, 3.1, 1.5, 0.2, 'Iris-setosa'], [5.0, 3.6, 1.4, 0.2, 'Iris-setosa'], [5.4, 3.9, 1.7, 0.4, 'Iris-setosa'], [4.9, 3.1, 1.5, 0.1, 'Iris-setosa'], [4.8, 3.0, 1.4, 0.1, 'Iris-setosa'], [5.7, 4.4, 1.5, 0.4, 'Iris-setosa'], [5.4, 3.4, 1.7, 0.2, 'Iris-setosa'], [5.1, 3.7, 1.5, 0.4, 'Iris-setosa'], [5.0, 3.0, 1.6, 0.2, 'Iris-setosa'], [5.4, 3.4, 1.5, 0.4, 'Iris-setosa'], [5.0, 3.2, 1.2, 0.2, 'Iris-setosa'], [4.9, 3.1, 1.5, 0.1, 'Iris-setosa'], [4.8, 3.0, 1.4, 0.3, 'Iris-setosa'], [5.3, 3.7, 1.5, 0.2, 'Iris-setosa'], [7.0, 3.2, 4.7, 1.4, 'Iris-versicolor'], [6.4, 3.2, 4.5, 1.5, 'Iris-versicolor'], [6.3, 3.3, 4.7, 1.6, 'Iris-versicolor'], [6.6, 2.9, 4.6, 1.3, 'Iris-versicolor'], [6.0, 2.2, 4.0, 1.0, 'Iris-versicolor'], [5.9, 3.2, 4.8, 1.8, 'Iris-versicolor'], [6.3, 2.5, 4.9, 1.5, 'Iris-versicolor'], [6.0, 2.9, 4.5, 1.5, 'Iris-versicolor'], [5.8, 2.7, 3.9, 1.2, 'Iris-versicolor'], [6.0, 2.7, 5.1, 1.6, 'Iris-versicolor'], [5.5, 2.6, 4.4, 1.2, 'Iris-versicolor'], [5.8, 2.6, 4.0, 1.2, 'Iris-versicolor'], [5.0, 2.3, 3.3, 1.0, 'Iris-versicolor'], [5.6, 2.7, 4.2, 1.3, 'Iris-versicolor'], [5.7, 3.0, 4.2, 1.2, 'Iris-versicolor'], [5.7, 2.8, 4.1, 1.3, 'Iris-versicolor'], [6.3, 3.3, 6.0, 2.5, 'Iris-virginica'], [6.3, 2.9, 5.6, 1.8, 'Iris-virginica'], [6.5, 3.0, 5.8, 2.2, 'Iris-virginica'], [6.7, 2.5, 5.8, 1.8, 'Iris-virginica'], [7.2, 3.6, 6.1, 2.5, 'Iris-virginica'], [6.8, 3.0, 5.5, 2.1, 'Iris-virginica'], [5.8, 2.8, 5.1, 2.4, 'Iris-virginica'], [6.5, 3.0, 5.5, 1.8, 'Iris-virginica'], [6.0, 2.2, 5.0, 1.5, 'Iris-virginica'], [6.9, 3.2, 5.7, 2.3, 'Iris-virginica'], [5.6, 2.8, 4.9, 2.0, 'Iris-virginica'], [6.1, 3.0, 4.9, 1.8, 'Iris-virginica'], [6.3, 2.8, 5.1, 1.5, 'Iris-virginica'], [6.1, 2.6, 5.6, 1.4, 'Iris-virginica'], [6.9, 3.1, 5.1, 2.3, 'Iris-virginica'], [5.8, 2.7, 5.1, 1.9, 'Iris-virginica']]TrainSet: 102
TestSet: 47
> predicted= 'Iris-setosa', actual='Iris-setosa'
> predicted= 'Iris-setosa', actual='Iris-setosa'
> predicted= 'Iris-setosa', actual='Iris-setosa'
> predicted= 'Iris-setosa', actual='Iris-setosa'
> predicted= 'Iris-setosa', actual='Iris-setosa'
> predicted= 'Iris-setosa', actual='Iris-setosa'
> predicted= 'Iris-setosa', actual='Iris-setosa'
> predicted= 'Iris-setosa', actual='Iris-setosa'
> predicted= 'Iris-setosa', actual='Iris-setosa'
> predicted= 'Iris-setosa', actual='Iris-setosa'
> predicted= 'Iris-setosa', actual='Iris-setosa'
> predicted= 'Iris-setosa', actual='Iris-setosa'
> predicted= 'Iris-setosa', actual='Iris-setosa'
> predicted= 'Iris-setosa', actual='Iris-setosa'
> predicted= 'Iris-setosa', actual='Iris-setosa'
> predicted= 'Iris-versicolor', actual='Iris-versicolor'
> predicted= 'Iris-versicolor', actual='Iris-versicolor'
> predicted= 'Iris-versicolor', actual='Iris-versicolor'
> predicted= 'Iris-versicolor', actual='Iris-versicolor'
> predicted= 'Iris-versicolor', actual='Iris-versicolor'
> predicted= 'Iris-virginica', actual='Iris-versicolor'
> predicted= 'Iris-virginica', actual='Iris-versicolor'
> predicted= 'Iris-versicolor', actual='Iris-versicolor'
> predicted= 'Iris-versicolor', actual='Iris-versicolor'
> predicted= 'Iris-virginica', actual='Iris-versicolor'
> predicted= 'Iris-versicolor', actual='Iris-versicolor'
> predicted= 'Iris-versicolor', actual='Iris-versicolor'
> predicted= 'Iris-versicolor', actual='Iris-versicolor'
> predicted= 'Iris-versicolor', actual='Iris-versicolor'
> predicted= 'Iris-versicolor', actual='Iris-versicolor'
> predicted= 'Iris-versicolor', actual='Iris-versicolor'
> predicted= 'Iris-virginica', actual='Iris-virginica'
> predicted= 'Iris-virginica', actual='Iris-virginica'
> predicted= 'Iris-virginica', actual='Iris-virginica'
> predicted= 'Iris-virginica', actual='Iris-virginica'
> predicted= 'Iris-virginica', actual='Iris-virginica'
> predicted= 'Iris-virginica', actual='Iris-virginica'
> predicted= 'Iris-virginica', actual='Iris-virginica'
> predicted= 'Iris-virginica', actual='Iris-virginica'
> predicted= 'Iris-versicolor', actual='Iris-virginica'
> predicted= 'Iris-virginica', actual='Iris-virginica'
> predicted= 'Iris-virginica', actual='Iris-virginica'
> predicted= 'Iris-virginica', actual='Iris-virginica'
> predicted= 'Iris-virginica', actual='Iris-virginica'
> predicted= 'Iris-virginica', actual='Iris-virginica'
> predicted= 'Iris-virginica', actual='Iris-virginica'
> predicted= 'Iris-virginica', actual='Iris-virginica'
Accuracy: 91.48936170212765%
进程已结束,退出代码0
KMN第二种实现方法:直接利用sklearn中的相关方法实现:
# coding:utf-8 from sklearn import neighbors from sklearn import datasets # 创建一个名为knn的分类器 knn = neighbors.KNeighborsClassifier() iris = datasets.load_iris() print iris # 建立模型,第一个参数代表特征值的矩阵,第二个参数代表每一行对应的分类 knn.fit(iris.data, iris.target) # 预测一个花的品种 predictedLabel = knn.predict([[0.1, 0.2, 0.3, 0.4]]) print predictedLabel
运行结果:
{'target_names': array(['setosa', 'versicolor', 'virginica'], dtype='|S10'), 'data': array([[5.1, 3.5, 1.4, 0.2],
[4.9, 3. , 1.4, 0.2],
[4.7, 3.2, 1.3, 0.2],
[4.6, 3.1, 1.5, 0.2],
[5. , 3.6, 1.4, 0.2],
[5.4, 3.9, 1.7, 0.4],
[4.6, 3.4, 1.4, 0.3],
[5. , 3.4, 1.5, 0.2],
[4.4, 2.9, 1.4, 0.2],
[4.9, 3.1, 1.5, 0.1],
[5.4, 3.7, 1.5, 0.2],
[4.8, 3.4, 1.6, 0.2],
[4.8, 3. , 1.4, 0.1],
[4.3, 3. , 1.1, 0.1],
[5.8, 4. , 1.2, 0.2],
[5.7, 4.4, 1.5, 0.4],
[5.4, 3.9, 1.3, 0.4],
[5.1, 3.5, 1.4, 0.3],
[5.7, 3.8, 1.7, 0.3],
[5.1, 3.8, 1.5, 0.3],
[5.4, 3.4, 1.7, 0.2],
[5.1, 3.7, 1.5, 0.4],
[4.6, 3.6, 1. , 0.2],
[5.1, 3.3, 1.7, 0.5],
[4.8, 3.4, 1.9, 0.2],
[5. , 3. , 1.6, 0.2],
[5. , 3.4, 1.6, 0.4],
[5.2, 3.5, 1.5, 0.2],
[5.2, 3.4, 1.4, 0.2],
[4.7, 3.2, 1.6, 0.2],
[4.8, 3.1, 1.6, 0.2],
[5.4, 3.4, 1.5, 0.4],
[5.2, 4.1, 1.5, 0.1],
[5.5, 4.2, 1.4, 0.2],
[4.9, 3.1, 1.5, 0.1],
[5. , 3.2, 1.2, 0.2],
[5.5, 3.5, 1.3, 0.2],
[4.9, 3.1, 1.5, 0.1],
[4.4, 3. , 1.3, 0.2],
[5.1, 3.4, 1.5, 0.2],
[5. , 3.5, 1.3, 0.3],
[4.5, 2.3, 1.3, 0.3],
[4.4, 3.2, 1.3, 0.2],
[5. , 3.5, 1.6, 0.6],
[5.1, 3.8, 1.9, 0.4],
[4.8, 3. , 1.4, 0.3],
[5.1, 3.8, 1.6, 0.2],
[4.6, 3.2, 1.4, 0.2],
[5.3, 3.7, 1.5, 0.2],
[5. , 3.3, 1.4, 0.2],
[7. , 3.2, 4.7, 1.4],
[6.4, 3.2, 4.5, 1.5],
[6.9, 3.1, 4.9, 1.5],
[5.5, 2.3, 4. , 1.3],
[6.5, 2.8, 4.6, 1.5],
[5.7, 2.8, 4.5, 1.3],
[6.3, 3.3, 4.7, 1.6],
[4.9, 2.4, 3.3, 1. ],
[6.6, 2.9, 4.6, 1.3],
[5.2, 2.7, 3.9, 1.4],
[5. , 2. , 3.5, 1. ],
[5.9, 3. , 4.2, 1.5],
[6. , 2.2, 4. , 1. ],
[6.1, 2.9, 4.7, 1.4],
[5.6, 2.9, 3.6, 1.3],
[6.7, 3.1, 4.4, 1.4],
[5.6, 3. , 4.5, 1.5],
[5.8, 2.7, 4.1, 1. ],
[6.2, 2.2, 4.5, 1.5],
[5.6, 2.5, 3.9, 1.1],
[5.9, 3.2, 4.8, 1.8],
[6.1, 2.8, 4. , 1.3],
[6.3, 2.5, 4.9, 1.5],
[6.1, 2.8, 4.7, 1.2],
[6.4, 2.9, 4.3, 1.3],
[6.6, 3. , 4.4, 1.4],
[6.8, 2.8, 4.8, 1.4],
[6.7, 3. , 5. , 1.7],
[6. , 2.9, 4.5, 1.5],
[5.7, 2.6, 3.5, 1. ],
[5.5, 2.4, 3.8, 1.1],
[5.5, 2.4, 3.7, 1. ],
[5.8, 2.7, 3.9, 1.2],
[6. , 2.7, 5.1, 1.6],
[5.4, 3. , 4.5, 1.5],
[6. , 3.4, 4.5, 1.6],
[6.7, 3.1, 4.7, 1.5],
[6.3, 2.3, 4.4, 1.3],
[5.6, 3. , 4.1, 1.3],
[5.5, 2.5, 4. , 1.3],
[5.5, 2.6, 4.4, 1.2],
[6.1, 3. , 4.6, 1.4],
[5.8, 2.6, 4. , 1.2],
[5. , 2.3, 3.3, 1. ],
[5.6, 2.7, 4.2, 1.3],
[5.7, 3. , 4.2, 1.2],
[5.7, 2.9, 4.2, 1.3],
[6.2, 2.9, 4.3, 1.3],
[5.1, 2.5, 3. , 1.1],
[5.7, 2.8, 4.1, 1.3],
[6.3, 3.3, 6. , 2.5],
[5.8, 2.7, 5.1, 1.9],
[7.1, 3. , 5.9, 2.1],
[6.3, 2.9, 5.6, 1.8],
[6.5, 3. , 5.8, 2.2],
[7.6, 3. , 6.6, 2.1],
[4.9, 2.5, 4.5, 1.7],
[7.3, 2.9, 6.3, 1.8],
[6.7, 2.5, 5.8, 1.8],
[7.2, 3.6, 6.1, 2.5],
[6.5, 3.2, 5.1, 2. ],
[6.4, 2.7, 5.3, 1.9],
[6.8, 3. , 5.5, 2.1],
[5.7, 2.5, 5. , 2. ],
[5.8, 2.8, 5.1, 2.4],
[6.4, 3.2, 5.3, 2.3],
[6.5, 3. , 5.5, 1.8],
[7.7, 3.8, 6.7, 2.2],
[7.7, 2.6, 6.9, 2.3],
[6. , 2.2, 5. , 1.5],
[6.9, 3.2, 5.7, 2.3],
[5.6, 2.8, 4.9, 2. ],
[7.7, 2.8, 6.7, 2. ],
[6.3, 2.7, 4.9, 1.8],
[6.7, 3.3, 5.7, 2.1],
[7.2, 3.2, 6. , 1.8],
[6.2, 2.8, 4.8, 1.8],
[6.1, 3. , 4.9, 1.8],
[6.4, 2.8, 5.6, 2.1],
[7.2, 3. , 5.8, 1.6],
[7.4, 2.8, 6.1, 1.9],
[7.9, 3.8, 6.4, 2. ],
[6.4, 2.8, 5.6, 2.2],
[6.3, 2.8, 5.1, 1.5],
[6.1, 2.6, 5.6, 1.4],
[7.7, 3. , 6.1, 2.3],
[6.3, 3.4, 5.6, 2.4],
[6.4, 3.1, 5.5, 1.8],
[6. , 3. , 4.8, 1.8],
[6.9, 3.1, 5.4, 2.1],
[6.7, 3.1, 5.6, 2.4],
[6.9, 3.1, 5.1, 2.3],
[5.8, 2.7, 5.1, 1.9],
[6.8, 3.2, 5.9, 2.3],
[6.7, 3.3, 5.7, 2.5],
[6.7, 3. , 5.2, 2.3],
[6.3, 2.5, 5. , 1.9],
[6.5, 3. , 5.2, 2. ],
[6.2, 3.4, 5.4, 2.3],
[5.9, 3. , 5.1, 1.8]]), 'target': array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]), 'DESCR': 'Iris Plants Database\n====================\n\nNotes\n-----\nData Set Characteristics:\n :Number of Instances: 150 (50 in each of three classes)\n :Number of Attributes: 4 numeric, predictive attributes and the class\n :Attribute Information:\n - sepal length in cm\n - sepal width in cm\n - petal length in cm\n - petal width in cm\n - class:\n - Iris-Setosa\n - Iris-Versicolour\n - Iris-Virginica\n :Summary Statistics:\n\n ============== ==== ==== ======= ===== ====================\n Min Max Mean SD Class Correlation\n ============== ==== ==== ======= ===== ====================\n sepal length: 4.3 7.9 5.84 0.83 0.7826\n sepal width: 2.0 4.4 3.05 0.43 -0.4194\n petal length: 1.0 6.9 3.76 1.76 0.9490 (high!)\n petal width: 0.1 2.5 1.20 0.76 0.9565 (high!)\n ============== ==== ==== ======= ===== ====================\n\n :Missing Attribute Values: None\n :Class Distribution: 33.3% for each of 3 classes.\n :Creator: R.A. Fisher\n :Donor: Michael Marshall (MARSHALL%[email protected])\n :Date: July, 1988\n\nThis is a copy of UCI ML iris datasets.\nhttp://archive.ics.uci.edu/ml/datasets/Iris\n\nThe famous Iris database, first used by Sir R.A Fisher\n\nThis is perhaps the best known database to be found in the\npattern recognition literature. Fisher\'s paper is a classic in the field and\nis referenced frequently to this day. (See Duda & Hart, for example.) The\ndata set contains 3 classes of 50 instances each, where each class refers to a\ntype of iris plant. One class is linearly separable from the other 2; the\nlatter are NOT linearly separable from each other.\n\nReferences\n----------\n - Fisher,R.A. "The use of multiple measurements in taxonomic problems"\n Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to\n Mathematical Statistics" (John Wiley, NY, 1950).\n - Duda,R.O., & Hart,P.E. (1973) Pattern Classification and Scene Analysis.\n (Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.\n - Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System\n Structure and Classification Rule for Recognition in Partially Exposed\n Environments". IEEE Transactions on Pattern Analysis and Machine\n Intelligence, Vol. PAMI-2, No. 1, 67-71.\n - Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule". IEEE Transactions\n on Information Theory, May 1972, 431-433.\n - See also: 1988 MLC Proceedings, 54-64. Cheeseman et al"s AUTOCLASS II\n conceptual clustering system finds 3 classes in the data.\n - Many, many more ...\n', 'feature_names': ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']}
[0]
进程已结束,退出代码0
NeuralNetwork算法:
源码:
# coding:utf-8 import numpy as np # 下载数据集 from sklearn.datasets import load_digits # 通过矩阵显示结果 from sklearn.metrics import confusion_matrix, classification_report # 转换数字0-9的数据类型为python可接受的数据类型 from sklearn.preprocessing import LabelBinarizer from neuralNetwork import NeuralNetwork # 数据集拆分为训练集和测试集 from sklearn.model_selection import train_test_split digits = load_digits() X = digits.data y = digits.target # print X # print y X -= X.min() X /= X.max() # print X # print y nn = NeuralNetwork([64, 100, 10], 'logistic') X_train, X_test, y_train, y_test = train_test_split(X, y) label_train = LabelBinarizer().fit_transform(y_train) lable_test = LabelBinarizer().fit_transform(y_test) print 'start fitting' nn.fit(X_train, label_train, epochs=3000) predictions = [] for i in range(X_test.shape[0]): o = nn.predict(X_test[i]) predictions.append(np.argmax(o)) print confusion_matrix(y_test, predictions) print classification_report(y_test, predictions)
运行结果:
start fitting
[[41 0 0 0 2 0 0 0 0 0]
[ 0 39 0 0 0 0 0 0 0 2]
[ 0 0 31 0 0 0 0 0 0 0]
[ 0 1 2 37 0 0 0 0 2 0]
[ 0 4 0 0 47 0 0 0 1 0]
[ 0 0 0 0 1 41 0 0 0 4]
[ 0 2 0 0 0 0 43 0 1 0]
[ 0 0 0 0 1 0 0 49 1 1]
[ 0 3 0 0 0 2 0 0 40 2]
[ 0 0 0 0 0 0 0 1 1 48]]
precision recall f1-score support
0 1.00 0.95 0.98 43
1 0.80 0.95 0.87 41
2 0.94 1.00 0.97 31
3 1.00 0.88 0.94 42
4 0.92 0.90 0.91 52
5 0.95 0.89 0.92 46
6 1.00 0.93 0.97 46
7 0.98 0.94 0.96 52
8 0.87 0.85 0.86 47
9 0.84 0.96 0.90 50
avg / total 0.93 0.92 0.93 450
进程已结束,退出代码0
neuralNetWork.py
# coding:utf-8 # numpy库提供了一些基于矩阵的科学运算 import numpy as np # 直接调用numpy库里面的tanh双曲函数 def tanh(x): return np.tanh(x) # 定义tanh的一阶导数函数 # tanh(x)的导数为1-tanh(x)的平方 def tan_deriv(x): return 1.0 - np.tanh(x) * np.tanh(x) # 定义逻辑函数 # exp(x)方法返回值为e的x次方 def logistic(x): return 1/(1 + np.exp(-x)) # 定义逻辑函数 # 逻辑函数f(x)的导数为:f(x)*(1-(f(x)) def logistic_derivative(x): return logistic(x) * (1 - logistic(x)) class NeuralNetwork(): def __init__(self, layers, activation='tanh'): """ \layers: 表示每层有多少神经元,用列表表示 activation: 用户指定采用哪种模式,默认为tanh """ if activation == 'logistic': self.activation = logistic self.activation_deriv = logistic_derivative else: self.activation = tanh self.activation_deriv = tan_deriv self.weights = [] # 对权重进行随机赋值 for i in range(1, len(layers) - 1): self.weights.append((2 * np.random.random((layers[i - 1] + 1, layers[i] + 1)) - 1) * 0.25) self.weights.append((2 * np.random.random((layers[i] + 1, layers[i + 1])) - 1) * 0.25) def fit(self, X, y, learning_rate=0.2, epochs=10000): """ X指的是训练集,每一行对应一个实例,列数表示特征值的维度。y指的是classlabel(分类标记) learn_rate指的是学习率,一般取0.2 epochs指的是利用抽样的方法来更新,训练次数,这里设置为10000次 """ # 将X的数据类型改为numpy,最少是一个二维的数组 X = np.atleast_2d(X) # 初始化一个矩阵,假设X是一个10 x 100的矩阵.X.shape()返回值为(10,100) temp = np.ones([X.shape[0], X.shape[1] + 1]) # 冒号指的是取所有的行,列数从第一列到除了最后一列 temp[:, 0:-1] = X X = temp # y指的是分类标记,数据类型转换 y = np.array(y) for k in range(epochs): i = np.random.randint(X.shape[0]) # a表示随机从X中抽取的一行实例对神经网络进行更新 a = [X[i]] # 正向更新 # going forward network, for each layer for l in range(len(self.weights)): # Computer the node value for each layer (O_i) using activation function a.append(self.activation(np.dot(a[l], self.weights[l]))) # Computer the error at the top layer error = y[i] - a[-1] # For output layer, Err calculation (delta is updated error) deltas = [error * self.activation_deriv(a[-1])] # 反向更新 # we need to begin at the second to last layer for l in range(len(a) - 2, 0, -1): # Compute the updated error (i,e, deltas) for each node going from top layer to input layer deltas.append(deltas[-1].dot(self.weights[l].T) * self.activation_deriv(a[l])) deltas.reverse() for i in range(len(self.weights)): layer = np.atleast_2d(a[i]) delta = np.atleast_2d(deltas[i]) self.weights[i] += learning_rate * layer.T.dot(delta) def predict(self, x): x = np.array(x) temp = np.ones(x.shape[0] + 1) temp[0:-1] = x a = temp for l in range(0, len(self.weights)): a = self.activation(np.dot(a, self.weights[l])) return a
调用neuralNetwork中的NeuralNetwork:
from neuralNetwork import NeuralNetwork import numpy as np nn = NeuralNetwork([2, 2, 1], 'tanh') X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]]) y = np.array([0, 1, 1, 0]) nn.fit(X, y) for i in [[0, 0], [0, 1], [1, 0], [1, 1]]: print i, nn.predict(i)
运行结果:
[0, 0] [-0.00015573]
[0, 1] [0.99842087]
[1, 0] [0.99845495]
[1, 1] [0.03373141]
进程已结束,退出代码0
Regression_Problem(回归问题):
Simple_Regression_problem
# coding:utf-8 import numpy as np # x, y为两个列表 def fitSLR(x, y): n = len(x) # 分母 dinominator = 0 # 分子 numerator = 0 for i in range(0, n): # np.mean()为numpy里面计算均值的方法 numerator += (x[i] - np.mean(x))*(y[i] - np.mean(y)) dinominator += (x[i] - np.mean(x))**2 b1 = numerator/float(dinominator) b0 = np.mean(y)/float(np.mean(x)) return b0, b1 def predict(x, b0, b1): return b0 + x*b1 x = [1, 3, 2, 1, 3] y = [14, 24, 18, 17, 27] b0, b1 = fitSLR(x, y) print "intercept:", b0, " slope:", b1 x_test = 6 y_test = predict(x_test, b0, b1) print "y_test:", y_test
运行结果:
intercept: 10.0 slope: 5.0
y_test: 40.0
进程已结束,退出代码0
计算皮尔逊系数的代码实现:
# coding:utf-8 import numpy as np import math def computeCorrelation(X, Y): # 计算均值 x_bar = np.mean(X) y_bar = np.mean(Y) SSR = 0 varX = 0 varY = 0 for i in range(0, len(X)): diffXx_bar = X[i] - x_bar diffYy_bar = Y[i] - y_bar SSR += (diffXx_bar * diffYy_bar) varX += diffXx_bar ** 2 varY += diffYy_bar ** 2 SST = math.sqrt(varX * varY) return SSR / SST testX = [1, 3, 8, 7, 9] testY = [10, 12, 24, 21, 34] print computeCorrelation(testX, testY)
运行结果:
0.940310076545
进程已结束,退出代码0
计算R的平方值的代码实现:
# coding:utf-8 import numpy as np import math def computeCorrelation(X, Y): # 计算均值 x_bar = np.mean(X) y_bar = np.mean(Y) SSR = 0 varX = 0 varY = 0 for i in range(0, len(X)): diffXx_bar = X[i] - x_bar diffYy_bar = Y[i] - y_bar SSR += (diffXx_bar * diffYy_bar) varX += diffXx_bar ** 2 varY += diffYy_bar ** 2 SST = math.sqrt(varX * varY) return SSR / SST def polyfit(x, y, degree): results = {} # 当传入三个参数之后,自动将回归方程计算出来,返回值为相关系数 # x:自变量 y:因变量 degree表示的是最高次数 coeffs = np.polyfit(x, y, degree) results['polynormol'] = coeffs.tolist() # p相当于直线方程 p = np.poly1d(coeffs) # 计算y_hat yhat = p(x) ybar = np.sum(y)/len(y) ssreg = np.sum((yhat-ybar)**2) print "ssreg: ", ssreg sstot = np.sum((y-ybar)**2) print "sstot: ", sstot results['determination'] = ssreg/sstot return results testX = [1, 3, 8, 7, 9] testY = [10, 12, 24, 21, 34] print "r: ", computeCorrelation(testX, testY) print "R^2: ", str(computeCorrelation(testX, testY)**2) print polyfit(testX, testY, 1)
运行结果:
r: 0.940310076545
R^2: 0.8841830400518192
ssreg: 333.360169492
sstot: 377
{'polynormol': [2.65677966101695, 5.322033898305075], 'determination': 0.8842444814098822}
进程已结束,退出代码0
multiple_Regression_problem:
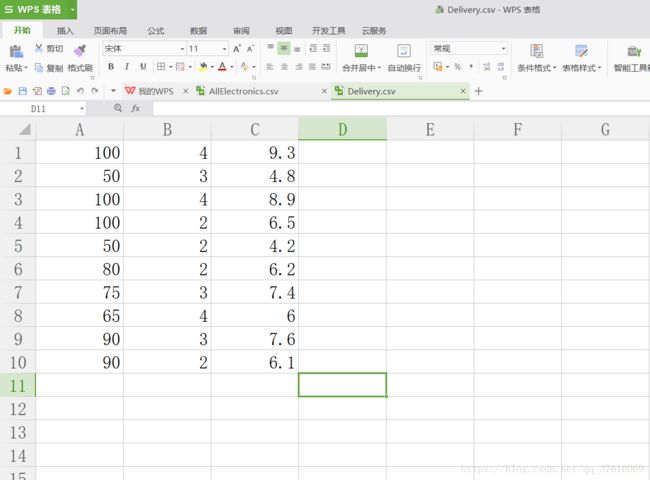
# coding:utf-8 from numpy import genfromtxt import numpy as np from sklearn import datasets, linear_model # 把csv文件转换成矩阵格式 dataPath = r"F:\study\code\python\machine_learning\Regression_problem\Delivery.csv" deliveryData = genfromtxt(dataPath, delimiter=',') print 'data:' print deliveryData # 第一个冒号表示提取所有行,第二个冒号表示提取第一列到倒数第一列但不包括最后一列 X = deliveryData[:, :-1] Y = deliveryData[:, -1] # print "X:", X # print "Y:", Y # 建立模型 regr = linear_model.LinearRegression() regr.fit(X, Y) print "coefficients:" # 平面系数 print regr.coef_ print "intercept:" # 截距或截面 print regr.intercept_ xPredicted = [[102, 6]] yPredicted = regr.predict(xPredicted) print "predicted y:" print yPredicted
delivery.csv:
运行结果:
data:
[[100. 4. 9.3]
[ 50. 3. 4.8]
[100. 4. 8.9]
[100. 2. 6.5]
[ 50. 2. 4.2]
[ 80. 2. 6.2]
[ 75. 3. 7.4]
[ 65. 4. 6. ]
[ 90. 3. 7.6]
[ 90. 2. 6.1]]
coefficients:
[0.0611346 0.92342537]
intercept:
-0.868701466782
predicted y:
[10.90757981]
进程已结束,退出代码0
multiple_Regression_problem(数据集特征值中含有分类值的问题):
解决方法:将某些数据进行特殊处理,即dummy化。
# coding:utf-8 from numpy import genfromtxt import numpy as np from sklearn import datasets, linear_model # 把csv文件转换成矩阵格式 dataPath = r"F:\study\code\python\machine_learning\Regression_problem\Delivery_Dummy.csv" deliveryData = genfromtxt(dataPath, delimiter=',') print 'data:' print deliveryData # 第一个冒号表示提取所有行,第二个冒号表示提取第一列到倒数第一列但不包括最后一列 X = deliveryData[:, :-1] Y = deliveryData[:, -1] # print "X:", X # print "Y:", Y # 建立模型 regr = linear_model.LinearRegression() regr.fit(X, Y) print "coefficients:" # 平面系数 print regr.coef_ print "intercept:" # 截距或截面 print regr.intercept_ xPredicted = [[102, 6, 1, 0, 0]] yPredicted = regr.predict(xPredicted) print "predicted y:" print yPredicted
运行结果:
Delivery_Dummy.csv(已处理好的):C-E列为原数据中的处理结果
data:[[100. 4. 0. 1. 0. 9.3]
[ 50. 3. 1. 0. 0. 4.8]
[100. 4. 0. 1. 0. 8.9]
[100. 2. 0. 0. 1. 6.5]
[ 50. 2. 0. 0. 1. 4.2]
[ 80. 2. 0. 1. 0. 6.2]
[ 75. 3. 0. 1. 0. 7.4]
[ 65. 4. 1. 0. 0. 6. ]
[ 90. 3. 1. 0. 0. 7.6]
[ 90. 2. 0. 0. 1. 6.1]]
coefficients:
[ 0.05520428 0.6952821 -0.16572633 0.58179313 -0.4160668 ]
intercept:
0.209160181582
predicted y:
[9.84596304]
进程已结束,退出代码0
SVM算法:
# coding:utf-8 from sklearn import svm # svm实现太过复杂,现在只谈怎么使用 x = [[1, 1], [2, 0], [2, 3]] # y指的是分类的标记,在python通常用0或者1分类 y = [0, 0, 1] clf = svm.SVC(kernel='linear') clf.fit(x, y) print(clf) # 找出支持向量点 print(clf.support_vectors_) # 找出支持向量点的下标 print(clf.support_) # 分别找出超平面两边各有几个支持向量点 print(clf.n_support_) # 预测 print(clf.predict([[2, .1]]))
运行结果:
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto', kernel='linear',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
[[1. 1.]
[2. 3.]]
[0 2]
[1 1]
[0]
进程已结束,退出代码0
example_1:
# coding:utf-8 # python中支持科学计算的一个包 import numpy as np # python中提供的可以作图的包 import pylab as pl from sklearn import svm # 创建40个点 np.random.seed(0) # 随机生成一个矩阵,通过正态分布的方法随机产生一些数,矩阵有二十行两列,[2, 2]表示均值是2,方差也是2,这样产生的点恰好可以被一条直线分开成两部分 X = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]] # print X # 将这些点进行归类 Y = [0] * 20 + [1] * 20 # print Y # Y = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] # 建立svm模型 clf = svm.SVC(kernel='linear') clf.fit(X, Y) # print clf.support_vectors_ # clf.support_vectors_指的是支持向量点,在本实例中有三个 w = clf.coef_[0] # print w # w = [0.90230696 0.64821811] # 斜率 a = -w[0] / w[1] # print a # 随机生成50个连续的等间隔数列点,-5和5分别表示开头和结尾,可加入第三个参数指定元素个数 xx = np.linspace(-5, 5) # print xx # - (clf.intercept_[0])/w[1]指的是截距 yy = a * xx - (clf.intercept_[0])/w[1] # 找到直线上下方和两个支持向量点相切的直线方程 b = clf.support_vectors_[0] yy_down = a*xx + (b[1] - a*b[0]) b = clf.support_vectors_[-1] yy_up = a*xx + (b[1] - a*b[0]) # 作图 # 三条直线 pl.plot(xx, yy, 'k-') pl.plot(xx, yy_down, 'k--') pl.plot(xx, yy_up, 'k--') # 画点 pl.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=80, facecolors='none') pl.scatter(X[:, 0], X[:, 1], c=Y, cmap=pl.cm.Paired) pl.axis('tight') pl.show()
运行结果:
example_2:
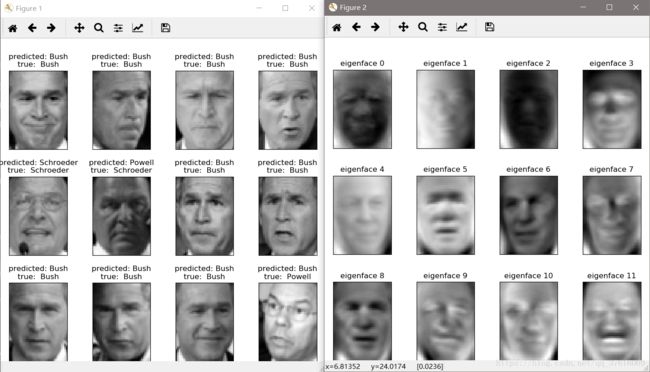
# coding:utf-8 # 用来计时 from time import time # 提供了通用的日志系统 import logging # 将识别的人脸打印出来,这个包提供了绘图的功能 import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split # 用来下载人脸而定数据集 from sklearn.datasets import fetch_lfw_people from sklearn.model_selection import GridSearchCV from sklearn.metrics import classification_report from sklearn.metrics import confusion_matrix from sklearn.decomposition import PCA from sklearn.svm import SVC """ 日志一共分成5个等级,从低到高分别是:DEBUG INFO WARNING ERROR CRITICAL。 DEBUG:详细的信息,通常只出现在诊断问题上 INFO:确认一切按预期运行 WARNING:一个迹象表明,一些意想不到的事情发生了,或表明一些问题在不久的将来(例如。磁盘空间低”)。这个软件还能按预期工作。 ERROR:更严重的问题,软件没能执行一些功能 CRITICAL:一个严重的错误,这表明程序本身可能无法继续运行 logging.basicConfig函数中,可以指定日志的输出格式format,这个参数可以输出很多有用的信息。 %(levelno)s: 打印日志级别的数值 %(levelname)s: 打印日志级别名称 %(pathname)s: 打印当前执行程序的路径,其实就是sys.argv[0] %(filename)s: 打印当前执行程序名 %(funcName)s: 打印日志的当前函数 %(lineno)d: 打印日志的当前行号 %(asctime)s: 打印日志的时间 %(thread)d: 打印线程ID %(threadName)s: 打印线程名称 %(process)d: 打印进程ID %(message)s: 打印日志信息 """ # 把程序进展信息打印出来 logging.basicConfig(level=logging.INFO, format='%(asctime)s %(message)s') # 下载人脸数据集 lfw_people = fetch_lfw_people(min_faces_per_person=70, resize=0.4) # 返回数据集的图片数量以及h,w的值(用于绘图) n_samples, h, w = lfw_people.images.shape # X是特征向量的矩阵,每一行是个实例,每一列是个特征值 X = lfw_people.data # n_features表示的就是维度 # 维度:每个人会提取多少的特征值 n_features = X.shape[1] # 提取每个实例对应每个人脸,目标分类标记,不同的人的身份 y = lfw_people.target target_names = lfw_people.target_names # 多少行,shape就是多少行,多少个人,多少类 n_classes = target_names.shape[0] print("Total dataset size:") # 实例的个数 print("n_samples:%d" % n_samples) # 特征向量的维度 print("n_features:%d" % n_features) # 总共有多少人 print("n_classes:%d" % n_classes) # 下面开始拆分数据,分成训练集和测试集,有个现成的函数,通过调用train_test_split;来分成四部分,即训练集的特征向量,测试集的特征向量,训练集对应的归类标记,测试集对应的归类标记 X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.25) # 数据降维,因为特征值的维度还是比较高 n_components = 150 print("Extracting the top %d eigenfaces from %d faces" % (n_components, X_train.shape[0])) # 记录时间 t0 = time() # 将高维特征向量降低为低维的 pca = PCA(n_components=n_components, whiten=True).fit(X_train) print("done in %0.3fs" % (time() - t0)) # 对于人脸的一张照片上提取的特征值名为eigenfaces eigenfaces = pca.components_.reshape((n_components, h, w)) print("Projecting the inpyt data on the eigenfaces orthonormal basis") t0 = time() # 特征量中训练集所有的特征向量通过pca转换成更低维的矩阵 X_train_pca = pca.transform(X_train) X_test_pca = pca.transform(X_test) print("done in %0.3fs" % (time() - t0)) print "*"*100 # print "X_test_pca",X_test_pca # print "X_train_pca",X_train_pca print("Fitting the classifier to the training set") t0 = time() # param_grid把参数设置成了不同的值,C:权重;gamma:多少的特征点将被使用,因为我们不知道多少特征点最好,选择了不同的组合 param_grid = {'C': [1e3, 5e3, 1e4, 5e4, 1e5], 'gamma': [0.0001, 0.0005, 0.001, 0.005, 0.01, 0.1],} # 把所有我们所列参数的组合都放在SVC里面进行计算,最后看出哪一组函数的表现度最好 clf = GridSearchCV(SVC(kernel='rbf', class_weight='balanced'), param_grid) # 其实建模非常非常简单,主要是数据的预处理麻烦 clf = clf.fit(X_train_pca, y_train) print("done in %0.3fs" % (time() - t0)) print("Best estimator found by grid search:") print(clf.best_estimator_) # 测试集预测看看准确率能到多少 print("Predicting people's names on the test set") t0 = time() y_pred = clf.predict(X_test_pca) print("done in %0.3fs" % (time() - t0)) print(classification_report(y_test, y_pred, target_names=target_names)) print(confusion_matrix(y_test, y_pred, labels=range(n_classes))) # 把数据可视化的可以看到,把需要打印的图打印出来 def plot_gallery(images, titles, h, w, n_row=3, n_col=4): """Helper function to plot a gallery of portraits""" # 在figure上建立一个图当背景 plt.figure(figsize=(1.8*n_col, 2.4*n_row)) plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35) for i in range(n_row * n_col): plt.subplot(n_row, n_col, i+1) plt.imshow(images[i].reshape((h, w)), cmap=plt.cm.gray) plt.title(titles[i], size=12) plt.xticks(()) plt.yticks(()) # 把预测的函数归类标签和实际函数归类标签,比如布什 def title(y_pred, y_test, target_names, i): pred_name = target_names[y_pred[i]].rsplit(' ', 1)[-1] true_name = target_names[y_test[i]].rsplit(' ', 1)[-1] return 'predicted: %s\ntrue: %s'% (pred_name, true_name) # 把预测出来的人名存起来 prediction_titles = [title(y_pred, y_test, target_names, i) for i in range(y_pred.shape[0])] plot_gallery(X_test, prediction_titles, h, w) eigenface_titles = ['eigenface %d' %i for i in range(eigenfaces.shape[0])] # 提取过特征向量之后的脸是什么样子 plot_gallery(eigenfaces, eigenface_titles, h, w) plt.show()
运行结果:
Total dataset size:
n_samples:1288
n_features:1850
n_classes:7
Extracting the top 150 eigenfaces from 966 faces
done in 0.111s
Projecting the inpyt data on the eigenfaces orthonormal basis
done in 0.014s
****************************************************************************************************
Fitting the classifier to the training set
done in 30.601s
Best estimator found by grid search:
SVC(C=1000.0, cache_size=200, class_weight='balanced', coef0=0.0,
decision_function_shape='ovr', degree=3, gamma=0.005, kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
Predicting people's names on the test set
done in 0.079s
precision recall f1-score support
Ariel Sharon 0.92 0.60 0.73 20
Colin Powell 0.81 0.86 0.84 51
Donald Rumsfeld 0.82 0.72 0.77 25
George W Bush 0.80 0.97 0.88 141
Gerhard Schroeder 0.95 0.56 0.71 32
Hugo Chavez 1.00 0.61 0.76 18
Tony Blair 0.94 0.83 0.88 35
avg / total 0.85 0.84 0.83 322
[[ 12 4 0 4 0 0 0]
[ 0 44 0 7 0 0 0]
[ 0 3 18 4 0 0 0]
[ 0 2 2 137 0 0 0]
[ 1 1 1 10 18 0 1]
[ 0 0 0 5 1 11 1]
[ 0 0 1 5 0 0 29]]