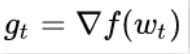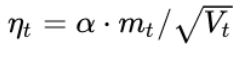常见的损失函数，代价函数以及优化算法汇总
在机器学习和深度学习中，我们通常只需要掌握三个步骤就可以完成训练了，拿起数据（特征），搭上模型（目标函数，损失函数，代价函数）,不断优化（优化函数-梯度下降，adam，动量-找到最优的W），就可以完成了
1. 损失函数、代价函数与目标函数
损失函数（Loss Function）：是定义在单个样本上的，是指一个样本的误差。
代价函数（Cost Function）：是定义在整个训练集上的，是所有样本误差的平均，也就是所有损失函数值的平均。
目标函数（Object Function）：是指最终需要优化的函数，一般来说是经验风险+正则化，也就是（代价函数+正则化项）。
损失函数：
……0-1损失函数
……平方损失函数
……绝对值损失函数
……对数损失函数
……指数损失函数
……铰链损失函数
代价函数：
……均方误差
……均方根误差
……平均绝对误差
……交叉熵代价函数
2. 损失函数
（1）0-1损失函数（0-1 loss function） -----------感知机
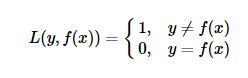
（2）平方损失函数（quadratic loss function）------------线性回归
（3）绝对值损失函数（absolute loss function）
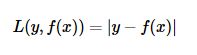
（4）对数损失函数（logarithmic loss function）-----------逻辑回归
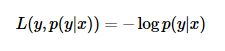
（5）指数损失函数（Exponential Loss Function）----------adaboost
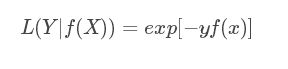
（6）铰链损失函数（Hinge loss） ----------SVM
Hinge loss一般分类算法中的损失函数，尤其是SVM。 其中 y=+1或y=−1，f(x)=wx+b，当为SVM的线性核时。
3. 常用的代价函数
（1）均方误差（Mean Squared Error）-------（平方损失函数）
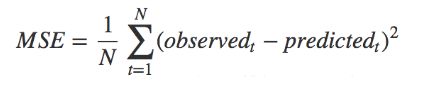
（2）均方根误差-------（平方损失函数）
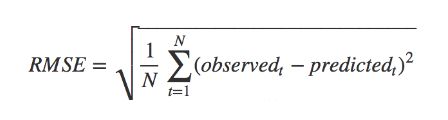
（3）平均绝对误差（Mean Absolute Error）-------（绝对值损失函数）
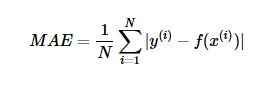
（3）交叉熵代价函数（Cross Entry）----------（对数损失函数）
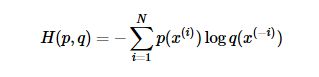
比如对于二分类模型的交叉熵代价函数：
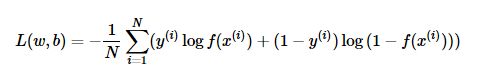
4、经验风险和结构风险
一般来说，目标函数就是代价函数（训练样本的总误差），我们也称代价函数为经验风险
目标函数为经验风险 经验风险=代价函数
结构风险是在经验风险的基础上加上表示模型复杂度的正则项 ----为防止过拟合而提出
目标函数为结构风险 结构风险=经验风险+正则化
5、优化函数
确定了目标函数，接下来的工作就是求最优化的参数W，让目标函数达到最优值
深度学习优化算法经历了 SGD -> SGDM -> NAG ->AdaGrad -> AdaDelta -> Adam -> Nadam
说到优化算法，入门级必从 SGD 学起，SGD没有动量，这是最经典也是目前顶级论文都还在用的算法。
优化算法通用框架
首先定义：待优化参数：w ，目标函数： f(w)，初始学习率 α。而后，开始进行迭代优化。在每个epoch t：
已经确定了目标函数，包含动量
-
计算目标函数关于当前参数的梯度：
-
根据历史梯度计算一阶动量和二阶动量：
-
计算当前时刻的下降梯度：
-
根据下降梯度进行更新：
常见的优化函数：
1、固定学习率的优化算法.
…sgd
…sgd+Momentum
…sgd+Nesterov Acceleration
2、自适应学习率的优化算法
…AdaGrad
…AdaDelta / RMSProp
…Adam
…Nadam
1、固定学习率的优化算法
SGD算法：
梯度下降法的优化思想是用当前位置负梯度方向作为搜索方向，因为该方向为当前位置的最快下降方向
SGD没有动量的概念，也就是说：
计算梯度方向
计算沿着梯度方向下降的距离
更新参数W
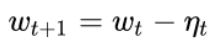
其中，SGD没有用到二阶动量，因此学习率是恒定的（实际使用过程中会采用学习率衰减策略，因此学习率递减）。
SGDM （SGD with Momentum ）算法
为了抑制SGD的震荡，SGDM认为梯度下降过程可以加入惯性。下坡的时候，如果发现是陡坡，那就利用惯性跑的快一些。SGDM全称是SGD with momentum，在SGD基础上引入了一阶动量：
计算梯度方向
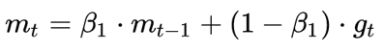
计算沿着梯度方向下降的距离
更新参数W
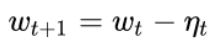
t 时刻的下降方向，不仅由当前点的梯度方向决定，而且由此前累积的下降方向决定（mt-1）。β1的经验值为0.9，这就意味着下降方向主要是此前累积的下降方向，并略微偏向当前时刻的下降方向。
SGD with Nesterov Acceleration
我们知道在时刻 t 的主要下降方向是由累积动量决定的，自己的梯度方向说了也不算，那与其看当前梯度方向，不如先看看如果跟着累积动量走了一步，那个时候再怎么走。因此，NAG在步骤 1，不计算当前位置的梯度方向，而是计算如果按照累积动量走了一步，那个时候的下降方向：
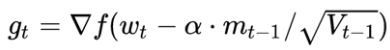
然后用下一个点的梯度方向，与历史累积动量相结合，计算步骤 2 中当前时刻的累积动量。
2、自适应学习率的优化算法
“自适应学习率”优化算法需要用到二阶动量。SGD及其变种以同样的学习率更新每个参数，但深度神经网络往往包含大量的参数，这些参数并不是总会用得到。对于经常更新的参数，我们已经积累了大量关于它的知识，不希望被单个样本影响太大，希望学习速率慢一些；对于偶尔更新的参数，我们了解的信息太少，希望能从每个偶然出现的样本身上多学一些，即学习速率大一些。
AdaGrad
怎么样去度量历史更新频率呢？那就是二阶动量——该维度上，迄今为止所有梯度值的平方和：
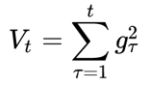
其他按照我们上述的优化算法通用框架计算最优值。
观察我们通用框架中的第三步，此时实质上的学习率由
参数更新越频繁，二阶动量越大，学习率就越小，适合处理稀疏梯度。因为优化算法通用框架中第三步分母是单调递增的，会使得学习率单调递减至0，可能会使得训练过程提前结束，即便后续还有数据也无法学到必要的知识。
AdaDelta / RMSProp
由于AdaGrad单调递减的学习率变化过于激进，我们考虑一个改变二阶动量计算方法的策略：不累积全部历史梯度，而只关注过去一段时间窗口的下降梯度。这也就是AdaDelta名称中Delta的来历。指数移动平均值大约就是过去一段时间的平均值，因此我们用这一方法来计算二阶累积动量：
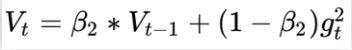
Adam
谈到这里，Adam和Nadam的出现就很自然而然了——它们是前述方法的集大成者。我们看到，SGD-M在SGD基础上增加了一阶动量，AdaGrad和AdaDelta在SGD基础上增加了二阶动量。把一阶动量和二阶动量都用起来，就是Adam了——Adaptive + Momentum。
SGD的一阶动量：
加上AdaDelta的二阶动量：
优化算法里最常见的两个超参数β1，β2就都在这里了，前者控制一阶动量，后者控制二阶动量
Nadam
最后是Nadam。Nadam=Adam+Nesterov
按照NAG的步骤1来计算梯度：
改进地方在第一步加入了Nesterov
另外：
需要注意的是最小二乘法，最小二乘法的解释就是直接求导找出全局最小,是非迭代法。那么在我看来这个最小二乘法既给出了目标函数，同时也给出了优化方式即一步到位。
最小二乘法的目标函数如下，就是平方差的和，为了方便计算通常会在前面乘上1/2：
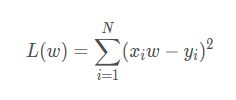
第二步：对目标函数L求导数
第三步：令导数最小或为0，求驻点
参考博客：
https://www.cnblogs.com/adong7639/p/9850379.html
https://www.cnblogs.com/lliuye/p/9549881.html