数据结构第四章树 平衡二叉树,实现插入，删除操作,Java实现,递归实现

二叉搜索树自动调整平衡（左右子树高度差小于等于1）——平衡二叉树

目录

1.编写测试程序，测试二叉树的四种平衡操作

2.编写内部类：树结点

3.根节点，类构造器

4.插入

5.平衡

5.1计算平衡值

5.2.计算深度 

5.3.平衡节点（调用四个旋转的条件）

5.3.1. RR旋转

5.3.2. LL旋转

5.3.3. RL旋转

5.3.4. LR旋转

5.3.5. 逆时针旋转

5.3.6 顺时针旋转

6.删除 

6.1删除无儿子节点

6.2 删除有一个儿子的节点 

6.3 删除有两个儿子的节点 

 7.前序遍历，用于验证二叉树

8.全部代码如下

---

---

1.编写测试程序，测试二叉树的四种平衡操作

public class AVLTree {
	public static void main(String[] args) {
	//验证插入操作
		BalancedBinaryTree test0 = new BalancedBinaryTree(100);	
		test0.insert(50);
		test0.insert(200);
		System.out.print("草稿纸上运算为{100,50,200}: ");
		test0.preOrder();
		System.out.println();
		
	//验证LL旋转
		//发生在root
		BalancedBinaryTree test1 = new BalancedBinaryTree(100);	
		test1.insert(70);
		test1.insert(30);
		test1.insert(10);
		test1.insert(5);
		System.out.print("草稿纸上运算为{70,10,5,30,100}: ");
		test1.preOrder();
		System.out.println();
		//发生在非root
		BalancedBinaryTree test4 = new BalancedBinaryTree(100);	
		test4.insert(50);
		test4.insert(200);
		test4.insert(150);
		test4.insert(130);
		System.out.print("草稿纸上运算为{100,50,150,130,200 }: ");
		test4.preOrder();
		System.out.println();	
		
	//验证RR旋转
		//发生在root
		BalancedBinaryTree test2 = new BalancedBinaryTree(100);	
		test2.insert(200);
		test2.insert(300);
		test2.insert(400);
		test2.insert(500);
		System.out.print("草稿纸上运算为{200,100,400,300,500}: ");
		test2.preOrder();
		System.out.println();
		//发生在非root
		BalancedBinaryTree test3 = new BalancedBinaryTree(100);	
		test3.insert(50);
		test3.insert(200);
		test3.insert(75);
		test3.insert(80);
		System.out.print("草稿纸上运算为{100,75,50,80,200}: ");
		test3.preOrder();
		System.out.println();
		
	//验证LR旋转
		BalancedBinaryTree test5 = new BalancedBinaryTree(100);	
		test5.insert(50);
		test5.insert(200);
		test5.insert(75);
		test5.insert(30);
		test5.insert(80);
		System.out.print("LR草稿纸上运算为{75,50,30,100,80,200}: ");
		test5.preOrder();
		System.out.println();
		
	//验证RL旋转
		BalancedBinaryTree test6 = new BalancedBinaryTree(100);	
		test6.insert(50);
		test6.insert(200);
		test6.insert(150);
		test6.insert(300);
		test6.insert(125);
		System.out.print("RL草稿纸上运算为{150,100,50,125,200,300}: ");
		test6.preOrder();
		System.out.println();	
	
	
	//验证删除操作
		BalancedBinaryTree test7 = new BalancedBinaryTree(100);	
		test7.insert(50);
		test7.insert(200);
		test7.insert(150);
		test7.insert(300);
		test7.insert(25);
		test7.insert(75);
		System.out.print("delete草稿纸上运算为{100,50,25,75,200,150,300}: ");
		test7.preOrder();
		System.out.println();
		
		//删除没有儿子的节点
		test7.delete(150);
		System.out.print("删除没有儿子的节点150，delete草稿纸上运算为{100 50 25 75 200 300 }: ");
		test7.preOrder();
		System.out.println();
		//删除有一个儿子的节点
		test7.delete(200);
		System.out.print("删除有一个儿子的节点200，delete草稿纸上运算为{100 50 25 75 200 300 }: ");
		test7.preOrder();
		System.out.println();
		//删除有两个儿子的节点
		test7.delete(100);
		System.out.print("删除有两个儿子的节点100，delete草稿纸上运算为{75,50,25,300}: ");
		test7.preOrder();
		System.out.println();
		
		test7.delete(75);
		System.out.print("删除节点75，delete草稿纸上运算为{50,25,300}: ");
		test7.preOrder();
		System.out.println();
		
		test7.delete(50);
		System.out.print("删除节点50，delete草稿纸上运算为{25,300}: ");
		test7.preOrder();
		System.out.println();
	}
}

2.编写内部类：树结点

        class AVLNode {
		public int data;
		public int depth;//当前子树深度的 depth
		public int balance;
		public AVLNode parent = null;//指向父节点的指针
		public AVLNode left = null;
		public AVLNode right = null;
		
		public AVLNode() {
			depth = 1;
			balance = 0;
			left = null;
			right = null;
		}
		
		public AVLNode(int data) {
			this.data = data;
			depth = 1;
			balance = 0;
			left = null;
			right = null;			
		}
	}

3.根节点，类构造器

class BalancedBinaryTree {
	/**
	 *  根节点
	 */
	private AVLNode root = null;
    /**
	 * 构造器
	 */
	public BalancedBinaryTree()	{		
	}
	
	public BalancedBinaryTree(int data)	{
		root = new AVLNode(data);
	}
    //以及别的操作
}

4.插入

插入过程分为：二叉查找树的插入过程+再平衡过程

再平衡过程分为：计算深度和平衡值+进行平衡操作

        public void insert(int data) {
		if (root == null) {
			root = new AVLNode(data);
		} else {
			insertSon(root, data);
		}
	}
	
	private void insertSon(AVLNode node, int data) {
		if (data < node.data) {
			if (node.left != null) {
				insertSon(node.left, data);
			} else {
				node.left = new AVLNode(data);
				node.left.parent = node;//子节点锁住parent
			}
		} else {
			if (node.right != null) {
				insertSon(node.right, data);
			} else {
				node.right = new AVLNode(data);
				node.right.parent = node;
			}
		}
		// 计算平衡和深度
		node.balance = calculateBalance(node);
		node.depth = calculateDepth(node);
		// 平衡节点
		balanceNode(node);
	}

5.平衡

5.1计算平衡值

        private int calculateBalance(AVLNode node) {
		int leftDepth;
		int rightDepth;
		if (node.left != null) {
			leftDepth = node.left.depth;
		} else {
			leftDepth = 0;
		}
		if (node.right != null) {
			rightDepth = node.right.depth;
		} else {
			rightDepth = 0;
		}
		return leftDepth - rightDepth;
	}

5.2.计算深度 

	private int calculateDepth(AVLNode node) {
		int depth = 0;
		if (node.left != null) {
			depth = node.left.depth;
		}
		if (node.right != null && depth < node.right.depth) {
			depth = node.right.depth;
		}
		depth++;
		return depth;
	}

5.3.平衡节点（调用四个旋转的条件）

根据balance的数值，找出不平衡的地方进行调整操作（RR，RL，LR，LL）

        private void balanceNode(AVLNode node) {
		if (node.balance <= -2) {
			if (node.right.balance == -1) {
				// RR插入，RR旋转
				rightRightRotate(node);
			} else {
				// RL插入，RL旋转
				rightLeftRotate(node);
			}
		} else if (node.balance >= 2) {
			if (node.left.balance == 1) {
				// LL插入，LL旋转
				leftLeftRotate(node);
			} else {
				// LR插入，LR旋转
				leftRightRotate(node);
			}
		}
	}

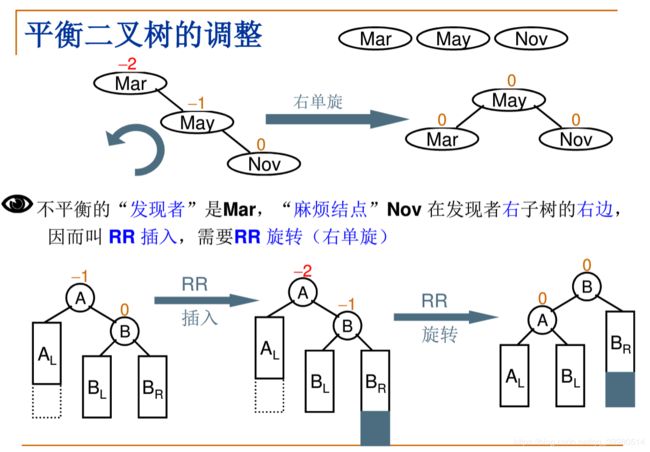
5.3.1. RR旋转

如图A，B节点进行逆时针旋转

图片来源：中国MOOC浙大数据结构第四章

    public void rightRightRotate(AVLNode node) {
        counterClockwiseRotate(node);
    }

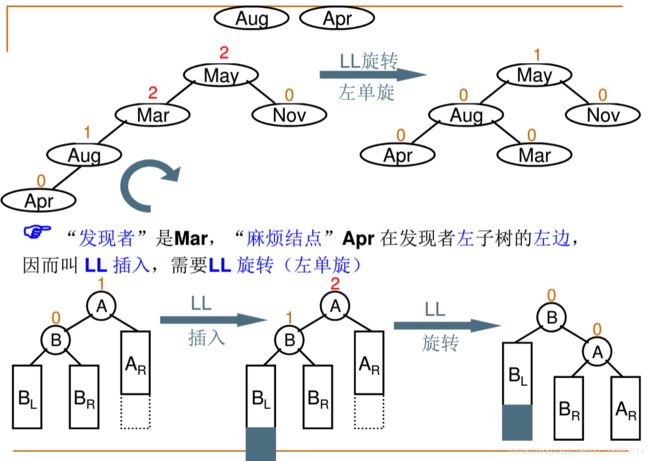
5.3.2. LL旋转

如图A，B两个节点进行顺时针旋转

图片来源：中国MOOC浙大数据结构第四章

 

        public void leftLeftRotate(AVLNode node) {
		clockwiseRotate(node);
	}

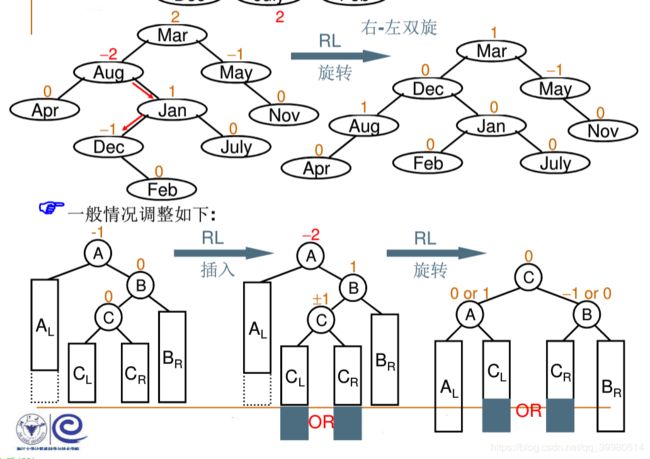
5.3.3. RL旋转

先对C，B两个节点先进行逆时针旋转，再对A，C两个节点顺时针旋转

图片来源：中国MOOC浙大数据结构第四章

 

        public void rightLeftRotate(AVLNode node) {
		clockwiseRotate(node.right);
		counterClockwiseRotate(node);
	}

 

5.3.4. LR旋转

先B，C逆时针旋转，再A，B顺时针旋转

图片来源：中国MOOC浙大数据结构第四章

        public void leftRightRotate(AVLNode node) {
		counterClockwiseRotate(node.left);
		clockwiseRotate(node);
	}

5.3.5. 逆时针旋转

重新用回RR旋转的图，逆时针旋转就是一个RR旋转，本质就是交换A，B节点对别的节点的引用，再交换别的节点对A，B节点的引用而已。

        public void counterClockwiseRotate(AVLNode node) {
		AVLNode nodeOriginRight = node.right;
	//1.右子树占node位
		if(node.parent == null) { // 先确定是不是根节点，根节点不用处理parent
		
			nodeOriginRight.parent = null;
			root = nodeOriginRight;
		} else {
			if(node.parent.left.equals(node)) {
				node.parent.left = nodeOriginRight;
			} else {
				node.parent.right = nodeOriginRight;
			}
			nodeOriginRight.parent = node.parent;
		}
		 
	//2.node变成原右子树的左子树
		AVLNode bl = nodeOriginRight.left; 
		nodeOriginRight.left = node;
		node.parent = nodeOriginRight;
		
	//3.node新右子树变为原右子树的的左子树
		node.right = bl;
		if (bl != null) { // 有可能bl是null
			bl.parent = node;
		}
		node.balance = calculateBalance(node);
		node.depth = calculateDepth(node);
		nodeOriginRight.balance = calculateBalance(nodeOriginRight);
		nodeOriginRight.depth = calculateDepth(nodeOriginRight);
	}

5.3.6 顺时针旋转

就是逆时针操作反过来而已

        public void clockwiseRotate(AVLNode node) { 
		AVLNode nodeOriginLeft = node.left;
	// 1.左子树占node位
		if (node.parent == null) {
			nodeOriginLeft.parent = null;
			root = nodeOriginLeft;
		} else { // 更改node父节点的指向子结点指针
			if(node.parent.left.equals(node)) {
				node.parent.left = nodeOriginLeft;
			} else {
				node.parent.right = nodeOriginLeft;
			}
			nodeOriginLeft.parent = node.parent;
		} 
	//2.node变成原左子树的右子树
		AVLNode br = nodeOriginLeft.right; 
		nodeOriginLeft.right = node;
		node.parent = nodeOriginLeft;
		
	//3.node新左子树变为原左子树的的右子树
		node.left = br;
		if (br != null) {
			br.parent = node;
		}
		node.balance = calculateBalance(node);
		node.depth = calculateDepth(node);
		nodeOriginLeft.balance = calculateBalance(nodeOriginLeft);
		nodeOriginLeft.depth = calculateDepth(nodeOriginLeft);
	}

6.删除 

删除有三种情况，删除节点没有儿子，删除节点有一个儿子，删除节点有两个儿子。

步骤为：先比较大小确定是否是要删除节点，再根据有几个儿子调用不同的删除方法，删除完后进行平衡

        public void delete(int data) {
		if (root != null) {
			deleteDetail(root, data);
		}
	}
	
	private void deleteDetail(AVLNode node, int data) {
		if (data < node.data) {
			if (node.left != null) {
				deleteDetail(node.left, data);
			}
		} else if (data > node.data) {
			if(node.right != null) {
				deleteDetail(node.right, data);
			}
		} else { // 不大不小则是节点是要删除节点
			if (node.left == null && node.right == null) { // 没有儿子
				deleteSonWithNoChild(node);
			} else if (node.left == null || node.right == null) { // 有一个儿子
				deleteSonWithOneChild(node);			
			} else { // 有两个儿子
				deleteSonWithTwoChild(node);
			}
		}
		// 计算平衡和深度
		// 由于node已被替换，且替换node的节点已经平衡过或不需要平衡，为了整个递归的平衡过程，这里平衡node的父节点
		if (node.parent != null) {
			node.parent.balance = calculateBalance(node.parent);
			node.parent.depth = calculateDepth(node.parent);
			// 平衡节点
			balanceNode(node.parent);
		}
	}

6.1删除无儿子节点

父节点的引用改为null即可

        private void deleteSonWithNoChild(AVLNode node) {
		if (node.parent == null) {
			root = null;
		} else if (node.parent.left == node) {
			node.parent.left = null;
		} else if (node.parent.right == node) {
			node.parent.right = null;
		}
	}

6.2 删除有一个儿子的节点 

父节点的儿子引用指向孙子节点，孙子节点的父引用指向父节点

        private void deleteSonWithOneChild(AVLNode node) {
		AVLNode temporary = ((node.right == null) ? node.left : node.right);
		if (node.parent == null) {
			root = temporary;
		} else if (node.parent.left == node) {
			node.parent.left = temporary;
		} else if (node.parent.right == node) {
			node.parent.right = temporary;
		}
		temporary.parent = node.parent;
	}

6.3 删除有两个儿子的节点 

用左子树的最大节点（也可以用右子树最小节点）来替换被删除节点，步骤为：

1.保存左子最大树节点数据

2.删除左子最大树节点（这个节点要么没儿子，要么只有一个儿子）

3.将要被删除节点数据替换为左子最大树节点数据（由于步骤2删除过程已调过平衡，这个节点不用再调平衡）

        private void deleteSonWithTwoChild(AVLNode node) {
		AVLNode temporary = searchMax(node.left);// 左子树最大的的节点可以替换删除的node
		delete(temporary.data);
		node.data = temporary.data;// 直接换数据
	}

	private AVLNode searchMax(AVLNode node) {
		if (node.right == null) {
			return node;
		} else {
			return searchMax(node.right);
		}
	}

 7.前序遍历，用于验证二叉树

        public void preOrder() {
		if (root != null) {
			 preOrderDetail(root);
		}
	}
	public void preOrderDetail(AVLNode node) {
		if (node != null) {
			System.out.print(node.data);
			System.out.print(" ");
			preOrderDetail(node.left);
			preOrderDetail(node.right);
		}
	}

8.全部代码如下

package BinaryTree;
public class AVLTree {
	public static void main(String[] args) {
	// 验证插入操作
		BalancedBinaryTree test0 = new BalancedBinaryTree(100);	
		test0.insert(50);
		test0.insert(200);
		System.out.print("草稿纸上运算为{100,50,200}: ");
		test0.preOrder();
		System.out.println();
		
	// 验证LL旋转
		// 发生在root
		BalancedBinaryTree test1 = new BalancedBinaryTree(100);	
		test1.insert(70);
		test1.insert(30);
		test1.insert(10);
		test1.insert(5);
		System.out.print("草稿纸上运算为{70,10,5,30,100}: ");
		test1.preOrder();
		System.out.println();
		// 发生在非root
		BalancedBinaryTree test4 = new BalancedBinaryTree(100);	
		test4.insert(50);
		test4.insert(200);
		test4.insert(150);
		test4.insert(130);
		System.out.print("草稿纸上运算为{100,50,150,130,200 }: ");
		test4.preOrder();
		System.out.println();	
		
	// 验证RR旋转
		// 发生在root
		BalancedBinaryTree test2 = new BalancedBinaryTree(100);	
		test2.insert(200);
		test2.insert(300);
		test2.insert(400);
		test2.insert(500);
		System.out.print("草稿纸上运算为{200,100,400,300,500}: ");
		test2.preOrder();
		System.out.println();
		// 发生在非root
		BalancedBinaryTree test3 = new BalancedBinaryTree(100);	
		test3.insert(50);
		test3.insert(200);
		test3.insert(75);
		test3.insert(80);
		System.out.print("草稿纸上运算为{100,75,50,80,200}: ");
		test3.preOrder();
		System.out.println();
		
	// 验证LR旋转
		BalancedBinaryTree test5 = new BalancedBinaryTree(100);	
		test5.insert(50);
		test5.insert(200);
		test5.insert(75);
		test5.insert(30);
		test5.insert(80);
		System.out.print("LR草稿纸上运算为{75,50,30,100,80,200}: ");
		test5.preOrder();
		System.out.println();
		
	// 验证RL旋转
		BalancedBinaryTree test6 = new BalancedBinaryTree(100);	
		test6.insert(50);
		test6.insert(200);
		test6.insert(150);
		test6.insert(300);
		test6.insert(125);
		System.out.print("RL草稿纸上运算为{150,100,50,125,200,300}: ");
		test6.preOrder();
		System.out.println();	
	
	
	// 验证删除操作
		BalancedBinaryTree test7 = new BalancedBinaryTree(100);	
		test7.insert(50);
		test7.insert(200);
		test7.insert(150);
		test7.insert(300);
		test7.insert(25);
		test7.insert(75);
		System.out.print("delete草稿纸上运算为{100,50,25,75,200,150,300}: ");
		test7.preOrder();
		System.out.println();
		
		// 删除没有儿子的节点
		test7.delete(150);
		System.out.print("删除没有儿子的节点150，delete草稿纸上运算为{100 50 25 75 200 300 }: ");
		test7.preOrder();
		System.out.println();
		// 删除有一个儿子的节点
		test7.delete(200);
		System.out.print("删除有一个儿子的节点200，delete草稿纸上运算为{100 50 25 75 200 300 }: ");
		test7.preOrder();
		System.out.println();
		// 删除有两个儿子的节点
		test7.delete(100);
		System.out.print("删除有两个儿子的节点100，delete草稿纸上运算为{75,50,25,300}: ");
		test7.preOrder();
		System.out.println();
		
		test7.delete(75);
		System.out.print("删除有两个儿子的节点75，delete草稿纸上运算为{50,25,300}: ");
		test7.preOrder();
		System.out.println();
		
		test7.delete(50);
		System.out.print("删除有两个儿子的节点50，delete草稿纸上运算为{25,300}: ");
		test7.preOrder();
		System.out.println();
	}
}

class BalancedBinaryTree {// 本类对插入相同数值，删除不存在数值的行为不会有反应
	/**
	 *  节点
	 */
	class AVLNode {
		public int data;
		public int depth;
		public int balance;
		public AVLNode parent = null;
		public AVLNode left = null;
		public AVLNode right = null;
		
		public AVLNode() {
			depth = 1;
			balance = 0;
			left = null;
			right = null;
		}
		
		public AVLNode(int data) {
			this.data = data;
			depth = 1;
			balance = 0;
			left = null;
			right = null;			
		}
	}
	
	/**
	 * 根节点
	 */
	private AVLNode root = null;
	/**
	 * 构造器
	 */
	public BalancedBinaryTree() {
	}
	
	public BalancedBinaryTree(int data) {
		root = new AVLNode(data);
	}
	
	/**
	 *  插入
	 */
	public void insert(int data) {
		if (root == null) {
			root = new AVLNode(data);
		} else {
			insertSon(root, data);
		}
	}
	
	private void insertSon(AVLNode node, int data) {
		if (data < node.data) {
			if (node.left != null) {
				insertSon(node.left, data);
			} else {
				node.left = new AVLNode(data);
				node.left.parent = node;//子节点锁住parent
			}
		} else {
			if (node.right != null) {
				insertSon(node.right, data);
			} else {
				node.right = new AVLNode(data);
				node.right.parent = node;
			}
		}
		// 计算平衡和深度
		node.balance = calculateBalance(node);
		node.depth = calculateDepth(node);
		// 平衡节点
		balanceNode(node);
	}
	
	/**
	 * 删除
	 */
	public void delete(int data) {
		if (root != null) {
			deleteDetail(root, data);
		}
	}
	
	private void deleteDetail(AVLNode node, int data) {
		if (data < node.data) {
			if (node.left != null) {
				deleteDetail(node.left, data);
			}
		} else if (data > node.data) {
			if(node.right != null) {
				deleteDetail(node.right, data);
			}
		} else { // 不大不小则是节点是要删除节点
			if (node.left == null && node.right == null) { // 没有儿子
				deleteSonWithNoChild(node);
			} else if (node.left == null || node.right == null) { // 有一个儿子
				deleteSonWithOneChild(node);			
			} else { // 有两个儿子
				deleteSonWithTwoChild(node);
			}
		}
		// 计算平衡和深度
		// 由于node已被替换，且替换node的节点已经平衡过或不需要平衡，为了整个递归的平衡过程，这里平衡node的父节点
		if (node.parent != null) {
			node.parent.balance = calculateBalance(node.parent);
			node.parent.depth = calculateDepth(node.parent);
			// 平衡节点
			balanceNode(node.parent);
		}
	}
	
	private void deleteSonWithNoChild(AVLNode node) {
		if (node.parent == null) {
			root = null;
		} else if (node.parent.left == node) {
			node.parent.left = null;
		} else if (node.parent.right == node) {
			node.parent.right = null;
		}
	}
	
	private void deleteSonWithOneChild(AVLNode node) {
		AVLNode temporary = ((node.right == null) ? node.left : node.right);
		if (node.parent == null) {
			root = temporary;
		} else if (node.parent.left == node) {
			node.parent.left = temporary;
		} else if (node.parent.right == node) {
			node.parent.right = temporary;
		}
		temporary.parent = node.parent;
	}
	
	private void deleteSonWithTwoChild(AVLNode node) {
		AVLNode temporary = searchMax(node.left);// 左子树最大的的节点可以替换删除的node
		delete(temporary.data);
		node.data = temporary.data;// 直接换数据
	}

	private AVLNode searchMax(AVLNode node) {
		if (node.right == null) {
			return node;
		} else {
			return searchMax(node.right);
		}
	}
	/**
	 * 计算平衡值
	 */
	private int calculateBalance(AVLNode node) {
		int leftDepth;
		int rightDepth;
		if (node.left != null) {
			leftDepth = node.left.depth;
		} else {
			leftDepth = 0;
		}
		if (node.right != null) {
			rightDepth = node.right.depth;
		} else {
			rightDepth = 0;
		}
		return leftDepth - rightDepth;
	}
	
	/**
	 * 计算深度
	 */
	private int calculateDepth(AVLNode node) {
		int depth = 0;
		if (node.left != null) {
			depth = node.left.depth;
		}
		if (node.right != null && depth < node.right.depth) {
			depth = node.right.depth;
		}
		depth++;
		return depth;
	}
	
	/**
	 * 平衡
	 */
	private void balanceNode(AVLNode node) {
		if (node.balance <= -2) {
			if (node.right.balance == -1) {
				// RR插入，RR旋转
				rightRightRotate(node);
			} else {
				// RL插入，RL旋转
				rightLeftRotate(node);
			}
		} else if (node.balance >= 2) {
			if (node.left.balance == 1) {
				// LL插入，LL旋转
				leftLeftRotate(node);
			} else {
				// LR插入，LR旋转
				leftRightRotate(node);
			}
		}
	}
	
	/**
	 * 旋转
	 */
	// 四种旋转
	public void rightRightRotate(AVLNode node) {
		counterClockwiseRotate(node);
	}
	
	public void rightLeftRotate(AVLNode node) {
		clockwiseRotate(node.right);
		counterClockwiseRotate(node);
	}
	
	public void leftRightRotate(AVLNode node) {
		counterClockwiseRotate(node.left);
		clockwiseRotate(node);
	}
	
	public void leftLeftRotate(AVLNode node) {
		clockwiseRotate(node);
	}
	
	// 两个基本旋转
	// 逆时针旋转
	public void counterClockwiseRotate(AVLNode node) {
		AVLNode nodeOriginRight = node.right;
	//1.右子树占node位
		if(node.parent == null) { // 先确定是不是根节点，根节点不用处理parent
		
			nodeOriginRight.parent = null;
			root = nodeOriginRight;
		} else {
			if(node.parent.left.equals(node)) {
				node.parent.left = nodeOriginRight;
			} else {
				node.parent.right = nodeOriginRight;
			}
			nodeOriginRight.parent = node.parent;
		}
		 
	//2.node变成原右子树的左子树
		AVLNode bl = nodeOriginRight.left; 
		nodeOriginRight.left = node;
		node.parent = nodeOriginRight;
		
	//3.node新右子树变为原右子树的的左子树
		node.right = bl;
		if (bl != null) { // 有可能bl是null
			bl.parent = node;
		}
		node.balance = calculateBalance(node);
		node.depth = calculateDepth(node);
		nodeOriginRight.balance = calculateBalance(nodeOriginRight);
		nodeOriginRight.depth = calculateDepth(nodeOriginRight);
	}
	// 顺时针旋转：counterClockwiseRotate代码反过来
	public void clockwiseRotate(AVLNode node) { 
		AVLNode nodeOriginLeft = node.left;
	// 1.左子树占node位
		if (node.parent == null) {
			nodeOriginLeft.parent = null;
			root = nodeOriginLeft;
		} else { // 更改node父节点的指向子结点指针
			if(node.parent.left.equals(node)) {
				node.parent.left = nodeOriginLeft;
			} else {
				node.parent.right = nodeOriginLeft;
			}
			nodeOriginLeft.parent = node.parent;
		} 
	//2.node变成原左子树的右子树
		AVLNode br = nodeOriginLeft.right; 
		nodeOriginLeft.right = node;
		node.parent = nodeOriginLeft;
		
	//3.node新左子树变为原左子树的的右子树
		node.left = br;
		if (br != null) {
			br.parent = node;
		}
		node.balance = calculateBalance(node);
		node.depth = calculateDepth(node);
		nodeOriginLeft.balance = calculateBalance(nodeOriginLeft);
		nodeOriginLeft.depth = calculateDepth(nodeOriginLeft);
	}
	
	/**
	 * 前序遍历
	 */
	public void preOrder() {
		if (root != null) {
			 preOrderDetail(root);
		}
	}
	public void preOrderDetail(AVLNode node) {
		if (node != null) {
			System.out.print(node.data);
			System.out.print(" ");
			preOrderDetail(node.left);
			preOrderDetail(node.right);
		}
	}	
}