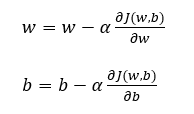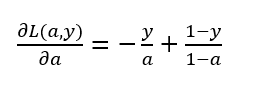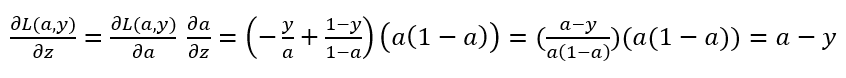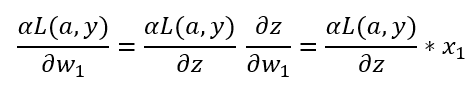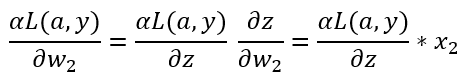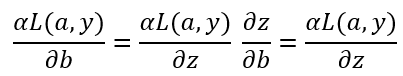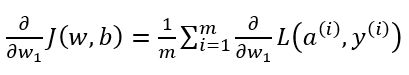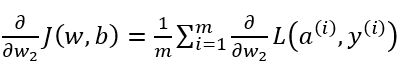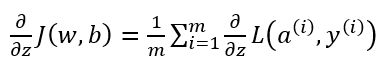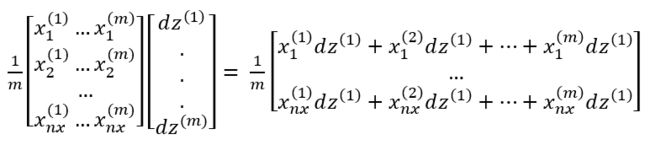二元分类(Binary Classfication)与logistic回归

目录

 

二元分类

Logistic回归

成本函数

梯度下降

logistic回归中的梯度下降

向量化

python代码

---

二元分类

二元分类是监督学习中分类问题的基本应用。监督学习通俗来讲就是训练集拥有正确的标签，例如你想根据房子的尺寸、卧室数等特征预测房价，那么你的训练集中除了有房子的特征以外，还得有这些房子的实际交易价格。与监督学习相对的是无监督学习，无监督学习中的训练集没有正确的标签，就好像你扔给了计算机一大堆数据，让计算机自己去学着找出里面有用的信息。监督学习中主要分为二类模型，回归和分类。生活中有许多二元分类的应用，例如你收到一封邮件，你想判断它是否是垃圾邮件？或者在银行的业务中，银行需要判断是否贷款给某个客户？

下面给出一个二元分类中的图像识别问题的例子

 

假设你有一张图片作为输入，你想识别这张图是否为猫？如果是猫，输出1，否则，输出0，输出结果用y来表示。

那么首先需要知道图片在计算机中是如何表示的？

图像在计算机中以像素为基本单位存储为数据矩阵，最简单的图像就是单通道的灰度图，在灰度图中每个位置(x,y)对应一个灰度值

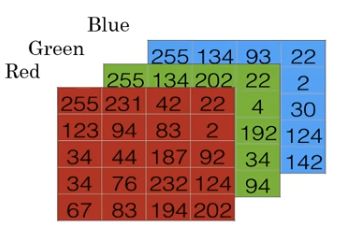
如果是彩色RGB图像，那么计算机需要保存三个独立矩阵，分别对应图片在红、绿、蓝三个颜色通道的像素。如果输入的图片是64x64像素的，那就有3个64x64的矩阵，分别对应图片中红、绿、蓝三种像素的强度。

将所有的像素值取出来放入特征向量x以表示这张图片，上图中转换的方法是x为(255,131...194 202 然后是绿色通道 255 134 ...94, 最后是蓝色通道 255 134... 142)，如果图片是64x64的，那么向量x的总维度就是64x64x3，即12288。用来表示输入的特征向量x的维度。

在这个二元分类问题中，目标是训练一个分类器。分类器以特征向量x作为输入，然后输出这张图片是1还是0(即是否是猫)。

下面先进行一些符号说明：

---

(x,y)表示一个训练样本，x是维的特征向量，y是标签(0或1)。

m表示训练集中训练样本的个数，表示第一个训练样本。

矩阵表示维度为 x m的矩阵，这个矩阵代表所有训练样本的特征向量x，每一列代表一个训练样本的特征向量。

矩阵表示维度为1 x m的矩阵，这个矩阵代表所有训练样本的标签，每一列代表一个训练样本的标签。

---

Logistic回归

为了解决二元分类问题，下面将介绍logistic回归，它通常用于监督学习问题的输出标签是0或1时，即一个二元分类问题时。

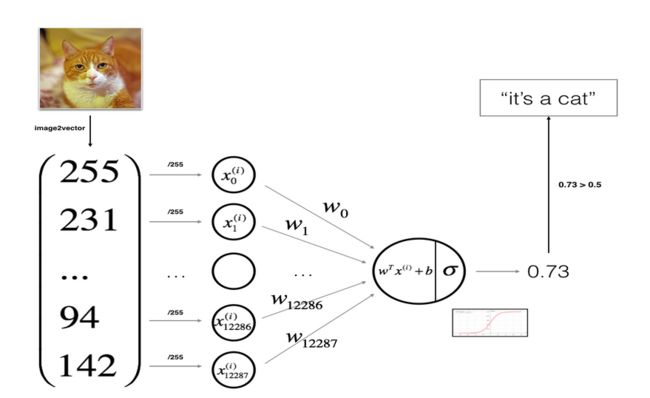
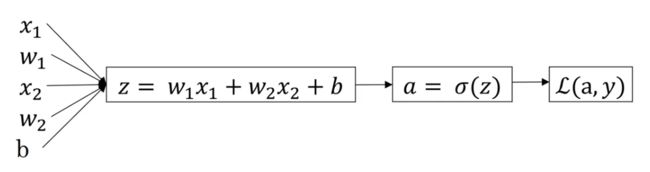
下图是logistic回归算法的结构图示例，其中除以255是数据预处理步骤，这只是为了集中和标准化我们的训练集。

Logistic回归其实是一个很小的神经网络，对于每一张照片我们将它当作输入向量x，然后我们需要给出预测值a，即我们需要找到一种很好的关系来使得我们的预测值尽可能接近实际的标签。而Logistic回归需要不断通过正向传播和反向传播来学习参数(即学习到一种关系)。从输入x到给出预测值的过程称为正向传播，而通过得到的预测值从后往前对w和b进行求导叫做反向传播过程。

对于一张图片，将它转换为特征向量x输入算法后，我们期望算法告诉我们这张图是否是一只猫，算法通常会给出一个预测值a，a通常是一个概率值，表示这张图片为正类(即为1)的概率，为了决定这个预测的结果是正类还是负类，我们通常还需要设定一个阈值，任何大于这个阈值的都为正类，否则，为负类。

设logistic回归的参数是w，它的维度等于输入特征向量的维度，即w是一个维的向量，而b是一个实数。

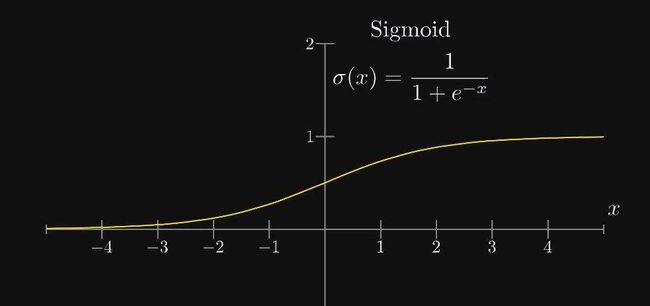
那么已知输入x和参数w，b，我们如何计算预测值a呢？ 如果我们计算a=，即w是x的线性函数。事实上，如果你这么做的话，你其实是在用线性回归算法，线性回归算法并不是一个好的二元分类算法。在此，给出一个不正式的证明，直观上来说，你期望算法的输出a是一个概率，它表示这张图是1的概率，所以a应该是位于0~1之间的，但实际上可能是负值，也可能是比1大得多的值，这并不符合我们的要求。所以我们可以对线性回归的值再用一层激活函数，让，σ函数的图形如下所示：

直观上可以看到σ函数的值域是0~1，因此这也使得我们的预测值a永远在(0,1)之间。

在logistic回归中，我们需要做的就是根据训练集来训练得到参数w和b的值使得我们的预测输出a尽可能接近真实标签值y。这样，在给出一张新的图片时，我们可以根据参数w和b计算得到a，从而预测出这张新的图片是否是一只猫？

成本函数

为了训练logistic回归的参数w和b，需要定义一个成本函数。

在定义成本函数之前，我们需要先定义损失函数(Loss function)，损失函数衡量的是单个样本的预测值和实际标签值之间的误差。

为了衡量误差，可以定义损失函数为我们熟悉的误差平方函数 ，结果表明可以这么做，但在logistic回归中，大家通常不这样做。因为使用平方差函数会使得后面的优化问题变成非凸的(这里不做证明)，直观上这会使得我们最后得到很多个局部最优解，这就使得诸如梯度下降法之类的优化算法找不到全局最优值。误差平方函数看起来是一个不错的选择，但用这个函数的话，会使得优化算法不太好用。

在logistic回归中，定义的损失函数为 ，这里的log表示以自然数e为底，它起着与平方误差函数相似的作用，并且会使问题变为凸优化问题，这会让我们得到全局最优值，而不会陷入局部最优的问题。

直观上来理解这个损失函数为什么能起作用？首先，我们希望误差函数越小越好，因为这表明我们的预测很准确。

当y=1时，因为第二项为0 ，所以损失函数变为，所以我们希望尽可能小，所以就要尽可能大，即a要尽可能大，但是a是由σ函数所得，即a最大不超过1，也就是说，当实际标签y=1时，我们希望预测值a也尽可能接近1，这符合我们的要求。

如果y=0，第一项变为0，所以损失函数为，我们希望尽可能小，即尽可能大，所以这使得a尽可能小，a最小不超过0，所以，实际标签为0时，我们希望预测值a尽可能接近0。

下面来看成本函数，损失函数衡量的是单个样本的表现，而成本函数衡量的是全体训练样本的表现，下面是成本函数的定义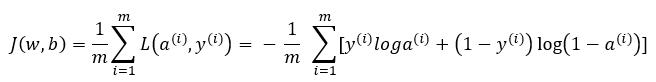

梯度下降

为了根据训练集学习得到参数w和b，我们需要使用优化算法，梯度下降法就是优化算法中的一种。很容易想到，我们最终得到的w和b一定是可以让成本函数J(w,b)尽可能小的。

上图是成本函数关于参数w，b的曲面图，在实践中，w可以是更高维的，但这里为了方便绘图，w和b都是实数，曲面的高度代表J(w,b)在某一点的值。梯度下降法要做的是，找到某一点，使得J(w,b)的函数值最小，可以看到这个成本函数呈现碗状，这其实是一个凸函数，它只有一个全局最优值。凸函数这个性质是logistic回归使用上述成本函数J的一个重要原因。

我们要做的就是随机任意初始化w和b，然后不断用下面的式子更新w和b的值。其中，α表示学习率，它控制更新的速率。

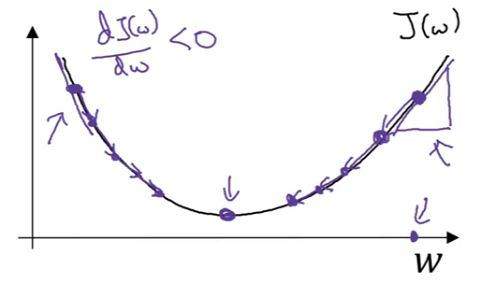
为了更直观地说明这个更新式子在做什么，先假设没有b参数，只有w参数，然后绘制J(w)关于w的参数一个函数图像

导数通俗来讲就是斜率，假设初始化W在右边，因为导数是正的，那么更新式子会使得J(w)不断向左移动，直到最低点。如果是在左边初始化，由于导数是负的，J(w)会不断向右移动，直到最低点。

logistic回归中的梯度下降

为了求得使得J(w,b)最小的w和b的值，那么就需要求得J(w,b)对w和b的导数。为了便于理解，先从单个训练样本的损失函数推导导数的计算。

首先我们从最后面向前一步计算，即计算损失函数L对a的导数

然后再向前计算一步

接着再向前计算

以上就是单个样本实例的一次梯度更新步骤，如果你对链式求导比较熟悉，可以自己验证上面的式子是否正确。

但在logistic回归中，我们不止一个训练样本，而是有很多个训练样本，因此接下来看看如何对m个训练样本进行梯度下降更新。

因为J(w,b)函数是损失函数求和的平均，所以成本函数J(w,b)对w，b的导数也应该是上面推得的式子的求和的平均。

       

根据上面的三个计算导数式子，似乎我们需要编写两层的循环，第一层循环遍历每一个训练样本，第二层循环遍历所有的w参数来进行累加。但当应用深度学习算法时，在代码中显示使用循环是很低效的，尤其是数据量很大的时候。为了避免使用不必要的显示循环，我们需要用到向量化。

向量化

上图是一个求向量内积的例子，可以看到向量化的速度快了不少。这在数据量很大的时候，将更加明显。

在正向传播求z的时候，如果用非向量化实现，那么需要依次分别求解下面的等式，直到第m个训练样本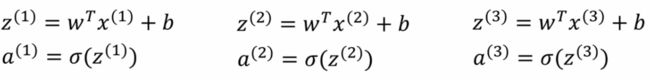

为了使用向量化，我们将用到最开始的矩阵X，X是，表示维度为 x m的矩阵，而w是 x 1的向量，

那么w的转置乘上X矩阵，根据矩阵乘法得到的是一个1xm的矩阵，再加上1xm的b向量，你会发现这个矩阵Z其实就是上面式子的实现

而a其实也是将每个训练样本得到的a进行横向堆叠，

上面是正向传播的向量化过程，下面来看反向传播如何进行向量化。

dz表示成本函数J(w,b)对z求导

同样的思想，将这些z进行横向堆叠得到

接下来需要向量化对每个w参数和对b参数求导的过程

dZ其实就是每个训练样本对b的求导的和，所以在python中，可以用求得db。

dw为，如果展开这个式子其实是

表示第i个训练样本的第j个特征，上面的结果是一个nx x 1的矩阵，而且每一行其实就是对的导数，i为1到nx。

python代码

import numpy as np

def sigmoid(z):
    '''
    σ函数
    '''
    a = 1/(1+np.exp(-z))
    
    return a

def initialize_parameters(dim):
    '''
    初始化w和b参数
    dim: w的维度，在logistic回归中也等于输入特征的数量
    '''
    w = np.random.randn(dim,1)
    b = 0
    
    return w,b

def propagate(w,b,X,Y):
    '''
    正向和反向传播
    
    X:训练集的特征向量 形状为(num_px*num_px*3,m) num_px表示图像的尺寸,m表示训练样本的个数
    Y:训练集的标签 形状为(1,m)
    
    cost:logistic回归的成本函数
    dw:成本函数对w的导数
    db:成本函数对b的导数
    '''
    m = X.shape[1]
    A = sigmoid(np.dot(w.T,X)+b)
    cost = -1/m*np.sum(Y*np.log(A)+(1-Y)*np.log(1-A))
    
    dw = 1/m*np.dot(X,(A-Y).T)
    db = 1/m*np.sum(A-Y)
    
    cost = np.squeeze(cost)
    grads = {"dw":dw,
             "db":db}
    
    return grads,cost

def optimize(w,b,X,Y,num_iterations,learning_rate,print_cost = False):
    '''
    梯度下降算法
    
    num_iterations：迭代次数(梯度下降的次数) 
    learning_rate: 学习率α
    
    costs 记录迭代过程中的代价函数值，用来绘图，便于判断梯度下降是否正确
    '''
    costs = []
    
    for i in range(num_iterations):
        grads,cost = propagate(w,b,X,Y)
        
        dw = grads["dw"]
        db = grads["db"]
        
        w = w - learning_rate*dw
        b = b - learning_rate*db
        
        if i%100 == 0:
            costs.append(cost)
        
        if print_cost and i % 100 == 0:
            print("Cost after iteration %i: %f" %(i, cost))
            
    params = {"w":w,
              "b":b}
    
    grads = {"dw":dw,
             "db":db}
    
    return params,grads,costs

def predict(w,b,X):
    '''
    根据训练得到的w,b进行预测
    '''
    m = X.shape[1]
    A = sigmoid(np.dot(w.T,X)+b)
    Y_prediction = np.zeros((1,m))
    
    for i in range(m):
        Y_prediction[0,i]=A[0,i]>0.5
    
    return Y_prediction

def model(X_train,Y_train,X_test,Y_test,num_iterations = 2000,learning_rate = 0.5,print_cost = False):
    '''
    整合每个函数
    
    X_train 训练集的特征向量
    Y_train 训练集的标签
    X_test 测试集样本的特征向量
    Y_test 测试集样本的标签
    '''
    w,b = initialize_parameters(X_train.shape[0])
    parameters,grads,costs = optimize(w,b,X_train,Y_train,num_iterations,learning_rate,print_cost)
    
    w = parameters["w"]
    b = parameters["b"]
    
    Y_prediction_train = predict(w,b,X_train)
    Y_prediction_test = predict(w,b,X_test)
    
    d = {"costs": costs,
         "Y_prediction_test": Y_prediction_test, 
         "Y_prediction_train" : Y_prediction_train, 
         "w" : w, 
         "b" : b,
         "learning_rate" : learning_rate,
         "num_iterations": num_iterations}
    
    return d