Leetcode单调栈总结
数组之间的元素需要比较时,可以考虑单调栈,典型的以空间换取时间的方法:
因为题目要求,单调栈一般保存的都是索引数组,这点务必注意!
目录
739. 每日温度
84. 柱状图中最大的矩形
42. 接雨水
85. 最大矩形
316. 去除重复字母
402. 移掉K位数字
581. 最短无序连续子数组
739. 每日温度
https://leetcode-cn.com/problems/daily-temperatures/
本题题意英文版更好理解
那么我们很容易想到结题方法:
从该点出发,不断往后遍历,找到第一个比自己大的元素,做差,保存,完成
这是典型的暴力解法,代码如下:
class Solution {
public:
vector dailyTemperatures(vector& T) {
//双指针循环
if(T.empty()) return {};
int size = T.size();
vectorRes;
int begin = 0,right = begin+1;
while(begin=size) Res.push_back(0);
begin++;
}
return Res;
}
}; 显然是会超时的
暴力法进行了很多次的重复操作,这种具有单调性质的题目,我们使用单调栈来完成操作:
我们现在假设,我们从i开始,要在后续数组中,找到第一个比自己大的数值,并计算二者索引的差值,然后保存,如果没有找到,就是0。
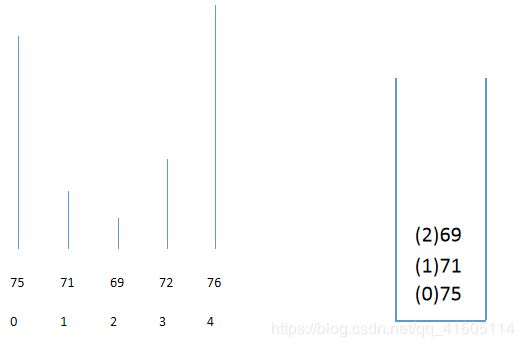
我们完全可以使用一个栈,保持栈内单调递减,也就是说,栈中元素,都没有遇到第一个比自己大的数值,都是等待状态
当遇到一个值大于栈顶元素时,说明栈顶元素已经找到了目标值,做差记录即可,然后弹出,之后重复这个过程
到最后,还留在栈中的元素,说明都没有找到目标值,那么我们全部标记为0即可。
我们来看一下图解:
栈中单调递减,顶部是最小值,下面我们压入72,分别弹出69和71,并让索引做差,得到我们想要的结果
代码完整版本如下:
class Solution {
public:
vector dailyTemperatures(vector& T) {
//双指针循环(超时)
//单调栈
if(T.empty()) return {};
int size = T.size();
vectorRes(size,0);//全部初始化为0
stackS;
for(int i = 0;i
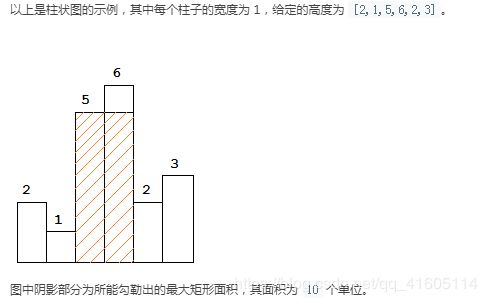
84. 柱状图中最大的矩形
https://leetcode-cn.com/problems/largest-rectangle-in-histogram/
暴力解法:
我们从i处,开始向左右两个方向遍历,找比i的值小的或者相等的高度,然后计算面积,这个过程一定要注意细节:
class Solution {
public:
int largestRectangleArea(vector& heights) {
if(heights.empty()) return 0;
if(heights.size() == 1) return heights[0];
int sum = 0,MAX = 0;
for(int i = 0;i=0&&heights[left]>=heights[i]) left--;
while(i!=heights.size()-1&&right=heights[i])
right++;
sum = heights[i]*(right - left -1);
MAX = max(MAX,sum);
cout< 显然是超时了:
算法参考:https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/zhu-zhuang-tu-zhong-zui-da-de-ju-xing-by-leetcode-/
我们之前计算的结果没有为之后服务
我们在暴力法中,选择一个柱子i,然后左右遍历,寻找比i低的柱子,此目的是为了找到长,然后计算面积
我们来看这个遍历过程,不断右移,遇到比i低的柱子,停止,计算面积
那么我们构造一个单点栈,单调递增,栈中的答案都是以i为高的矩形,长度访问内的内容,换句话说,栈中的元素都是可以作为这个矩形长的一部分的。此时栈中单调递增。
那么什么时候这个长会停止呢?就是当遇到一个比目前栈顶(可能不是i)小的元素,那么我们至少需要对栈顶进行操作
因为对于栈顶来说,以自己为高的矩形,长度方向已经遇到了边界,以高度为i的矩形,不能在向右扩散了,因为遇到了边界。
上面的陈述,让我们找到了右边界,下面我们去寻找左边界
当我们将一个元素压入栈中时,
左侧如此,右侧也是如此,我们看一下图解:
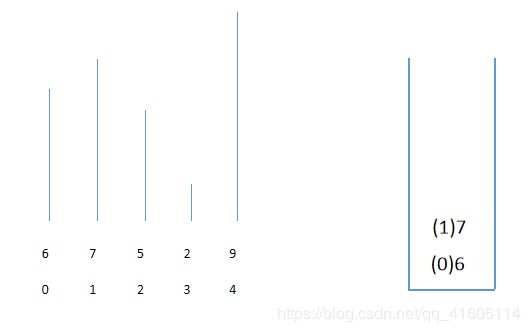
我们以【6,7,5,2,9】为例,现在将6,7压入栈中
因为5的入栈,以6位高度,和以7位高度的矩形,都找到了自己的右边界,直接出栈
往后的过程不再赘述,都是大同小异,那么我们目前只是确定是右边界,还需要确定左区间
我们反向遍历整个数组,尾部元素压入,然后继续压入内容,直到遇到左侧边界,如图,9遇到了2,需要弹出,并记录左边界
同时我们需要注意,最终留在栈中的内容,我们需要处理,说明他们的左或者右边界是整个数组的两端,但是我们这个过程中,都是采用的左右开区间的方式记录,所以让这些值的边界值为-1或者size本身即可。
这个细节务必注意!
完整代码如下:
class Solution {
public:
int largestRectangleArea(vector& heights) {
//两个单调栈的问题
if(heights.empty()) return 0;
int size = heights.size();
vectorRight(size,0),Left(size,0);
stackTemp;
for(int i = 0;iheights[i])//入栈元素小于栈顶元素,需要操作
{
Right[Temp.top()] = i;
Temp.pop();
}
Temp.push(i);
}
//还有残余,说明右边界是size,左边界同理,设置为-1
while(Temp.size()) {Right[Temp.top()] = size;Temp.pop();}
// for(auto item:Right) cout<{};
for(int i = size-1;i>=0;--i)
{
while(Temp.size()&&heights[Temp.top()]>heights[i])//入栈元素小于栈顶元素,需要操作
{
Left[Temp.top()] = i;
Temp.pop();
}
Temp.push(i);
}
//还有残余,说明右边界是size,左边界同理,设置为-1
while(Temp.size()) {Left[Temp.top()] = -1;Temp.pop();}
// for(auto item:Left) cout< 我们能不能再优化?栈是单调递增的
我们什么时候对栈进行出栈操作?是当目前高度小于栈顶高度的时候,我们需要出栈操作
此时我们找到栈顶的右边界
现在思考两个问题,如果只入栈,要入栈元素是i,栈顶是top,top小于等于i:
考虑两个问题:
1:如果i大于栈顶,那么i的左边界就是目前的栈顶,右边界我们会在循环中计算
2:如果i小于栈顶,会一直让栈顶元素弹出,知道遇到比自己小的,那么此时的栈顶,也是i的左边界
3:如果相等,也会入栈,此时左边界无法描述,但是不会影响面积计算
我们对代码进行优化,在计算右边界的时候,就完成左边界的确定
完整代码如下:
class Solution {
public:
int largestRectangleArea(vector& heights) {
//两个单调栈的问题
if(heights.empty()) return 0;
int size = heights.size();
vectorRight(size,0),Left(size,0);
stackTemp;
for(int i = 0;iheights[i])//入栈元素小于栈顶元素,需要操作
{
Right[Temp.top()] = i;
Temp.pop();
}
Left[i] = Temp.empty()?-1:Temp.top();
Temp.push(i);
}
//还有残余,说明右边界是size,左边界同理,设置为-1
while(Temp.size()) {Right[Temp.top()] = size;Temp.pop();}
//最终计算最大面积
int MAXSUM = 0;
for(int i = 0;i 输入数据:
非优化部分:
优化部分:
可以看到,相同内容的边界处理是有问题的,但是不影响整体,是因为有重复元素总有第一次出现的时候,此时就保证了最大面积。
42. 接雨水
https://leetcode-cn.com/problems/trapping-rain-water/
有了上面两道题目的铺垫,本题就看到题目也能想到,我们需要用单调栈进行完成
维护一个单调递减的栈,栈中的元素都是可以组成低洼地区的左边界,那么当下一个我们访问的元素高度高于栈顶元素
那么我们就找到了右边界,此时观察能否组成封闭的低洼地带,下面我们看图解:
当(2)3要入栈的时候,此时我们就可以计算一下低洼地区的面积了,因为栈中单调递减,那么显然top的左侧一定比top高
或者相等,要入栈的元素一定比top大,才会进行这部分操作
所以根据三者索引,计算出长度,再根据i和目前栈顶中的最下值作为低洼地区的边界,得到了高,完成计算
关于相等的问题:
完成上图操作后,整个柱状图变成下面的样子
因为不是严格单调递减,相等的情况出现,在红框的范围内,无法形成低洼,因为没有左边界,直到(3)2出栈
s和top如图所示的时候才能形成低洼
整个过程对程序没有什么影响,因为会选择s和i中小的为边界与top做差,相等的这种情况就是让和为0而已:
被计算过的面积也不会被重复计算,因为目标已经出栈,最低点将会在剩余的部分产生,可以理解为计算过的低洼被填平
下面我们来看整段代码:
class Solution {
public:
int trap(vector& height) {
//单调栈
if(height.empty()) return 0;
int size = height.size();
stacktemp;
int SUM = 0;
for(int i = 0;i
85. 最大矩形
https://leetcode-cn.com/problems/maximal-rectangle/
本题第一眼很像网格dps类型的题目,但是读完题目会发现截然不同
算法参考:https://leetcode-cn.com/problems/maximal-rectangle/solution/zui-da-ju-xing-by-leetcode/
本题实质上和84题很相似,我们可以将本题转化为第84题
我们再看84题:
本题:
联系:
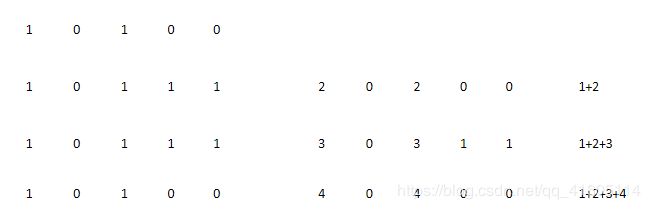
如果我们将本题的数,按列加和,得到结果如图所示,那么就是是第84题了
我们按行加,第一行尾起始,我们计算最大面积,然后第一行累加第二行,当列以0结尾的时候,我们放弃整个列,让其为0
不是0,那么我们累加,效果图如下:
此段程序如下:
for(int i = 0;i我们对没行的处理和第84题一样,下面程序选择了优化后的版本
完整代码:
class Solution {
public:
int maximalRectangle(vector>& matrix) {
if(matrix.empty()) return 0;
int MAX = 0;
int size = matrix[0].size();
vectordp(size,0);
for(int i = 0;i Num)
{
for(auto item:Num) cout<Temp;
vectorRight(size,0),Left(size,0);//记录左右边界
for(int i = 0;i
316. 去除重复字母
https://leetcode-cn.com/problems/remove-duplicate-letters/
class Solution {
public:
string removeDuplicateLetters(string s) {
unordered_map M;
for(auto item:s) M[item]++;
string Res;
for(auto item:s)
{
if(M[item] == 1) Res+=item;
else M[item]--;
}
return Res;
}
}; https://leetcode-cn.com/problems/remove-duplicate-letters/solution/zhan-by-liweiwei1419/
题目解释:关于字典序
比两个字符串的第一个数字,相等,则比较第二个数字,不等,谁小谁的字典序小,不用往后比较。
从简单到难,来找到本题的突破点:
如果输入bca,结果如下:
虽然按照字典序,最优解是abc,但是bc都出现在a前面,且没有在a后面出现,只能是bca
那么如果是bcab,那么我们输出什么?输出:bca,因为b在a后面出现了,目前有两种方案
1:bca
2:cab
显然第一种组合字典序最小
如果输入bcabc,那么最小的字典序就是abc
所以,我们需要知道,某个元素,出现在字符串中的最后位置!
那么我们构建一个栈,压入元素的时候,先判断这个元素的最后位置是不是当前的访问位置
如果是,那么我们没有选择,必须压入栈中
如果不是,那么我们和栈顶元素比大小,将小的放入,(前提是栈顶元素还会在后面出现,否则不能出栈)
构成一个单点递增的栈
图源及思路来源:https://leetcode-cn.com/problems/remove-duplicate-letters/solution/zhan-by-liweiwei1419/
class Solution {
public:
string removeDuplicateLetters(string s) {
if(s.empty()) return "";
unordered_mapLast;//记录每个元素最后出现的索引位置
unordered_mapUsed;//记录该元素是否在目前的栈中
int size = s.size();
for(int i = 0;iTemp;
for(int i = 0;ii)//栈顶元素后面还会出现
{
Used[Temp.top()]=0;
Temp.pop();
}
else break;//栈顶元素后面不会出现,只能压入
}
Temp.push(s[i]);
Used[s[i]]=1;//记录该内容已经被访问
}
vectorResTemp;
while(Temp.size()) {ResTemp.push_back(Temp.top());Temp.pop();}
string Res;
for(int i = ResTemp.size()-1;i>=0;--i) Res += ResTemp[i];
return Res;
}
};
402. 移掉K位数字
https://leetcode-cn.com/problems/remove-k-digits/
思路参考:https://leetcode-cn.com/problems/remove-k-digits/solution/yi-diao-kwei-shu-zi-by-leetcode/
如果一串数字,完全升序递增排列:12345
那么我们拿走一个数字,让剩下数字的组合最小
1:1234
2:2345
3:1345
4:1245
5:1235
显然我们拿走最后一位即可,既可以得到最小的值
下面我们来看例子2:482
我们拿走一个数字,42,82,48,显然拿走8后得到最小值
那么我们可以如此,有一串字符,i,i+1,....;如果i+1小于或者等于i,那么i将会被删除,如果整个数组单调递增,那么直接删除末尾元素
我们需要注意几个细节:
1:当删除完了全部数字,或者只剩下了0,那么我们需要返回“0”,而不是“”;
2:例如10100,删除一个,我们删除的第一个‘1’,那么我们剩下:“0100”,显然我们需要的是剔除第一个无效的0
方法,就是在压入的时候就避免,当栈空,且入栈是0,那么显然是一个无效的前置零,我们直接不进行压入操作
3:当完成删除时,我们需要考虑两个因素,有没有完全删除k个值,k可能还有残留,我们需要从栈的顶部开始进行删除,知道k为0
4:当完成删除时,我们需要考虑,如果是k = 0让循环break,那么我们应该将剩余数组重新压入栈中,保证数据的完整性
完整代码如下:
class Solution {
public:
string removeKdigits(string num, int k) {
if(k == 0) return num;
if(num.empty()) return "";
int size = num.size();
if(k>=size) return "0";//大于等于都是返回
stackTemp;
int Cut = k;
int i;
for(i = 0;i0&&Temp.size()&&num[i]0) {Temp.pop();Cut--;}//从尾部弹出元素
//反转及拷贝内容:
vectorStemp;
while(Temp.size()){Stemp.push_back(Temp.top());Temp.pop();}
string Res;
for(int i = Stemp.size()-1;i>=0;--i) Res+=Stemp[i];
return Res == ""?"0":Res;//如果全部删除或者10,删除了1,那么Res是空,此时我们需要返回0
}
};
581. 最短无序连续子数组
https://leetcode-cn.com/problems/shortest-unsorted-continuous-subarray/