矩阵连乘问题

动态规划算法的基本要素

• 最优子结构性质
• 重叠子问题性质

设计动态规划算法的步骤

• 找出最优解的性质，并刻划其结构特征
• 递归地定义最优值
• 以自底向上的方式计算出最优值
• 根据计算最优值时得到的信息，构造最优解

分析最优解的结构特征

假设我们已经知道了在第 $k$ 个位置加括号会得到最优解，那么原问题就变成了两个子问题：$(A_i{A}_{i+1}...A_k)$，$(A_{k+1}{A}_{k+2}...A_j)$， 如下图所示。

原问题的最优解是否包含子问题的最优解呢？

假设 $(A_i{A}_{i+1}...A_j)$ 的乘法次数是 $c$ ，$(A_i{A}_{i+1}...A_k)$ 的乘法次数是 $a$，$(A_{k+1}{A}_{k+2}...A_j)$ 的乘法次数是 $b$，$(A_i{A}_{i+1}...A_k)$ 和 $(A_{k+1}{A}_{k+2}...A_j)$ 的结果矩阵相乘的乘法次数是 $d$，那么 $c=a+b+d$，无论两个子问题 $(A_i{A}_{i+1}...A_k)$、 $(A_{k+1}{A}_{k+2}...A_j)$ 的计算次序如何，都不影响它们结果矩阵，两个结果矩阵相乘的乘法次数 $d$ 不变。

因此，我们只需要证明如果 $c$ 是最优的，则 $a$ 和 $b$ 一定是最优的（即原问题的最优解包含子问题的最优解）。

反证法：如果 $a$ 不是最优的，$(A_i{A}_{i+1}...A_k)$ 存在一个最优解 $a^{\prime }$，$a^{\prime }<a$，那么，$a^{\prime }+b+d<c$，所以 $c$ 不是最优的，这与假设 $c$ 是最优的矛盾，因此如果 $c$ 是最优的，则 $a$ 一定是最优的。同理可证 $b$ 也是最优的。因此如果 $c$ 是最优的，则 $a$ 和 $b$ 一定是最优的。

因此，矩阵连乘问题具有最优子结构性质。

建立最优值递归式

可以递归地定义 $m[i,j]$ 为：
​
$$m[i][j]=\{\begin{array}{ll}0,& i=j\\ \underset{i\le k<j}{\min }\left\{m[i][k]+m[k+1][j]+p[i-1]\ast p[k]\ast p[j]\right\},& i<j\end{array}$$

计算出最优值

这里以 AIZU 的 Matrix-chain Multiplication 为例，题目链接：点击这里

递归（自顶向下）

计算 $A[1...4]$ 的递归树如下图所示：

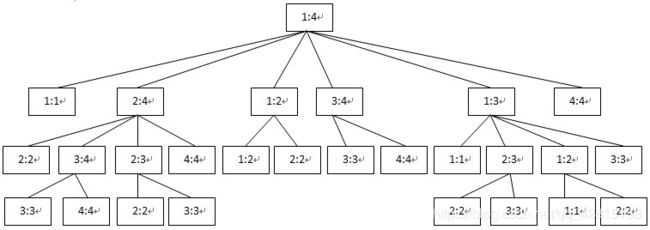
从上图可以看出很多子问题被重复运算。可以证明，该算法的计算时间 $T(n)$ 有指数下界。设算法中判断语句和赋值语句为常数时间，则由算法的递归部分可得关于 $T(n)$ 的递归不等式：

用数学归纳法可以证明 $T(n)\ge 2^{n-1}$，因此，重叠递归的计算时间随 $n$ 指数增长。

TLE代码：

#include
#include
#include

using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 110;

int n;
int p[N];

int fun(int l, int r)
{
	if(l == r)	return 0;
	
	int minn = INF;
	for(int k = l; k < r; k++)
	{
		int t = fun(l, k) + fun(k + 1, r) + p[l-1] * p[k] * p[r];
		if(t < minn)	minn = t;
	}
	
	return minn;
}

int main()
{
	scanf("%d", &n);
	for(int i = 1; i <= n; i++)	scanf("%d%d", &p[i-1], &p[i]);
	
	printf("%d\n", fun(1, n));
	
	return 0;
}

备忘录（自顶向下）

AC代码：

#include
#include
#include

using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 110;

int n;
int p[N];
int f[N][N];

int fun(int l, int r)
{
	if(f[l][r])	return f[l][r];
	
	if(l == r)	return 0;
	
	int minn = INF;
	for(int k = l; k < r; k++)
	{
		int t = fun(l, k) + fun(k + 1, r) + p[l-1] * p[k] * p[r];
		if(t < minn)	minn = t;
	}
	
	return f[l][r] = minn;
}

int main()
{
	scanf("%d", &n);
	for(int i = 1; i <= n; i++)	scanf("%d%d", &p[i-1], &p[i]);
	
	printf("%d\n", fun(1, n));
	
	return 0;
}

动态规划（自底向上）

AC代码：

#include
#include
#include

using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 110;

int n;
int p[N];
int f[N][N];

int main()
{
	scanf("%d", &n);
	for(int i = 1; i <= n; i++)	scanf("%d%d", &p[i-1], &p[i]);
	
	for(int len = 2; len <= n; len++)
	{
		for(int i = 1; i + len - 1 <= n; i++)
		{
			int j = i + len - 1;
			f[i][j] = INF;
			for(int k = i; k < j; k++)
				f[i][j] = min(f[i][j], f[i][k] + f[k+1][j] + p[i-1] * p[k] * p[j]);
		}
	}
	
	printf("%d\n", f[1][n]);
	
	return 0;
}

构造出最优解

上面得到的最优值只是矩阵连乘的最小的乘法次数，并不知道加括号的次序，需要从记录表中还原加括号次序，构造出最优解。

用二维数组 $s[][]$ 来存放各个子问题的最优决策（即加括号的位置）。

根据最优决策信息数组 $s[][]$ 递归构造最优解：

• $s[1][n]$ 表示 $A_1{A}_2...A_n$ 最优解的加括号位置，即 $(A_1{A}_2...A_{s[1][n]})(A_{s[1][n]+1}...A_n)$
• 再递归构造两个子问题 $(A_1{A}_2...A_{s[1][n]})$、$(A_{s[1][n]+1}...A_n)$ 的最优解加括号位置
• 一直递归到子问题只包含一个矩阵为止。

在备忘录的代码基础上构造出最优解：

#include
#include
#include

using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 110;

int n;
int p[N];
int f[N][N];
int s[N][N];

int fun(int l, int r)
{
	if(f[l][r])	return f[l][r];
	
	if(l == r)	return 0;
	
	int minn = INF;
	for(int k = l; k < r; k++)
	{
		int t = fun(l, k) + fun(k + 1, r) + p[l-1] * p[k] * p[r];
		if(t < minn)
		{
			minn = t;
			s[l][r] = k;						// 记录决策信息 
		}
	}
	
	return f[l][r] = minn;
}

void print(int i, int j)
{
    if(i == j)
    {
		printf("A[%d]", i);
		return;
    }
    printf("(");
    print(i, s[i][j]);
    print(s[i][j] + 1, j);
    printf(")");
}

int main()
{
	scanf("%d", &n);
	for(int i = 1; i <= n; i++)	scanf("%d%d", &p[i-1], &p[i]);
	
	printf("%d\n", fun(1, n));
	
	print(1, n);								// 输出路径 
	
	return 0;
}

在动态规划的代码基础上构造出最优解：

#include
#include
#include

using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 110;

int n;
int p[N];
int f[N][N];
int s[N][N];

void print(int i, int j)
{
    if(i == j)
    {
		printf("A[%d]", i);
		return;
    }
    printf("(");
    print(i, s[i][j]);
    print(s[i][j] + 1, j);
    printf(")");
}

int main()
{
	scanf("%d", &n);
	for(int i = 1; i <= n; i++)	scanf("%d%d", &p[i-1], &p[i]);
	
	for(int len = 2; len <= n; len++)
	{
		for(int i = 1; i + len - 1 <= n; i++)
		{
			int j = i + len - 1;
			f[i][j] = INF;
			for(int k = i; k < j; k++)
			{
				int t = f[i][k] + f[k+1][j] + p[i-1] * p[k] * p[j];
				if(t < f[i][j])
				{
					f[i][j] = t;
					s[i][j] = k;				// 记录最优决策 
				}
			}
		}
	}
	
	printf("%d\n", f[1][n]);
	
	print(1, n);								// 输出路径 
	
	return 0;
}

过程图解

矩阵连乘动态规划的过程图解（帮助理解）：

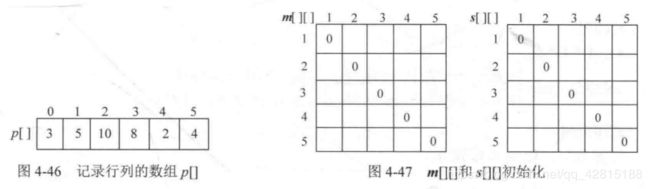
初始化：

计算 $2$ 个矩阵相乘的最优值：

计算 $3$ 个矩阵相乘的最优值：

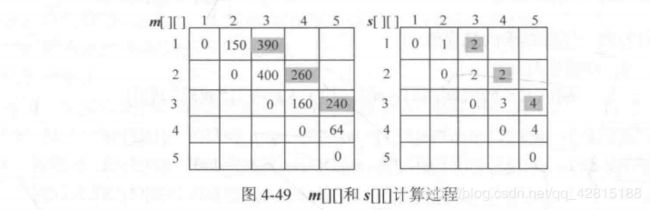
计算 $4$ 个矩阵相乘的最优值：

计算 $5$ 个矩阵相乘的最优值：

构造最优解过程：