第五章 线性系统的频域分析
目录
5.1 频率特性的概念
5.2 典型环节的频率特性
5.3 系统的开环频率特性
5.4 奈奎斯特稳定判据和系统的相对稳定性
5.5 利用开环频率特性分析系统性能
5.6 利用闭环频率特性分析系统性能
本章重点
1 开环频率特性的绘制(包括极坐标图和对数坐标图)
2 奈奎斯特稳定性判据及其在Bode图中的应用
3 对数频率特性和闭环系统性能的关系
4 开环频率特性指标
5 闭环频率特性指标
本章难点
1 开环频率特性的绘制
2 奈奎斯特判据的原理及其应用
3 剪切频率及相角、幅值裕度的求取
4 二阶系统频率特性指标和时域性能指标的换算
5 典型二型系统频、时域指标的定性关系
5.1 频率特性的概念
5.1.1 频率特性的定义
线性定常系统(或元件)的频率特性是指:在零初始条件下,稳态输出的正弦信号与输入正弦信号的复数比。可分为幅频特性和相频特性。
5.1.2 频率特性与传递函数的关系
频率特性和传递函数的关系为:
G ( s ) ∣ s = j ω = G ( j ω ) ; G(s)|_{s=j\omega}=G(j\omega); G(s)∣s=jω=G(jω);
系统的频率特性也是输入信号的傅氏变换和输出信号的傅氏变换之比,即:
G ( j ω ) = C ( j ω ) R ( j ω ) G(j\omega)=\frac{C(j\omega)}{R(j\omega)} G(jω)=R(jω)C(jω)
5.1.2 频率特性的几种图示方法
(1)幅相频率特性曲线
在复平面上以极坐标的形式来描述,又称极坐标图,或者称Nyquist图。实频特性是ω的偶函数,虚频特性是ω的奇函数。
- 系统的频率特性可表示为: G ( j ω ) = A ( ω ) e j ϕ ( ω ) G(j\omega)=A(\omega)e^{j\phi(\omega)} G(jω)=A(ω)ejϕ(ω)
- 对某一固定频率ω1,则: G ( j ω 1 ) = A ( ω 1 ) e j ϕ ( ω 1 ) G(j\omega_1)=A(\omega_1)e^{j\phi(\omega_1)} G(jω1)=A(ω1)ejϕ(ω1)
- 在极坐标系中画出该向量。
- ω从-∞→+∞变换时,该向量在极坐标系中形成的曲线。

(2)对数频率特性曲线(Bode图)
在半对数坐标纸上绘制,由对数幅频特性和对数相频特性两条曲线所组成。其中对数幅频特性是指 G ( j ω ) G(j\omega) G(jω)的对数值 20 l g ∣ G ( j ω ) ∣ 20lg|G(j\omega)| 20lg∣G(jω)∣和频率 ω \omega ω的关系曲线,即纵坐标 L ( ω ) = 20 l g A ( ω ) L(\omega)=20lgA(\omega) L(ω)=20lgA(ω),单位是dB(分贝);对数相频特性是指 G ( j ω ) G(j\omega) G(jω)的相角值 ϕ ( ω ) \phi(\omega) ϕ(ω)和频率 ω \omega ω的关系曲线,纵坐标的单位是度,线性刻度。
(3)对数幅相特性曲线(Nichols图)
5.2 典型环节的频率特性
典型环节的幅相频率特性求取步骤:
求环节或系统的传递函数G(s);
令s=jω,求出频率特性表达式G(jω);
G(jω)分为实部P(ω)和虚部Q(ω),若G(jω)的分母为复数或虚数,需要进行有理化处理;
求出幅频和相频特性A(ω)和φ(ω)的表达式,根据不同的ω值计算,在极坐标上描点,绘制成曲线。
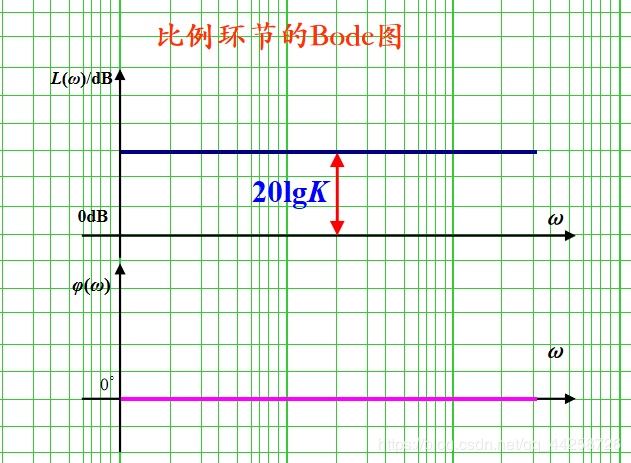
5.2.1 比例环节
比例环节传递函数为: G ( s ) = K = c o n s t G(s)=K=const G(s)=K=const 频率特性表达式为: G ( s ) = K = c o n s t G(s)=K=const G(s)=K=const 则 P ( ω ) = K = c o n s t , Q ( ω ) = 0 P(\omega)=K=const,Q(\omega)=0 P(ω)=K=const,Q(ω)=0 A ( ω ) = K = c o n s t , ϕ ( ω ) = a r c t a n 0 K = 0 。 A(\omega)=K=const,\phi(\omega)=arctan{0\over K}=0^。 A(ω)=K=const,ϕ(ω)=arctanK0=0。

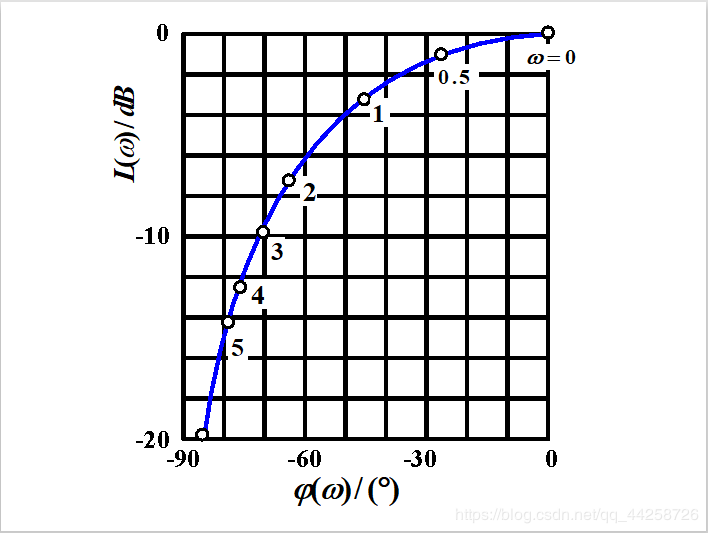
5.2.2 惯性环节
惯性环节传递函数为: G ( s ) = 1 1 + τ s G(s)={1\over{1+\tau s}} G(s)=1+τs1 频率特性表达式为:
G ( j ω ) = 1 1 + j ω τ G(j\omega)={1\over{1+j\omega\tau}} G(jω)=1+jωτ1 则 P ( ω ) = 1 1 + τ 2 ω 2 , Q ( ω ) = − τ ω 1 + τ 2 ω 2 P(\omega)={1\over1+\tau^2\omega^2},Q(\omega)={-\tau\omega\over1+\tau^2\omega^2} P(ω)=1+τ2ω21,Q(ω)=1+τ2ω2−τω A ( ω ) = 1 1 + ω 2 τ 2 , ϕ ( ω ) = − a r c t a n ω τ A(\omega)={1\over \sqrt{{1+\omega^2\tau^2}}},\phi(\omega)=-arctan{\omega\tau} A(ω)=1+ω2τ21,ϕ(ω)=−arctanωτ


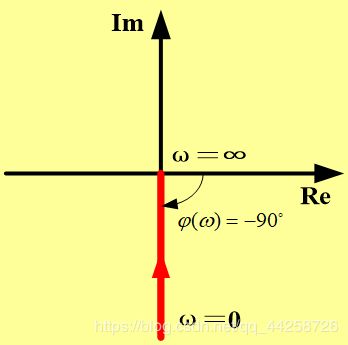
5.2.3 积分环节
积分环节传递函数为: G ( s ) = 1 s G(s)={1\over{s}} G(s)=s1 频率特性表达式为:
G ( j ω ) = 1 j ω = − j 1 ω = 1 ω e − j π 2 G(j\omega)={1\over{j\omega}}=-j{1\over\omega}={1\over\omega}e^{-j{\pi\over2}} G(jω)=jω1=−jω1=ω1e−j2π 则
P ( ω ) = 0 , Q ( ω ) = − 1 ω P(\omega)=0,Q(\omega)=-{1\over\omega} P(ω)=0,Q(ω)=−ω1 A ( ω ) = 1 ω , ϕ ( ω ) = − 9 0 。 A(\omega)={1\over\omega},\phi(\omega)=-90^。 A(ω)=ω1,ϕ(ω)=−90。

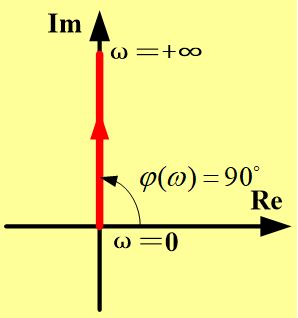
5.2.4 微分环节
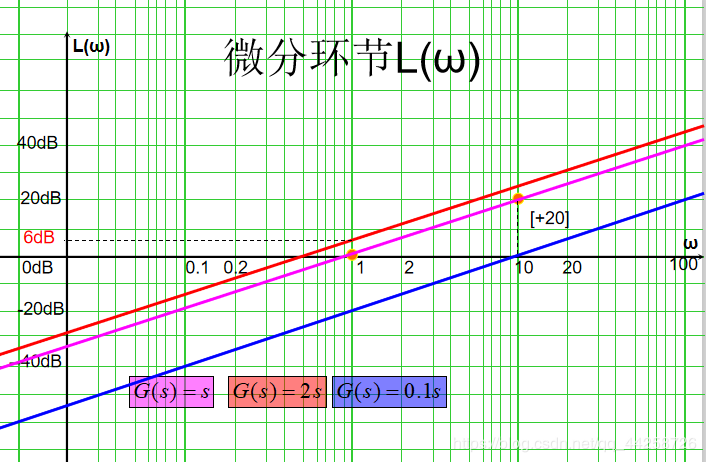
(1) 纯微分环节
积分环节传递函数为: G ( s ) = s G(s)=s G(s)=s 频率特性表达式为:
G ( j ω ) = j ω = ω e j π 2 G(j\omega)={{j\omega}}={\omega}e^{j{\pi\over2}} G(jω)=jω=ωej2π则 P ( ω ) = 0 , Q ( ω ) = ω P(\omega)=0,Q(\omega)={\omega} P(ω)=0,Q(ω)=ω A ( ω ) = ω , ϕ ( ω ) = 9 0 。 A(\omega)={\omega},\phi(\omega)=90^。 A(ω)=ω,ϕ(ω)=90。
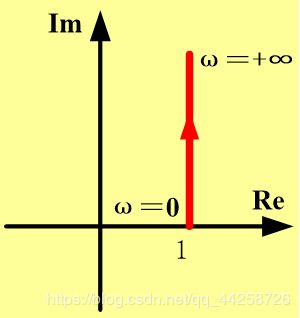
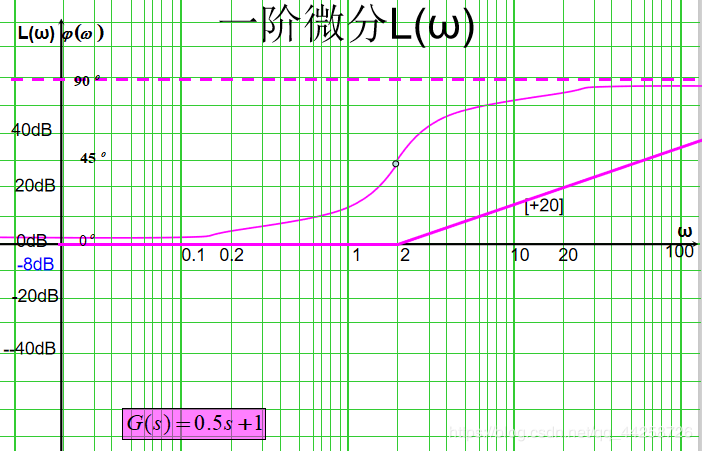
(2) 一阶微分环节
积分环节传递函数为:
G ( s ) = 1 + τ s G(s)=1+\tau s G(s)=1+τs 频率特性表达式为:
G ( j ω ) = 1 + j τ ω G(j\omega)={1+{j\tau\omega}} G(jω)=1+jτω 则 P ( ω ) = 1 , Q ( ω ) = ω τ P(\omega)=1,Q(\omega)={\omega\tau} P(ω)=1,Q(ω)=ωτ A ( ω ) = 1 + ω 2 τ 2 , ϕ ( ω ) = a r c t a n ω τ A(\omega)=\sqrt{{1+\omega^2\tau^2}},\phi(\omega)=arctan{\omega\tau} A(ω)=1+ω2τ2,ϕ(ω)=arctanωτ
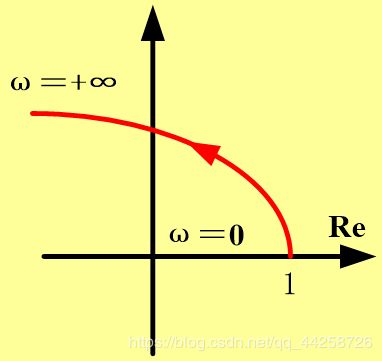
(3) 二阶微分环节
积分环节传递函数为:
G ( s ) = 1 + 2 ξ τ s + τ 2 s 2 G(s)=1+2\xi\tau s+\tau^2s^2 G(s)=1+2ξτs+τ2s2 频率特性表达式为:
G ( j ω ) = 1 + 2 ξ τ ( j ω ) + τ 2 ( j ω ) 2 G(j\omega)=1+2\xi\tau (j\omega)+\tau^2(j\omega)^2 G(jω)=1+2ξτ(jω)+τ2(jω)2 则 P ( ω ) = 1 − ω 2 τ 2 , Q ( ω ) = 2 ξ τ ω P(\omega)={{1-\omega^2\tau^2}},Q(\omega)=2\xi\tau \omega P(ω)=1−ω2τ2,Q(ω)=2ξτω L ( ω ) = 20 l g ( 1 − ω 2 τ 2 ) 2 + ( 2 ξ ω τ ) 2 L(\omega)=20lg\sqrt{{(1-\omega^2\tau^2)^2+(2\xi\omega\tau)^2}} L(ω)=20lg(1−ω2τ2)2+(2ξωτ)2 ϕ ( ω ) = a r c t a n ( 2 ξ ω τ 1 − ω 2 τ 2 ) , ω ≤ 1 τ \phi(\omega)=arctan({2\xi\omega\tau\over{1-\omega^2\tau^2}}), \omega\leq{1\over\tau} ϕ(ω)=arctan(1−ω2τ22ξωτ),ω≤τ1 ϕ ( ω ) = a r c t a n ( 2 ξ ω τ 1 − ω 2 τ 2 ) + π , ω > 1 τ \phi(\omega)=arctan({2\xi\omega\tau\over{1-\omega^2\tau^2}})+\pi, \omega>{1\over\tau} ϕ(ω)=arctan(1−ω2τ22ξωτ)+π,ω>τ1

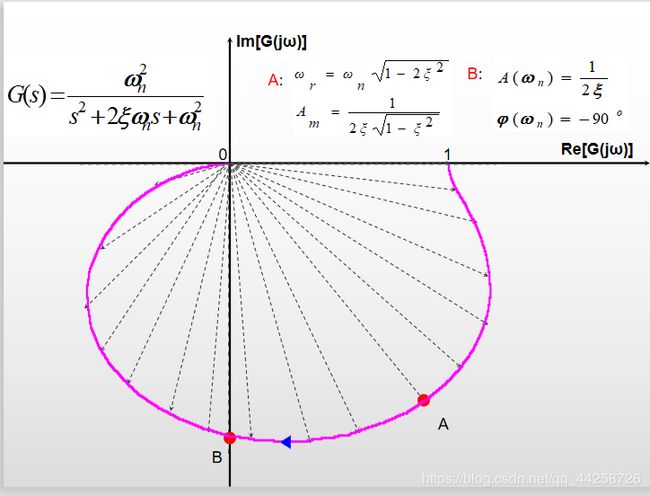
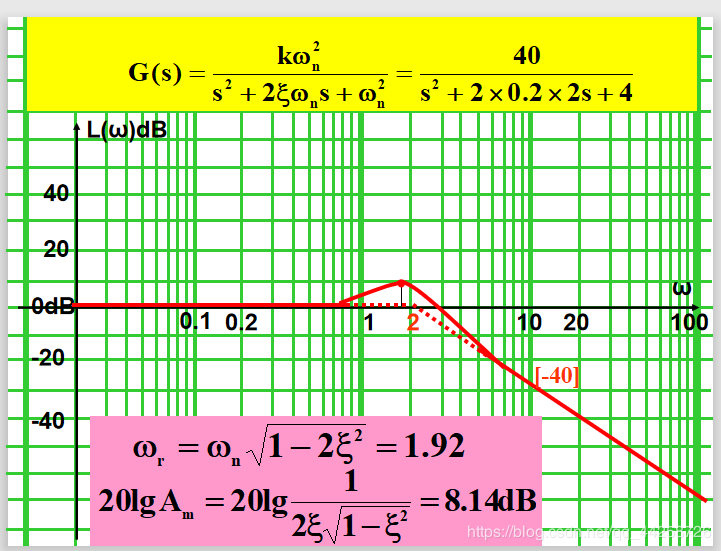
5.2.5 振荡环节
积分环节传递函数为:
G ( s ) = 1 1 + 2 ξ τ s + τ 2 s 2 = ω n 2 ω n 2 + 2 ξ ω n s + s 2 , ω n = 1 τ G(s)={1\over{1+2\xi\tau s+\tau^2s^2}}={{\omega_n}^2\over{{\omega_n}^2+2\xi{\omega_n} s+s^2}},\omega_n={1\over\tau} G(s)=1+2ξτs+τ2s21=ωn2+2ξωns+s2ωn2,ωn=τ1 频率特性表达式为:
G ( j ω ) = 1 1 − τ 2 ω 2 + j 2 ξ ω τ G(j\omega)={1\over{1-\tau^2\omega^2+j2\xi\omega\tau}} G(jω)=1−τ2ω2+j2ξωτ1 则 A ( ω ) = 1 ( 1 − τ 2 ω 2 ) 2 + ( 2 ξ ω τ ) 2 A(\omega)={1\over\sqrt{(1-\tau^2\omega^2)^2+(2\xi\omega\tau)^2}} A(ω)=(1−τ2ω2)2+(2ξωτ)21 ϕ ( ω ) = − a r c t a n ( 2 ξ ω τ 1 − ω 2 τ 2 ) , ω ≤ 1 τ \phi(\omega)=-arctan({2\xi\omega\tau\over{1-\omega^2\tau^2}}), \omega\leq{1\over\tau} ϕ(ω)=−arctan(1−ω2τ22ξωτ),ω≤τ1 ϕ ( ω ) = − a r c t a n ( 2 ξ ω τ 1 − ω 2 τ 2 ) − π , ω > 1 τ \phi(\omega)=-arctan({2\xi\omega\tau\over{1-\omega^2\tau^2}})-\pi, \omega>{1\over\tau} ϕ(ω)=−arctan(1−ω2τ22ξωτ)−π,ω>τ1
5.2.6 滞后环节
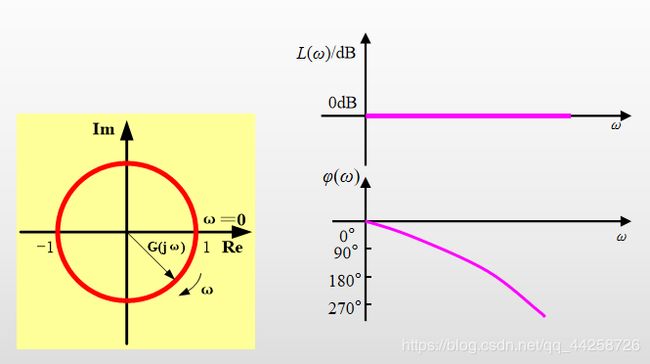
积分环节传递函数为:
G ( s ) = e − τ s G(s)=e^{-\tau s} G(s)=e−τs 频率特性表达式为:
G ( j ω ) = e − j τ ω G(j\omega)=e^{-j\tau \omega} G(jω)=e−jτω 则 A ( ω ) = 1 A(\omega)=1 A(ω)=1 ϕ ( ω ) = − τ ω \phi(\omega)=-\tau\omega ϕ(ω)=−τω
5.3 系统的开环频率特性
5.3.1系统开环幅相特性的绘制
绘制开环极坐标图时应注意的特征:
ω→0时,低频段从何处出发?
ω→∞时,高频段以何种姿态趋近原点?
曲线在ω为何值时穿越实轴和虚轴?穿越的坐标值为多少?
G ( j ω ) = K ( j ω ) ν . ∏ i = 1 m 1 ( j τ i ω + 1 ) ∏ k = 1 m 2 [ τ k 2 ( j ω ) 2 + 2 ξ k τ k ( j ω ) + 1 ] ∏ j = 1 n 1 ( j τ j ω + 1 ) ∏ l = 1 n 2 [ τ l 2 ( j ω ) 2 + 2 ξ l τ l ( j ω ) + 1 ] G(j\omega)={K\over(j\omega)^\nu} .{\prod_{i=1}^{m_1}{(j\tau_i\omega+1)} \prod_{k=1}^{m_2}{[{\tau_k}^2(j\omega)^2+2\xi_k\tau_k(j\omega)+1]}\over{\prod_{j=1}^{n_1}{(j\tau_j\omega+1)} \prod_{l=1}^{n_2}{[{\tau_l}^2(j\omega)^2+2\xi_l\tau_l(j\omega)+1]}}} G(jω)=(jω)νK.∏j=1n1(jτjω+1)∏l=1n2[τl2(jω)2+2ξlτl(jω)+1]∏i=1m1(jτiω+1)∏k=1m2[τk2(jω)2+2ξkτk(jω)+1] m 1 + 2 m 2 = m , n 1 + 2 n 2 + ν = n , n ≥ m m_1+2m_2=m,n_1+2n_2+\nu=n,n\geq m m1+2m2=m,n1+2n2+ν=n,n≥m
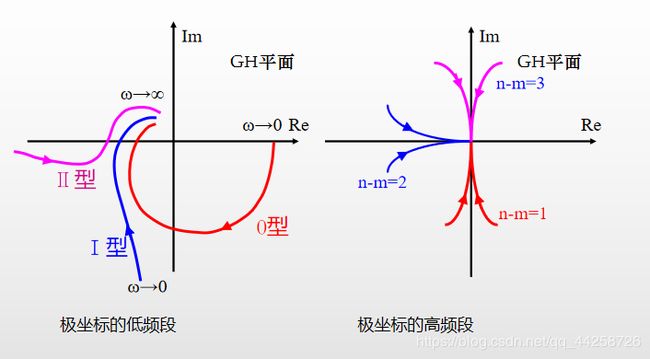
ω → 0 \omega\rightarrow0 ω→0时,低频段的表达式为 G ( j ω ) = K ( j ω ) ν G(j\omega)={K\over(j\omega)^\nu} G(jω)=(jω)νK幅频和相频表达式分别为: A ( ω ) = K ω ν , ϕ ( ω ) = − ν π 2 A(\omega)={K\over\omega^\nu},\phi(\omega)=-\nu{\pi\over2} A(ω)=ωνK,ϕ(ω)=−ν2π
ω → ∞ \omega\rightarrow∞ ω→∞时,高频段的幅频和相频特性为: l i m ω → ∞ ∣ G ( j ω ) ∣ = 0 , l i m ω → ∞ ∠ G ( j ω ) = − ( n − m ) π 2 lim_{\omega\rightarrow∞}|G(j\omega)|=0,lim_{\omega\rightarrow∞}\angle G(j\omega)=-(n-m){\pi\over2} limω→∞∣G(jω)∣=0,limω→∞∠G(jω)=−(n−m)2π

5.3.2系统开环对数频率特性的绘制
1.对数幅频特性的绘制
步骤
求出低频渐近线的斜率和位置。
再确定转折频率和转折直线的斜率。
由低频到高频绘出开环频率特性。
(1) 低频渐近线的绘制
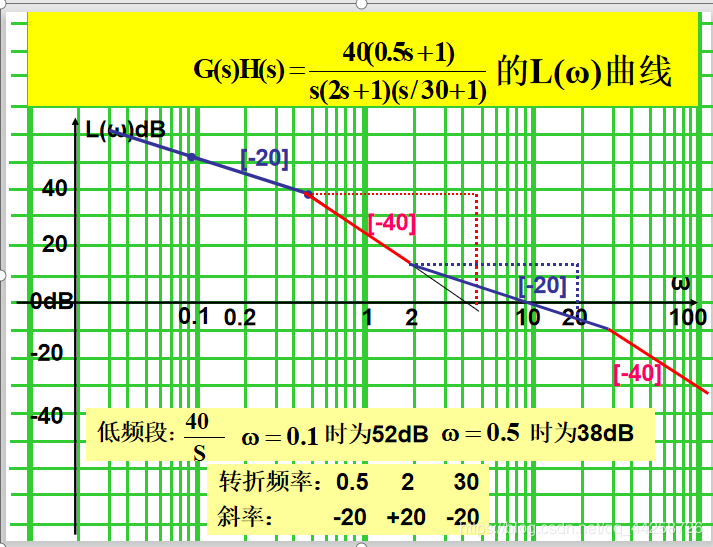
低频渐近线(或延长线)在 ω = 1 ω=1 ω=1处的高度为 20 l g K ( d B ) 20lgK(dB) 20lgK(dB),K是开环传函放大系数。与0dB相交点的频率为 K 1 / ν K^{1/\nu} K1/ν。低频渐近线的斜率为 - 20 ν ( d B / d e c ) -20\nu(dB/dec) -20ν(dB/dec),v是开环系统型别(串联积分环节个数)。
(2) 转折频率及转折后斜率变化量的确定
G ( j ω ) = K ( j ω ) ν . ∏ i = 1 m 1 ( j τ i ω + 1 ) ∏ k = 1 m 2 [ τ k 2 ( j ω ) 2 + 2 ξ k τ k ( j ω ) + 1 ] ∏ j = 1 n 1 ( j τ j ω + 1 ) ∏ l = 1 n 2 [ τ l 2 ( j ω ) 2 + 2 ξ l τ l ( j ω ) + 1 ] G(j\omega)={K\over(j\omega)^\nu} .{\prod_{i=1}^{m_1}{(j\tau_i\omega+1)} \prod_{k=1}^{m_2}{[{\tau_k}^2(j\omega)^2+2\xi_k\tau_k(j\omega)+1]}\over{\prod_{j=1}^{n_1}{(j\tau_j\omega+1)} \prod_{l=1}^{n_2}{[{\tau_l}^2(j\omega)^2+2\xi_l\tau_l(j\omega)+1]}}} G(jω)=(jω)νK.∏j=1n1(jτjω+1)∏l=1n2[τl2(jω)2+2ξlτl(jω)+1]∏i=1m1(jτiω+1)∏k=1m2[τk2(jω)2+2ξkτk(jω)+1]
- ω i = 1 τ i \omega_i={1\over\tau_i} ωi=τi1,经过 ω i \omega_i ωi后,斜率变化量为 + 20 ν ( d B / d e c ) +20\nu(dB/dec) +20ν(dB/dec)。
-. ω k = 1 τ k \omega_k={1\over\tau_k} ωk=τk1,经过 ω k \omega_k ωk后,斜率变化量为 + 40 ν ( d B / d e c ) +40\nu(dB/dec) +40ν(dB/dec)。 - ω j = 1 τ j \omega_j={1\over\tau_j} ωj=τj1,经过 ω j \omega_j ωj后,斜率变化量为 − 20 ν ( d B / d e c ) -20\nu(dB/dec) −20ν(dB/dec)。
- ω l = 1 τ l \omega_l={1\over\tau_l} ωl=τl1,经过 ω l \omega_l ωl后,斜率变化量为 − 40 ν ( d B / d e c ) -40\nu(dB/dec) −40ν(dB/dec)。
2.对数相频特性的绘制
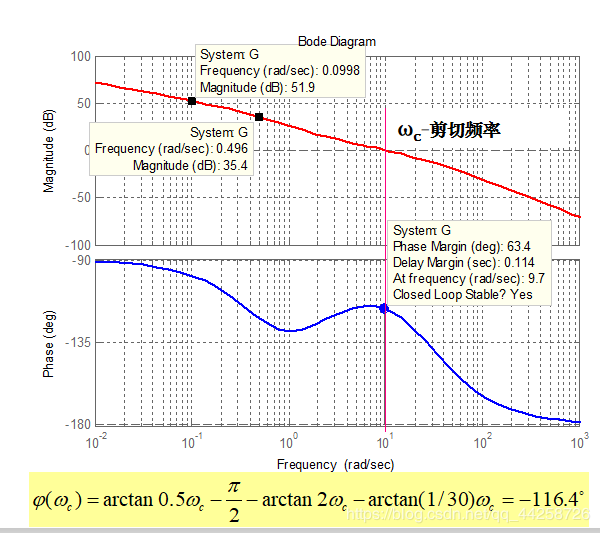
相频特性的表达式为: ϕ ( ω ) = ∑ i = 1 m 1 arctan τ i ω + ∑ k = 1 m 2 arctan 2 ξ k τ k ω 1 − τ k 2 ω 2 − ν π 2 − ∑ j = 1 n 1 arctan τ j ω − ∑ l = 1 m 2 arctan 2 ξ l τ l ω 1 − τ l 2 ω 2 \phi(\omega)=\sum_{i=1}^{m_1}{\arctan\tau_i\omega}+\sum_{k=1}^{m_2}{\arctan{{2\xi_k\tau_k\omega}\over{1-{\tau_k}^2\omega^2}}}-\nu{\pi\over2}-\sum_{j=1}^{n_1}{\arctan\tau_j\omega}-\sum_{l=1}^{m_2}{\arctan{{2\xi_l\tau_l\omega}\over{1-{\tau_l}^2\omega^2}}} ϕ(ω)=i=1∑m1arctanτiω+k=1∑m2arctan1−τk2ω22ξkτkω−ν2π−j=1∑n1arctanτjω−l=1∑m2arctan1−τl2ω22ξlτlω lim ω → 0 ϕ ( ω ) = − ν π 2 , lim ω → ∞ ϕ ( ω ) = − ( n − m ) π 2 \lim_{\omega\rightarrow0}\phi(\omega)=-\nu{\pi\over2},\lim_{\omega\rightarrow\infty}\phi(\omega)=-(n-m){\pi\over2} ω→0limϕ(ω)=−ν2π,ω→∞limϕ(ω)=−(n−m)2π
定义:若 L ( ω c ) = 0 d B L(ω_c)=0dB L(ωc)=0dB,则 ω c ω_c ωc称作剪切频率,也称0dB 频率。剪切频率下的相角为 ϕ ( ω c ) \phi(ω_c) ϕ(ωc)。
5.3.3 最小相位系统、非最小相位系统和开环不稳定系统
1. 最小相位系统
系统传递函数G(s)的零点和极点全部位于s平面的左半部。在具有相同幅频特性的一类系统中,当ω从0变至∞时,最小相位系统的相角变化范围最小。
2. 非最小相位系统
系统传递函数G(s)具有位于s平面右半部的 零点或极点,则这种系统称为非最小相位系统。
3. 开环不稳定系统
系统传递函数G(s)有一个或多个极点落在s平面的右半部,称为开环不稳定系统。
4. 最小相位系统的特点
- 最小相位系统的幅频特性和相频特性是密切相关的。
- 若L(ω)特性的斜率变得更负,则对数相频特性的相位也要朝着更负的方向变化;
- 若L(ω)特性的斜率向正的方向变化,则对数相频特性的相位也将向正的方向变化。
5.4 奈奎斯特稳定判据和系统的相对稳定性
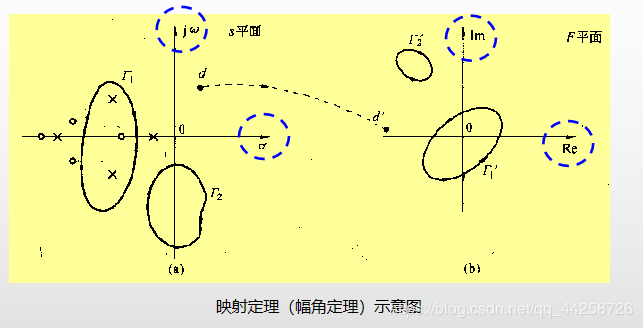
5.4.1 映射定理(幅角定理)
设有一复变函数为 F ( s ) = K 1 ( s − z 1 ) ( s − z 2 ) ⋯ ( s − z m ) ( s − p 1 ) ( s − p 2 ) ⋯ ( s − p n ) F(s)={{K_1(s-z_1)(s-z_2)\cdots(s-z_m)}\over{(s-p_1)(s-p_2)\cdots(s-p_n)}} F(s)=(s−p1)(s−p2)⋯(s−pn)K1(s−z1)(s−z2)⋯(s−zm) 设 s s s平面上不通过 F ( s ) F(s) F(s)任何奇异点的某条封闭曲线Γ,它包围了 F ( s ) F(s) F(s)在 s s s平面上的 Z Z Z个零点和 P P P个极点,当 s s s以顺时针方向沿封闭曲线Γ移动一周时,则在F平面上相对应于封闭曲线Γ的像Γ′将以顺时针的方向围绕原点旋转N圈。 N N N与 Z 、 P Z、P Z、P的关系为 N = Z - P N=Z-P N=Z-P。
5.4.2 奈奎斯特稳定判据(幅角定理)
设系统的开环传递函数为 G ( s ) H ( s ) = K 1 ( s − z 1 ) ( s − z 2 ) ⋯ ( s − z m ) ( s − p 1 ) ( s − p 2 ) ⋯ ( s − p n ) , n ≥ m G(s)H(s)={{K_1(s-z_1)(s-z_2)\cdots(s-z_m)}\over{(s-p_1)(s-p_2)\cdots(s-p_n)}},n\geq m G(s)H(s)=(s−p1)(s−p2)⋯(s−pn)K1(s−z1)(s−z2)⋯(s−zm),n≥m构造辅助函数 F ( s ) = 1 + G ( s ) H ( s ) = 1 + K 1 ( s − z 1 ) ( s − z 2 ) ⋯ ( s − z m ) ( s − p 1 ) ( s − p 2 ) ⋯ ( s − p n ) = ( s − s 1 ) ( s − s 2 ) ⋯ ( s − s n ) ( s − p 1 ) ( s − p 2 ) ⋯ ( s − p n ) F(s)=1+G(s)H(s)=1+{{K_1(s-z_1)(s-z_2)\cdots(s-z_m)}\over{(s-p_1)(s-p_2)\cdots(s-p_n)}}={{(s-s_1)(s-s_2)\cdots(s-s_n)}\over{(s-p_1)(s-p_2)\cdots(s-p_n)}} F(s)=1+G(s)H(s)=1+(s−p1)(s−p2)⋯(s−pn)K1(s−z1)(s−z2)⋯(s−zm)=(s−p1)(s−p2)⋯(s−pn)(s−s1)(s−s2)⋯(s−sn)辅助函数 F ( s ) F(s) F(s)具有以下特点:
- 辅助函数 F ( s ) F(s) F(s)是闭环特征多项式与开环特征多项式之比,其零点和极点分别为闭环极点和开环极点。
- F ( s ) F(s) F(s)的零极点数目相同,都为 n n n。
- F ( s ) F(s) F(s)与开环传递函数 G ( s ) H ( s ) G(s)H(s) G(s)H(s)之间只差一个常量 1 1 1, F ( s ) = 1 + G ( s ) H ( s ) F(s)=1+ G(s)H(s) F(s)=1+G(s)H(s)的几何意义为: F F F平面的坐标原点就是 G H GH GH平面的 ( − 1 , j 0 ) (-1,j0) (−1,j0)点。
构造扩展到整个右平面的封闭曲线 τ \tau τ,该曲线由三段组成: - 正虚轴 s = j ω s=jω s=jω, ω ω ω从 0 0 0变化到 + ∞ +∞ +∞;
- 半径为无限大的右半圆, s = R e j θ s=Re^{jθ} s=Rejθ , R → ∞ R→∞ R→∞, θ θ θ由 π 2 \pi\over2 2π变化到 − π 2 -{\pi\over2} −2π;
- 负虚轴 s = j ω s=jω s=jω, ω ω ω从 − ∞ -∞ −∞变化到 0 0 0。
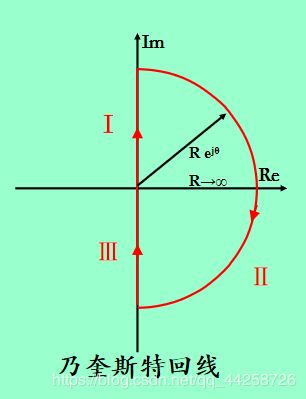
根据映射定理,当s沿着平面上的奈奎斯特回线移动一周时,在 F ( s ) F(s) F(s)平面上的映射曲线将按逆时针方向围绕坐标原点旋转 P − Z P-Z P−Z周。
奈奎斯特稳定判据—闭环控制系统稳定的充分和必要条件:当 ω ω ω从 − ∞ -∞ −∞变化到 + ∞ +∞ +∞时,系统的开环频率特性 G ( j ω ) H ( j ω ) G(jω)H(jω) G(jω)H(jω)按逆时针方向包围 ( − 1 , j 0 ) (-1,j0) (−1,j0)点 P P P周, P P P为位于 s s s平面右半部的开环极点的数目。
若开环系统是稳定的,即位于 s s s平面右半部的开环极点的数目为零,则闭环控制系统稳定的充分和必要条件是:当 ω ω ω从 − ∞ -∞ −∞变化到 + ∞ +∞ +∞时,系统的开环频率特性不包含 ( − 1 , j 0 ) (-1,j0) (−1,j0)点。
5.4.3 奈奎斯特在 I 型和 II 型系统中的应用
按照幅角定理的规定,在 s s s平面的奈氏回线不能通过 F ( s ) F(s) F(s)的奇异点。 重新定义乃氏回线如下:
- 正虚轴 s = j ω s=jω s=jω, ω ω ω从 0 + 0^+ 0+变化到 + ∞ +∞ +∞;
- 半径为无限大的右半圆, s = R e j θ s= Re^{jθ} s=Rejθ, R → ∞ R→∞ R→∞, θ θ θ由 π / 2 π/2 π/2变化到 − π / 2 -π/2 −π/2。
- 负虚轴 s = j ω s=jω s=jω, ω ω ω从$-∞4变化到 0 − 0^- 0−;
- 半径为无穷小的右半圆, s = ε e j θ s= εe^{jθ} s=εejθ, ε → 0 ε→0 ε→0, θ θ θ由 − π / 2 -π/2 −π/2变化到 π / 2 π/2 π/2。


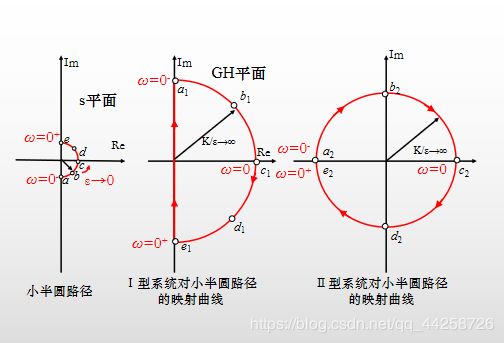
随着 ω ω ω的增大,若频率特性曲线 G H ( j ω ) GH (jω) GH(jω)以逆时针方向包围 ( − 1 , j 0 ) (-1,j0) (−1,j0)点一圈,则 G H ( j ω ) GH(jω) GH(jω)曲线的正半段必然从上至下穿过 G ( s ) G(s) G(s)平面负实轴的 ( − ∞ , − 1 ) (-∞,-1) (−∞,−1)区段一次。这种穿越伴随着相角的增加而穿越的,故称为正穿越。反之叫负穿越。 N = 2 ( N + − N − ) = P − Z N=2(N^+-N^-)=P-Z N=2(N+−N−)=P−Z
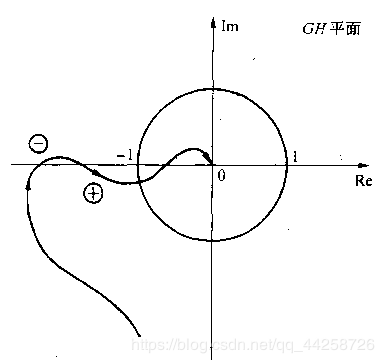
5.4.4 根据伯德图判别系统的稳定性
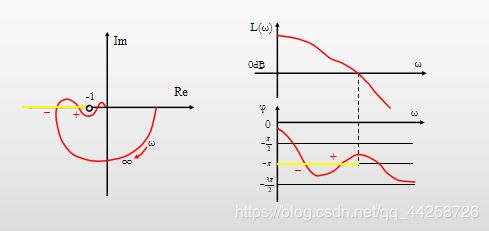
采用伯德图时乃奎斯特判据的表述如下:
闭环系统稳定的充要条件是:当 ω ω ω从 0 0 0变化到 + ∞ +∞ +∞时,在开环对数幅频特性 L ( ω ) ≥ 0 L(ω)≥0 L(ω)≥0的频段内,相频特性 φ ( ω ) φ(ω) φ(ω)穿越 − π -π −π线的次数(正穿越和负穿越之差)为 P / 2 P/2 P/2。 P P P为 s s s平面右半部开环极点的数目。
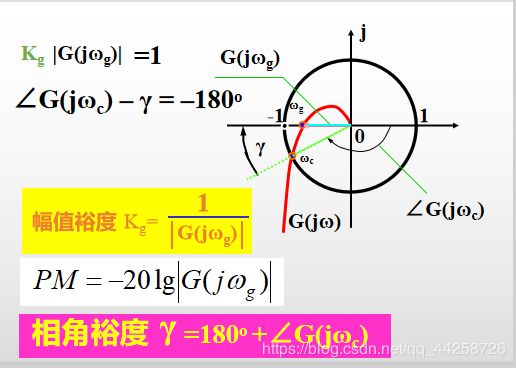
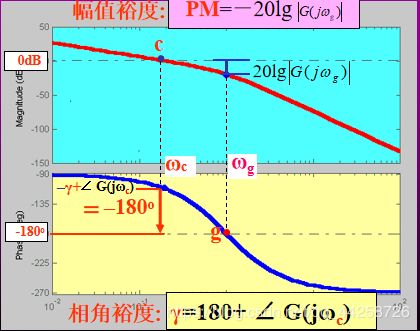
5.4.5 系统的相对稳定性和稳定裕度
幅值裕度 K g = 1 ∣ G ( j ω g ) ∣ , 其 中 K_g={1\over|G(j\omega_g)|},其中 Kg=∣G(jωg)∣1,其中
相角裕度 γ = 18 0 。 + ∠ G ( j ω c ) , 其 中 \gamma=180^。+ \angle G(j\omega_c),其中 γ=180。+∠G(jωc),其中
5.5 利用开环频率特性分析系统性能
5.5.1 L ( ω ) L(\omega) L(ω)低频渐近线与系统稳态误差之间的关系
- 开环传递函数中积分环节的数目(系统的型别)决定了低频渐近线的斜率。
- 低频渐近线的高度决定了开环传递系数(稳态误差系数)。
1. 0型系统 G ( j ω ) = K j ω T + 1 G(j\omega)={K\over{j\omega T+1}} G(jω)=jωT+1K则低频渐近线为 L ( ω ) = 20 l g K L(\omega)=20lgK L(ω)=20lgK

2. I型系统 G ( j ω ) = K j ω ( j ω T + 1 ) G(j\omega)={K\over j\omega({j\omega T+1})} G(jω)=jω(jωT+1)K则低频渐近线为 L ( ω ) = 20 l g K ω = 20 l g K − 20 l g ω L(\omega)=20lg{K\over\omega}=20lgK-20lg\omega L(ω)=20lgωK=20lgK−20lgω

3. II型系统 G ( j ω ) = K ( j ω ) 2 ( j ω T + 1 ) G(j\omega)={K\over (j\omega)^2({j\omega T+1})} G(jω)=(jω)2(jωT+1)K则低频渐近线为 L ( ω ) = 20 l g K ω 2 = 20 l g K − 20 l g ω 2 L(\omega)=20lg{K\over\omega^2}=20lgK-20lg\omega^2 L(ω)=20lgω2K=20lgK−20lgω2
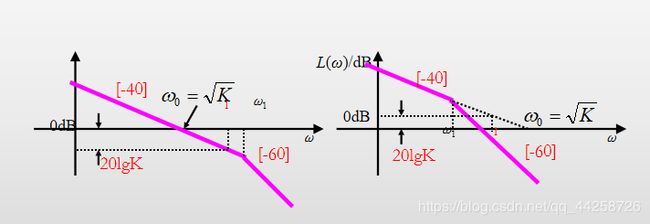
5.5.2 L ( ω ) L(\omega) L(ω)中频斜率与系统稳定性之间的关系
中频段:剪切频率 ω c ω_c ωc附近的频率段。
在 ω c ω_c ωc处,$ L(ω)$曲线的斜率对相角裕度 γ \gamma γ 的影响最大,远离 ω c ω_c ωc处的对数幅频特性对 γ \gamma γ 的影响很小。

(1)若 ω c 、 ω 2 \omega_c、\omega_2 ωc、ω2不变, ω 1 ↓ \omega_1\downarrow ω1↓, γ ↑ \gamma\uparrow γ↑; ω 1 ↑ \omega_1\uparrow ω1↑, γ ↓ \gamma\downarrow γ↓
(2)若 ω c 、 ω 1 \omega_c、\omega_1 ωc、ω1不变, ω 2 ↓ \omega_2\downarrow ω2↓, γ ↓ \gamma\downarrow γ↓; ω 2 ↑ \omega_2\uparrow ω2↑, γ ↑ \gamma\uparrow γ↑

(3) 若 ω 1 、 ω 2 ω1、ω2 ω1、ω2不变, 令 ω 2 = h × ω 1 ω2=h\timesω1 ω2=h×ω1 , h表示中频段的宽度
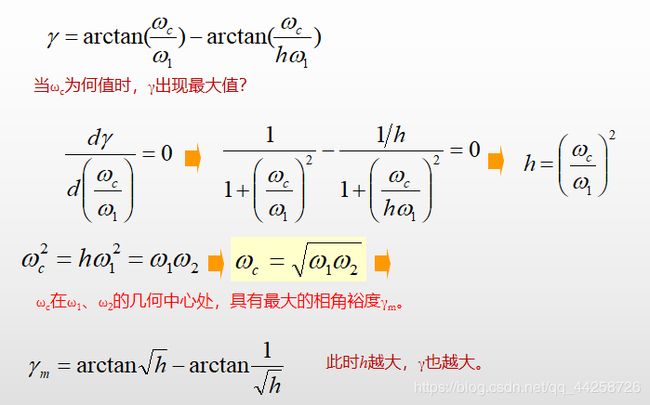
中频段的宽度越大, γ \gamma γ 越大。
5.5.3 开环频率特性和系统动态性能的关系
开环频率特性的特征量(开环频域指标): γ 和 ω c \gamma 和\omega_c γ和ωc
系统动态性能的时域指标: σ % 、 t s \sigma{\%}、t_s σ%、ts
1. 二阶系统
闭环传函为 ω n 2 s 2 + 2 ζ ω n s + ω n 2 {\omega_n}^2\over{s^2+2\zeta\omega_ns+{\omega_n}^2} s2+2ζωns+ωn2ωn2
开环传函为 G ( s ) = ω n 2 s ( s + 2 ζ ω n ) G(s)={{\omega_n}^2\over{s(s+2\zeta\omega_n)}} G(s)=s(s+2ζωn)ωn2
开环频率特性为 G ( j ω ) = ω n 2 j ω ( j ω + 2 ζ ω n ) G(j\omega)={{\omega_n}^2\over{j\omega(j\omega+2\zeta\omega_n)}} G(jω)=jω(jω+2ζωn)ωn2
(1) γ \gamma γ和 σ % \sigma{\%} σ%的关系
γ \gamma γ越小(即 ζ \zeta ζ越小) σ % \sigma\% σ%越大; γ \gamma γ越大, σ % \sigma\% σ%就越小 通常为了使二阶系统在阶跃函数的作用下振荡不至于过于剧烈,以及调节时间不至太长,通常取 30 ° < γ < 60 ° 30°<γ<60° 30°<γ<60°。
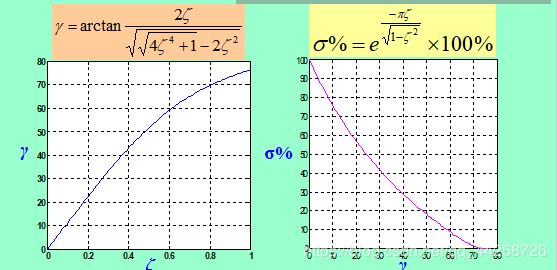
(2) γ \gamma γ、 ω c \omega_c ωc与 t s t_s ts的关系
t s ω c = 6 tan γ t_s\omega_c={6\over{\tan\gamma}} tsωc=tanγ6
- 调节时间 t s t_s ts与 γ \gamma γ和 ω c ω_c ωc都有关。如果相角裕度 γ \gamma γ已经给定,那么 t s t_s ts与 ω c ω_c ωc成反比。
- 如果两个二阶系统的相角余量 γ \gamma γ相同,那么它的最大超调量也相同,则 ω c ω_c ωc较大的系统,其调节时间 t s t_s ts必然较短。
2. 高阶系统
一般三阶或三阶以上的系统要导出其频域特征量和时域指标的关系比较困难,可用近似方法。 σ % = [ 0.16 + 0.4 ( 1 sin γ − 1 ) ] × 100 % \sigma{\%}=[0.16+0.4({1\over{\sin\gamma}}-1)]\times100\% σ%=[0.16+0.4(sinγ1−1)]×100% t s = π ω c [ 2 + 1.5 ( 1 sin γ − 1 ) + 2.5 ( 1 sin γ − 1 ) 2 ] t_s={\pi\over\omega_c}[2+1.5({1\over{\sin\gamma}}-1)+2.5({1\over{\sin\gamma}}-1)^2] ts=ωcπ[2+1.5(sinγ1−1)+2.5(sinγ1−1)2] 3 5 。 < γ < 9 0 。 35^。<\gamma<90^。 35。<γ<90。

随着 γ \gamma γ值的增加,超调量和调整时间都明显下降。
5.5.4 L ( ω ) L(\omega) L(ω)高频段对系统性能的影响
若 L ( ω ) L(ω) L(ω)的高频段特性是由小时间常数的环节构成,其转折频率均远离截止频率 ω c ω_c ωc,则对系统的动态响应影响不大。
L ( ω ) L(ω) L(ω)特性高频段的幅值,反映出系统对输入端高频信号的抑制能力,高频段的分贝值越低,说明系统对高频信号的衰减作用越大,即系统的抗干扰能力越强。
希望得到的开环对数幅频特性应具有如下的性质:
- 为保证系统的稳态精度,低频段应有较高的分贝值。 如果要求具有一阶或二阶无差度(阶跃或斜坡输入信号的响应无误差).则 L ( ω ) L(ω) L(ω)特性的低频段应具有 − 20 d B / d e c -20 dB/dec −20dB/dec或 − 40 d B / d e c -40 dB/dec −40dB/dec的斜率( I 型或 II 型)。
- L ( ω ) L(ω) L(ω)应以 − 20 d B / d e c -20dB/dec −20dB/dec的斜率穿过零分贝线,且具有一定的中频段宽度。这样系统就有足够的稳定裕度,以保证闭环系统具有较好的平稳性。
- L ( ω ) L(ω) L(ω)特性应具有尽可能高的截止频率 ω c ω_c ωc,以提高闭环系统的快速性。
- L ( ω ) L(ω) L(ω)的高频段应有较大的斜率,以增强系统的抗干扰能力。
5.6 利用开环频率特性分析系统性能
5.6.1 闭环频率特性的几个性能指标
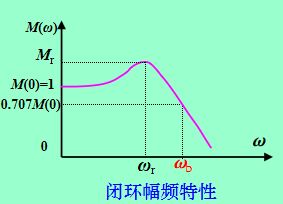
1. 直流增益(零频振幅比) M ( 0 ) M(0) M(0)
直接反映了系统的稳态精度。 M ( 0 ) M(0) M(0)越接近于1,表示系统的稳态误差越小。
2. 谐振峰值 M r Mr Mr
表明系统对某个频率的正弦信号反应强烈,有谐振的趋势,反映系统的相对稳定性和阶跃响应超调量。
3. 谐振频率 ω r ω_r ωr
ω r ω_r ωr较高时, t p t_p tp值可能较小。
4.频带宽度(截止频率) ω b ω_b ωb
指衰减到0.707M(0)所对应的频率,也叫通频带
带宽较宽,表明系统能通过较高频率的输入信号,通频带较宽的系统一方面复现输入信号的能力较强,另一方面抑制输入端高频干扰的能力较弱。带宽和调节时间也有着密切的关系, ω b ω_b ωb越大,调节时间越短。
5.6.2 闭环频域指标和时域指标的关系
闭环系统的频域指标:谐振峰值 M r M_r Mr和频带宽度 ω b ω_b ωb
闭环系统的时域指标:超调量 σ % \sigma\% σ%和调整时间 t s t_s ts
二阶系统 Φ ( s ) = ω n 2 s 2 + 2 ζ ω n s + ω n 2 \Phi(s)={{\omega_n}^2\over{s^2+2\zeta\omega_ns+{\omega_n}^2}} Φ(s)=s2+2ζωns+ωn2ωn2 G ( s ) = ω n 2 s ( s + 2 ζ ω n ) , ( 0 < ζ < 1 ) G(s)={{\omega_n}^2\over{s(s+2\zeta\omega_n)}},(0<\zeta<1) G(s)=s(s+2ζωn)ωn2,(0<ζ<1)
闭环系统的频率特性为 Φ ( j ω ) = ω n 2 ( ω n 2 − ω 2 ) + j 2 ζ ω n ω \Phi(j\omega)={{\omega_n}^2\over{({\omega_n}^2-\omega^2)+j2\zeta\omega_n\omega}} Φ(jω)=(ωn2−ω2)+j2ζωnωωn2
(1) M r M_r Mr和 σ % \sigma\% σ%的关系 M r = 1 2 ζ 1 − ζ 2 , 0 ≤ ζ ≤ 0.707 M_r={1\over{2\zeta\sqrt{1-\zeta^2}}},0\leq\zeta\leq0.707 Mr=2ζ1−ζ21,0≤ζ≤0.707
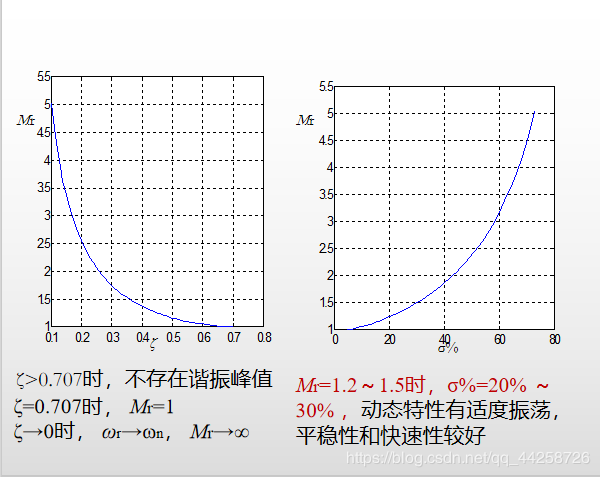
(2) M r M_r Mr、 ω b \omega_b ωb与 t s t_s ts的关系 ω b = ω n 1 − 2 ζ 2 + 2 − 4 ζ 2 + 4 ζ 4 \omega_b=\omega_n\sqrt{1-2\zeta^2+\sqrt{2-4\zeta^2+4\zeta^4}} ωb=ωn1−2ζ2+2−4ζ2+4ζ4 ω b t s = 3 ζ 1 − 2 ζ 2 + 2 − 4 ζ 2 + 4 ζ 4 \omega_bt_s={3\over\zeta}\sqrt{1-2\zeta^2+\sqrt{2-4\zeta^2+4\zeta^4}} ωbts=ζ31−2ζ2+2−4ζ2+4ζ4
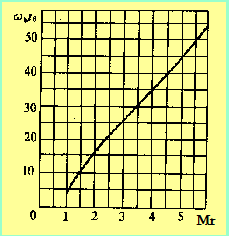 对于给定的谐振峰值 M r M_r Mr,调节时间 t s t_s ts与带宽 ω b ω_b ωb成反比,频带宽度越大则调节时间越短。
对于给定的谐振峰值 M r M_r Mr,调节时间 t s t_s ts与带宽 ω b ω_b ωb成反比,频带宽度越大则调节时间越短。
本章小结
- 频域分析法可以根据系统开环频率特性判断闭环系统的性能,并能较方便地分析系统参量对时域响应的影响,从而指出改善系统性能的途径。
- 传递函数的极点和零点均在 s s s左边平面的系统称为最小相位系统。这类系统的幅频特性和相频特性有唯一的对应关系,根据对数幅频特性曲线就能写出系统的传函。
- 奈氏稳定判据是根据开环频率特性曲线逆时针围绕 ( − 1 , j 0 ) (-1, j0) (−1,j0)点的情况(即 N N N等于多少)和开环传函在 s s s右半平面的极点数 P P P来判断闭环系统的稳定性。
- 考虑系统内部参数和外界环境变化的影响,要求系统应有足够的稳定裕度,通常用相位裕度 γ \gamma γ和增益裕度 K g K_g Kg(或 G M GM GM)来表示。