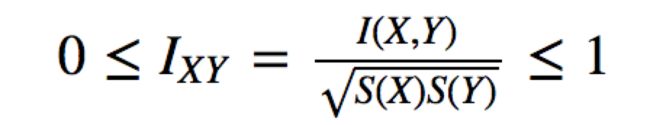群体遗传学数学基础
群体遗传学数学基础
- 数学基础
- 一对等位基因孟德尔群体及其数量表示
- 1.群体遗传结构
- 2.基因频率由基因型频率唯一确定
- 3.哈温伯格定律
- 4.平衡群体的性质
- 4.1 Shannon信息熵最大
- 4.2 S(G)=2S(A)
- 遗传多态性
- 1.描述遗传多态性
- 2.杂合度H，群体基因的多样度
- 总结
- 群体中亲属关系研究
- 1. 有限个状态（值）的二维离散型随机变量的联合分布
- 2. 当X和Y为数量性变量
- 3. 当X和Y不能量化
- 4. 近交系数F
- 系统树重建
- 1. 群体遗传分化的度量
- 1.1 Fst
- 1.2 Nei标准距离D
- 设孟德尔群体为复等位基因群体
- 群体内纯合基因型比例J和杂合基因型比例H：
- 平均密码子差数(codon differences)
- Nei标准距离
- 2. 建树方法
- 2.1 距离法
- UPGMA法（类平均法）
- 邻接法
- 2.2 简约法（MP）
- 2.3 最大似然法（ML）
- 比较总结
- 其他参考
数学基础
以下全明白才能看懂之后的：
- 排列组合
- 数学期望方差
- 求导
- 离散型二维随机变量
- 信息熵
- 拉格朗日乘子法
- 拉格朗日函数构造
一对等位基因孟德尔群体及其数量表示
- 孟德尔群体：群体遗传学研究对象，是能够互交繁殖的个体集合
- 孟德尔群体的遗传结构：它的基因分布和基因型分布
1.群体遗传结构
(AA,Aa,aa)=(p2,p1,p0)
(A,a)=(p,q)
2.基因频率由基因型频率唯一确定
p=p2+1/2p1
q=p0+1/2p1
3.哈温伯格定律
在随机交配的大孟德尔群体中，其遗传结构为
(AA,Aa,aa)=(p2,2pq,q2)
(A,a)=(p,q)
随机交配下的平衡：
4.平衡群体的性质
4.1 Shannon信息熵最大
平衡群体：
(AA,aA,Aa,aa)=(p2,pq,pq,q2)
由基因库行程的基因型（正反交分开）信息源：
G =
[AA Aa aA aa
p11 p12 p21 p22]
由pij计算基因A，a的频率p，q ：
基因型的信息熵：
使s(G)最大的基因型频率可归结为如下条件极值：
https://www.numberempire.com/latexequationeditor.php
\begin{cases}
\sum\limits_{i=1}^2\sum\limits_{j=1}^2(p_{ij})=1 \\
p=1/2\sum\limits_{j=1}^2(p_{1j}+p_{j1}) \\
q=1/2\sum\limits_{j=1}^2(p_{2j}+p_{j2}) \\
s(G)=-\sum\limits_{i=1}^2\sum\limits_{j=1}^2(p_{ij}lnp_{ij})=max
\end{cases} \
构建拉格朗日函数约束条件求解：
p11=p2
p22=q2
p12=p21=pq
4.2 S(G)=2S(A)
基因库(A,a)=(p,q)的信息熵：
S(A)=-(plnp+qlnq), 0<=S(A)<=ln2
基因型的信息熵：
S(G)=-(p2lnp2+2pqlnpq+q2lnq2) =-2(plnp+qlnq)=2S(A)
遗传多态性
1.描述遗传多态性
- 对于群体的遗传变异，通常用多态位点的比例来度量
- 群体中基因型的多型性，通过群体中两性配子随机结合成各种基因型中杂合体的比例来描述，称为杂合度
多态位点：基因分布中绝大多数等位基因的频率在区间(0.01,0.99)之内，比如ABO血型位点
2.杂合度H，群体基因的多样度
纯合度J，群体基因的一致度
J不是遗传多态性的指标
J = 1-H
0\leq H= 1-\sum\limits_{i=1}^k(p_{i}^2 )\leq\frac{k-1}{k} \\
\frac{1}{k}\le J=\sum\limits_{i=1}^k(p_{i}^2)\le1
位点中的有效基因数：
1/J
总结
- H和J是位点中基因个数和它们出现频率的综合指标
- 对于一个群体来说，H越大，说明基因型类型越多，对适应不同的环境越有利，有更大的进化潜力
- H是描述基因变异的度量，和统计中的方差概念不同
群体中亲属关系研究
在群体遗传学研究中，群体中的个体间有亲子关系、同胞关系等亲属关系，这些数量关联性分析可以归结为具有有限个状态（值）的二维离散型随机变量的分析和计算。
1. 有限个状态（值）的二维离散型随机变量的联合分布
| X \ Y | y1 | y2 | … | yn | sum |
|---|---|---|---|---|---|
| x1 | p11 | p12 | … | p1n | p1. |
| x2 | p21 | p22 | … | p2n | p2. |
| … | … | … | … | … | … |
| xm | pm1 | pm2 | … | pmn | pm. |
| sum | p.1 | p.2 | … | p.n | 1 |
Y的分布：
(y1,y2,…,yn)=(p.1,p.2,…p.n)
称为联合分布XY中关于Y的边缘分布
X的分布：
(x1,x2,…,xm)=(p1.,p2.,…pm.)
称为联合分布XY中关于X的边缘分布
利用二维分布可以表征X与Y间的关联程度:
- 相关系数rXY
- 关联系数IXY
2. 当X和Y为数量性变量
X的均值与方差：
Y的均值与方差：
X与Y的协方差Cov(X,Y)与相关系数rXY:
- Cov(X,Y)表征X与Y的协同变异度
- rXY表征X与Y线性相关的程度|rXY|<=1
\begin{cases}
\mu_{X}=\sum\limits_{i=1}^m(x_{i}p_{i.})\\
\delta_{X}^2=\sum\limits_{i=1}^m(x_{i}^2p_{i.})-\mu_{X}^2
\end{cases} \\
\begin{cases}
\mu_{Y}=\sum\limits_{j=1}^n(y_{j}p_{.j})\\
\delta_{Y}^2=\sum\limits_{j=1}^n(y_{j}^2p_{.j})-\mu_{Y}^2
\end{cases} \\
\begin{cases}
Cov(X,Y)=\sum\limits_{i=1}^m\sum\limits_{j=1}^n(x_{i}y_{j}p_{ij})-\mu_{X}\mu_{Y}\\
r_{XY}=\frac{Cov(X,Y)}{\delta_{X}\delta_{Y}}
\end{cases} \\
3. 当X和Y不能量化
如果X和Y不能量化，可以把联合分布XY视为联合信源，通过计算X、Y和联合分布XY的shannon信息熵S(X)、S(Y)、S(XY)，表征出X与Y间的互信息I(X,Y)，它是X与Y间的由关联所引起的信息量表达。
X,Y和XY的信息熵：
X与Y的互信息量：
I(X,Y)=S(X)+S(Y)-S(XY)
当X与Y相互独立时：
pij=pi.+p.j
S(XY)=S(X)+S(Y), I(x,y)=0
X与Y的信息关联系数IXY:
4. 近交系数F
- 当存在一定程度的近交，在产生下一代时，形成的纯合子（AA和aa）的比例比配子随机结合的概率大，反之杂合子偏小
- 配子间的相关系数r或信息关联系数I为近交系数F
系统树重建
1. 群体遗传分化的度量
1.1 Fst
- 用于衡量种群分化程度，取值从0到1，分化指数越大，差异越大
- 为0则认为两个种群间是随机交配的，基因型完全相似；为1则表示是完全隔离的，完全不相似
- 从基因的多样性来估计，比如SNP或者microsatellites(串联重复序列一种，长度小于等于10bp)，适用于亚群体间多样性的比较
- 是一种以哈温平衡为前提的种群遗传学统计方法
Fst的计算原理与实战
Fst详解（具体计算步骤）
1.2 Nei标准距离D
设孟德尔群体为复等位基因群体
- 其基因频率分布为：(A1,A2,…,Ak)=(p1,p2,…,pk)
- 其中pi为基因Ai的频率，pi求和为1
- 群体的基因型，若正反交分开有k2个；若正反交不分开有k(k+1)/2个
- 群体平衡时，基因型AiAi的频率为pi2，基因型AiAj=AjAi=pipj
群体内纯合基因型比例J和杂合基因型比例H：
平均密码子差数(codon differences)
对于随机交配群体来说，如果位点中每个基因均由m个独立的密码组成，随机抽取两个等位基因，它们在第i个密码子上不同的概率为：
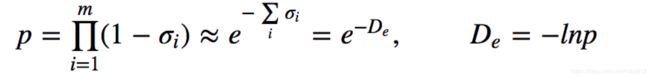
- 其中De为每个位点的期望密码子差数
- 由于不同等位基因间至少有一个密码子差数，因而位点的平均密码子差数Dx就可以表示基因多样度
- 群体中基因一致度为J，它是群体中纯合体的频率，若p=J，则De=-lnJ.显然De是Dx的偏低估计，因为除微生物外，一个基因上的密码子是紧密连锁并不独立的，即J比p要大一些
0<=Dx=-lnJ<=lnk (k为位点的基因个数)
- Nei建议，如果测定了r个位点，可以用各位点纯合度的几何平均值代替上式中的J，得到平均密码子差异D’x
p=\prod\limits_{i=1}^m(1-\sigma_{i}) \approx e^{-\sum\limits_{i}\sigma_{i}}=e^{-D_{e}},\qquad D_{e}=-lnp\\
0\le D'_{x}=-ln^r\sqrt{J_{1}J_{2}...J_{r}} \le lnk
Nei标准距离
设亚群x和y只检测了一个位点，基因频率分布分别为(x1,x2,…,xk)和(y1,y2,…,yk)，则从x，y及x与y中随机选出两个基因相同的概率为：
x和y的Nei相似指数为：
（在数学上，它是向量x和y夹角a的余弦值，即IN=cosa）
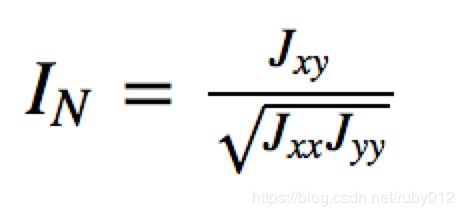
Nei标准遗传距离：
是x与y的密码子差数的偏低估计
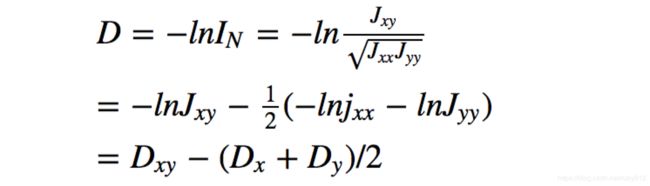Dx=-lnJxx x的密码子差数（未正规化）
Dy=-lnJyy y的密码子差数（未正规化）
Dxy=-lnJxy x与y的密码子差数（未正规化）
当测定是多位点时：
J’xx J’yy J’xy是各位点的Jxx Jyy Jxy的几何平均值
D’比单位点更好
2. 建树方法
2.1 距离法
对于m个分类群，通过分子特征的加工可以得到一个对称的距离矩阵（m阶方阵），例如包括4个分类群的距离矩阵为：
| OTU1 | 0 | 0.15 | 0.20 | 0.35 |
|---|---|---|---|---|
| OTU2 | 0 | 0.18 | 0.28 | |
| OTU3 | 0 | 0.22 | ||
| OTU4 | 0 |
UPGMA法（类平均法）
系统聚类法的一种，在上述矩阵中，首先将OTU1和OTU2聚成新类OTUr（其距离最短0.15），将原来4个分类群变成新的3个分类群，重新计算距离矩阵
设在某一聚类步骤j中，将OTUp（内含np个原始分类群）、OTUq（内含nq个原始分类群）并为新类OTUrj，所谓UPGMA法，是指这一步骤中任一新类OTUi与OTUrj的距离用类平均法计算，公式为：
邻接法
在谱系树上，如果两个分类群间通过一个内结点相连，那么称它们为“近邻”
原理：逐步寻找新的近邻，使最终生成的分支数总长度最小，其中距离计算仍然按照类平均法
2.2 简约法（MP）
对于分子谱系树来讲，核苷酸／氨基酸总替代数最小的拓扑结构树就是最大简约树
步骤：
- 确定所有的信息位点
- 对所有可能的树形，计算每个信息位点上发生核苷酸替代的最低次数，并对所有信息微店的最低替代数目求和
- 选择核苷酸替代总数最小的树作为最大简约谱系树
一般来说，如果序列分化程度较低，核苷酸替代速率恒定，序列长度较大的情况下，最大简约法优于距离矩阵法
2.3 最大似然法（ML）
基本原理：对每个谱系拓扑结构，找到符合最大似然值最高的谱系拓扑结构作为重建谱系树
比较总结
距离矩阵法：
- 前提是进化速率相等，但实际并不是这样，因而常用的距离都用一定的转换来校正
- 当序列较短时，较易出错
- 在运算时间上，只有距离矩阵法最省
最大简约法：
- 没有明确的假设前提，但其“最小核苷酸替代数目“原则意味着要求平行、趋同和回复替代最少
- 因此进化速率差异很大或序列间分化度较大时，效果不好
最大似然法：
- 所用替代数学模型对速率假定并不敏感，但计算复杂
计算机模拟研究比较：
- 在进化速率恒定情况下，最大简约法不如邻接法，最大似然法取决于替代数学模型
- 在进化速率可变情况下，最大简约法不如转换矩阵法和邻接法，最大似然法最优
- 如果转换频率大大高于颠换时，邻接法要优于最大似然法
转换（Transitions）：A <–>G or C<–>T
颠换（Transversions）：其他
转换(transitions)和颠换(transversions)
其他参考
群体遗传学基础概念
最大信息熵原理与群体遗传平衡
群体遗传分析—LD连锁不平衡
群体遗传学—浅谈基因流
一文读懂进化树