svm随机次梯度下降算法-pegasos

基本思想

使用随机梯度下降直接解SVM的原始问题。

摘要

本文研究和分析了基于随机梯度下降的SVM优化算法，简单且高效。（Ο是渐进上界，Ω是渐进下界）本文证明为获得一定准确率精度 ϵ 所需的迭代次数满足 O(1ϵ) ，且每一次迭代都只使用一个训练样本。相比之下，以前分析的SVM随机梯度下降次数满足 Ω(1ϵ2) 。以前设计的SVM中，迭代次数也与 1λ 线性相关 。对于线性核，pegasos算法的总运行时间是 O(dϵλ) ,其中d是每一个样本中非零特征在边界上的个数。因此，运行时间和训练集的大小不是直接相关的，那么本算法尤其适合大规模的数据集。本文算法也可以拓展到非线性核上，但只能基于原始的目标函数，此时的运行时间和数据集大小线性相关 O(mϵλ) 。本文算法尤其适用于大规模文本分类问题，比之前的SVM加速了几个数量级。

引言

SVM是一种高效流行的分类器、SVM是一种典型的受限二次规划问题。然而，基于基本形式，SVM实际上是一个附带惩罚因子的无限制经验损失最小化问题。
定义目标函数为

f(ω)=minwλ2||ω||2+1m∑l(ω,(x,y))

其中：

l(ω,(x,y))=max{0,1−y<ω,x>}

使用随机梯度下降解目标函数的算法称作pegasos。在每一次的迭代中，随机挑选一个训练样本计算目标函数的梯度，然后在在相反的方向走一个预订好的步长。根据上述算法，整体算法的运行时间满足 O(nλϵ) ,其中n是w和x的维度。算法可以进一步优化为 O(dϵλ) ,其中d是每一个样本中非零特征在边界上的个数。pegasos只与算法的随机步骤有关，和数据集无关。

1. Interior Point (IP) methods：可以使用拟牛顿法对目标函数进行优化，但算法因为使用了如海森矩阵等便需 m2 的空间复杂度， 其中m是样本数。
2. Decomposition methods: 使用类似SMO的算法解SVM的对偶优化问题，但是这会导致相对比较慢的收敛速率。
3. Primal optimization:SVM大部分的求解方法都在解决对偶问题，尤其是在非线性核问题上。因为，即使SVM使用了非线性核，我们也可以将 ω 替换为 ∑αiyixi ，从而将解决原目标函数的受约束优化问题转化为没有约束条件的优化问题。其实，直接解决原问题也有人研究过，比如使用smooth loss functions代替 hinge loss，这样将问题变成一个平滑的不受限制的优化问题，然后使用梯度下降和牛顿法来求解。本文采取了类似方法，针对hinge loss的不可微性，直接使用sub-gradients（子梯度）代替梯度。
4. 尽管随机梯度下降算法是最差的优化算法，但是可以产生最好的泛化性能。
5. 有一种基于随机子梯度下降的算法和pegasos比较类似，但是其非常重要的一部分是学习步长的设置，收敛速率最坏的上界是 Ω(1(λϵ)2) 。欧几里得距离的平方可以被优化到0，但是收敛速率决定于步长参数的设置。pegasos调参简单。
6. online methods：在线学习算法一般与随机梯度下降算法结合，如每一次迭代只使用一个样本。在线学习算法被提出为SVM的快速替代方案。在线算法可以使用在线到批量转换方案来获得具有低泛化误差的预测器，但是这种方法不一定能够解决原问题的 ϵ 精度要求，并且它们的性能通常低于直接批量优化器。如上所述，Pegasos共享了在线学习算法的简单性和速度，但它保证融合到最优的SVM解决方案。

pegasos 算法

基于上述提到的方法，pegasos在原始目标函数上通过精致挑选的步长使用随机梯度下降求解。将在本部分详细描述pegasos的过程并提供伪代码。同时也阐述基本算法的一系列变种，并讨论几个实际问题。

基本算法

随机选取一个训练样本 it 其中i代表选取的样本，t代表迭代的次数，带入

f(ω)=minwλ2||ω||2+1m∑l(ω,(x,y))

得到近似的目标函数：

f(ω,it)=λ2||ω||2+l(ω,(xit,yit))

计算次梯度得：

∇t=λωt−I[yit{ωt,xit}<1]yitxit

其中， I[yit{ωt,xit}<1] 是指示函数，如果是真则值为1，反之为0 。

伪代码如下：

输入数据集S,正则化因子 λ ，迭代次数T,则每一次迭代式为：

ωt+1<=ωt−ηt∇t

ηt=1λt 是变动步长，和学习率 λ 成反比，随着迭代次数t的增加而减少。联合 ∇t=λωt−I[yit{ωt,xit}<1]yitxit 展开迭代式得：

ωt+1<=ωt−ηt[λωt−I[yit{ωt,xit}<1]yitxit]

进一步推倒得：

ωt+1<=(1−1t)ωt+ηtI[yit{ωt,xit}<1]yitxit]

如果指示函数为真，则：

ωt+1<=(1−1t)ωt+ηtyitxit

如果为假，则

ωt+1<=(1−1t)ωt

迭代T后，输出 ωt+1

类似的mini-batch pegasos算法伪代码如下：

稀疏特征

当训练集样本是稀疏的时候，可以把 ω 表示成向量v 和标量a相乘。 ω=av 。那么容易证明每一次迭代的计算运行次数O(d)，d是非零元素的个数。

核函数解决非线性分类问题

SVM的主要优势是可以使用核方法直接在特征空间分类。可以如此做关键是表示定理（ Representer Theorem ），根据表示定理可以通过训练数据的线性组合求得原目标函数的最优解。即在训练SVM的时候可以不直接使用训练数据，通过指定核操作的训练数据的内积结果训练。也就是说，不考虑训练样本x本身的线性函数的预测变量，我们考虑训练样本的隐式映射φ（x）后的线性函数的预测变量。
推导过程如下：
如求解线性不可分的 f(ω) ,将x映射到特征空间：

f(ω)=minwλ2||ω||2+1m∑(x,y)∈Sl(ω;(ϕ(x),y))

其中：

l(ω;(ϕ(x),y))=max{0,1−y<ω,ϕ(x)>}

为使用核函数将内积 <ω,ϕ(x)> 映射到特征空间的内积，将 ω 用x来表示，通过对原目标函数求次梯度可以得到：

ωt+1=(1−1t)ωt+ηtI[yit{ωt,ϕ(xit)}<1]yitϕ(xit)

设：

vt=I[yit{ωt,ϕ(xit)}<1]yitϕ(xit)

则迭代式重写为：

ωt+1=(1−1t)ωt+ηtvt

根据迭代式的递推可得：

ωt+1=(t−1t)ωt+ηtvt

ωt+1=1λt∑i=1tvt

ωt+1=1λt∑i=1tI[yit{ωt,ϕ(xit)}<1]yitϕ(xit)

设 αt+1[j] 为第t+1次，样本j被选中且损失不为0的次数（指示函数为1）。
则：

ωt+1=1λt∑j=1mαt+1[j]yitϕ(xit)

带回到 l(ω) ，通过T次随机次梯度下降伪代码如下：

根据输出 αT+1 得到 ω
映射φ（·）并不明确指定，而是训练样本通过映射φ（·）之后通过核计算K（x，x’）=φ（x），φ（x’）得到内积结果。本文中，无需将目标函数转换为对偶函数，直接最小化原始问题，同时仍然使用核方法。Pegasos算法可以仅使用内核来实现求解，而不需要直接访问特征向量 ϕ（x） 或显式访问权重向量 ω
因为需要遍历m个样本，故时间复杂度为 O(mϵλ)

结合偏置项b

当正负样本比例不均衡的时候，偏置项比较重要。
在算法的外部加一层找寻b的外循环，即对于不同的b值，均使用pegasos求解出各自的 ω 。优化问题是 minωλ2||w||2+J(b;S) 目标函数如下：

J(b;S)=minω1m∑l((ω,b);(x,y))

J(b;S)=minω1m∑(x,y)∈S[1−y(<ω,x>+b)]+

因为b是固定值，在内层循环求解时，仍然可以使用pegasos算法,且这种方法的时间复杂度仍然保持在 O(dϵλ)

实验比对

pegasos算法与SDCA,SVM_LIGHT,LASVM比较

线性核

第一行是原目标函数的收敛曲线，第二行是分类误差率。横坐标是运行时间。

高斯核（非线性核）

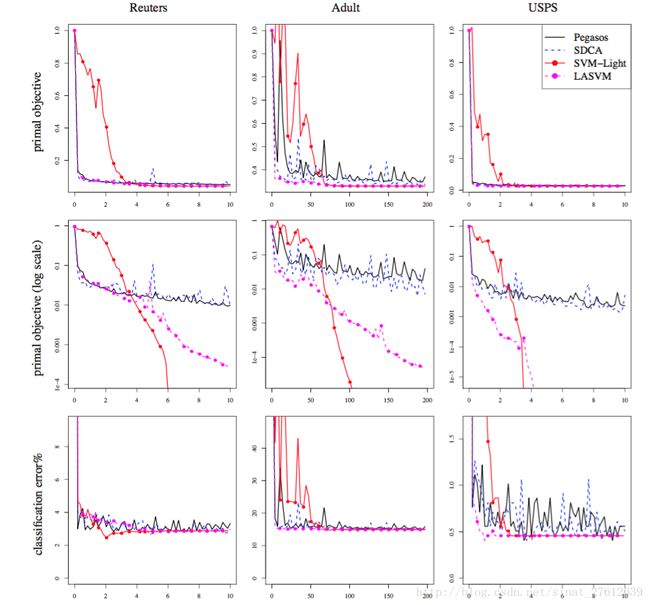
第一行是原目标函数的收敛曲线，第二行是log归约后的目标函数收敛曲线，第三行是分类误差率。横坐标是运行时间。

python实现：
https://github.com/changtingwai/pegasos