Latex-TiKZ绘制数学平面几何图教程

本文专注于Latex 文档中的 数学图形 绘制 ，更准确一点的说法是 平面几何图形 绘制。

Latex常用语法请参考我的另一篇文章《中文版Latex常用语法大全教程》

Latex上画 平面几何图形 的包是 \usepackage{tikz} ，本文所有的示例都是基于该宏包演示的，演示用的Latex 环境配置，请参考我的另一篇文章《ubuntu20.04下vim+vimtex编写latex的利器》。

要是想绘制三维图，请参考我的另外一篇文章《Latex-pgfplots绘制3维曲线图》

这里再啰嗦几句，数学上的平面几何图形主要有以下 4 大类：

• 点
• 线
• 面
• 立体

这几大类，在本文都会介绍，我会实时更新，请广大道友，持续关注……

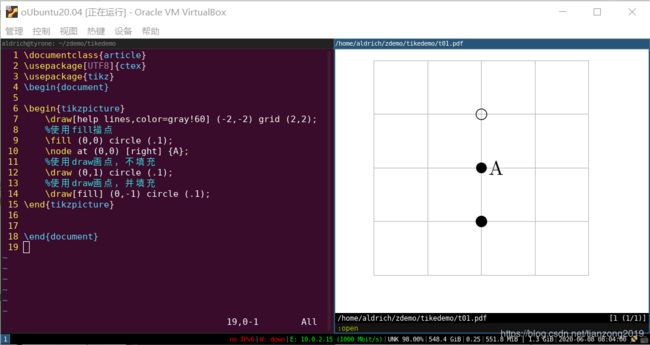
你好china

这里的“hello world”，我准备以画点并标注上标识来演示。

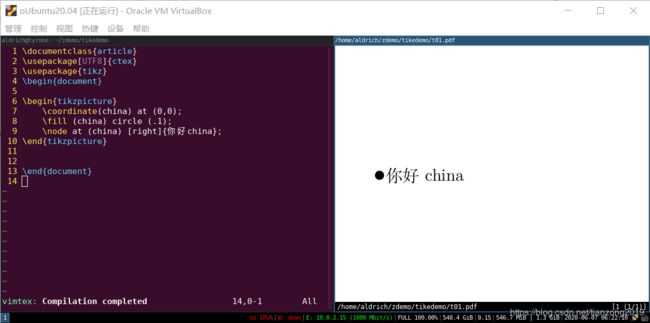
我们先来分析下这个“hello world”：

• \usepackage{tikz}
  使用tikz画图时，先来导入宏包

• \coordinate(china) at (0,0);
  有人说这是画点语法，而我却认为，这是一个标记点的语法，或者说是给“点”定义一个变量，下面根据变量名来引用点。

• \fill (china) circle (.1);
  这是一个填充的语法，语义是填充一个点，圆形，半径是0.1cm（这里有没有感觉到奇怪？）。
  我认为这才是画点的语句，在点“china”坐标处画点，画的是一个圆点。

• \node at (china) [right]{你好china};
  这个语句是在点“china”坐标的 右边 写上一个标识，来说明这个点，可以是“A”、“B”等其他的，或者是你想标注的其他一个字符。
  
  
  通过这个示例，大家是不是清晰了，更有趣的还在后面，请大家尽情期待吧……
  
  

基本图形

辅助网格

在介绍所有图形的绘制前，我认为应该先介绍下辅助网格的绘制，这个在以后的图形绘制中帮助很大，也便于各位同学在绘制时的理解。

绘制辅助网格的语法：

\draw[help lines [,color=颜色值!该色百分比[,step=网格大小]]] (左下角坐标坐标) grid (右上角坐标) ;

• 颜色值    辅助网格的颜色值
• 该色百分比     表示辅助网格颜色值的深浅明暗，如：!50 表示该色的50%
• 网格大小     表示网格以多大尺寸绘制，不写的话，会默认以1cm大小绘制，如：10pt，指的是以10像素大小绘制，也可以使用实数，如1.5cm，不过不能写成1.5pt，因为像素已经是最小单位，只能用整数。
• 左下角坐标     辅助网格是个矩形（正方形），需要先填写左下角坐标
• 右上角坐标     与“左下角坐标坐标”同理。

比如“hello world”中的语句 “ \fill (china) circle (.1);”，其中 “.1” 指的就是0.1cm，如果把 “.1” 写成 “1pt” ，表示的就是1像素，下面通过示例来演示我本机电脑上的 1cm 跟 1pt 的关系。

演示之前，再来介绍下node的语法，也就是做标记，标注：

\node at (坐标点) [方位] {标注内容}；

• 坐标点     就是准备对哪个点做标注，就填写哪个点的坐标
• 方位     标注的文字要放在标注点的哪个方向（上下左右），above、below、left、right
• 标注内容     就是要标注什么内容？可以是中文字符，也可以是西文字符

示例及效果

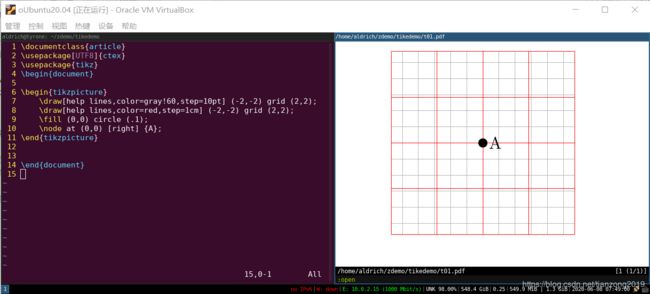
从上图可以看出，本机上的“1cm” 稍微小于 “30pt”，我当时核对过本机数据，1cm ≈ 28.5pt，机器不同，或许这个数据也不同，大家不要太纠结。

示例中使用到了 fill 语法，这个就是填充语法，不单独介绍，在后文中用到哪一点就演示哪一点。

点

画点也叫描点，其语法我认为有2种，一种是：

• \fill (0,0) circle (.1);   %在坐标（0,0）点，绘制圆点
• \draw[fill] (1,1) circle (.1);   %在坐标（1,1）点，绘制圆点

不过，这两种方式在实现上有一点区别：

• fill     在指定点，进行 点 的填充，并需指定填充的形状和范围大小
• draw     在指定点，进行 画图并填充，也需绘制的形状和范围大小，并配置是否填充，带 fill 参数，表示绘图并填充，不带时表示，绘图不填充。

示例及效果如下：

直线

绘制直线的语法：

\draw [option] (起点坐标) - - (终点坐标) ；

• option     是绘制直线的样式，比如，颜色，粗细等，多个option间用逗号 “,” 隔开
• 起点坐标     绘制一个线段就要有起点和终点，指定了2点，才能在2点间画直线
• 终点坐标     与起点坐标同理
• - -     看到公式中的2个短划线了，在实际绘制时，2个短划线之间没有空格，这个写上空格，以便于阅读。

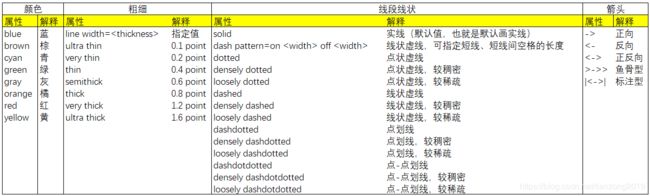
知道了直线的基础语法，我们再来说下，直线有哪些样式，或者说是属性：颜色、粗细、箭头、形状。

其中颜色、粗细、形状，这个几个属性是所有的平面几何图形所共有的属性：

• 颜色     使用 color 关键字指定
• 粗细     可使用关键字 line width 指定线宽值，也可使用粗细关键字“thin、thick”，程度关键字“ultra 、very”相互组合
• 箭头     一般使用 “-” 、 “>” 和 “<” 相互组合成不同的箭头的形状
• 形状     这里的形状指的是：实线、点状虚线、线状虚线、点画线等

下面画了一个表格，来对以上option做个介绍，以供参考。

下面的演示示例，会组合以上option做演示，但有演示不到的情况请大家自己实践。

备注：画线的演示程序都使用thick来指定线宽，太细时，不容易看清，大家可自己实现其他线宽。



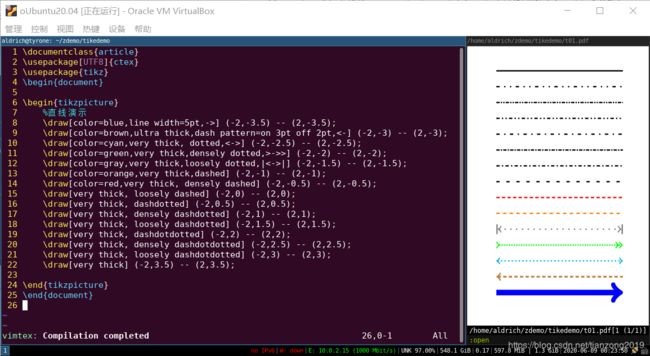
绘制多个线段，可是其闭合，其关键字就是 cycle，示例：

• \draw (1,3)–(2,2)–(4,5)–cycle;

矩形

绘制矩形的语法：

\draw [option] (起点坐标) rectangle (终点坐标) ；

• option     是绘制线段的属性，但是没有箭头
• 起点坐标     矩形左下角坐标
• 终点坐标     矩形右上角坐标

示例及效果如下



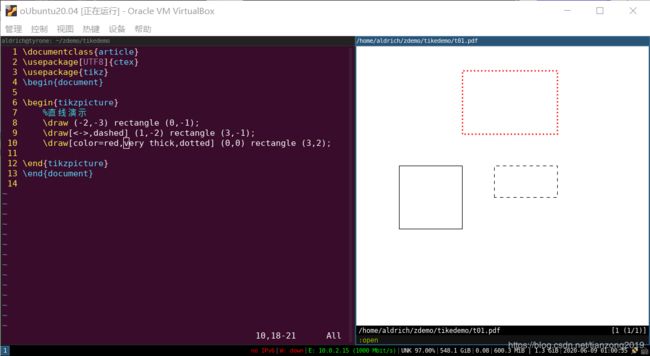
矩形还有一个 圆角 的属性，“rounded corners”，示例：

• \draw[rounded corners] (0,0) rectangle (4,2);

圆

语法：

\draw [option] (圆点坐标) circle （半径）;

• option     同矩形解释
• 圆点坐标     画圆时需要先指定圆心坐标
• 半径     再指定圆半径

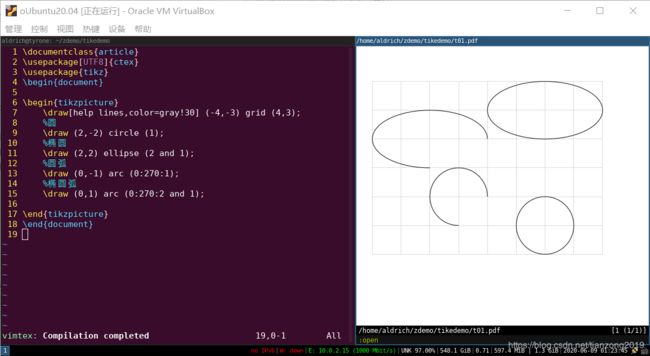
椭圆

语法：

\draw [option] (圆点坐标) ellipse （长轴 and 短轴）;

• option     同矩形解释
• 圆点坐标     画椭圆时需要先指定圆心坐标
• 长轴     画椭圆时需要指定长轴大小
• 短轴     画椭圆时需要指定短轴大小

弧

弧分为 圆弧 和 椭圆弧，语法：

圆弧

• \draw [option] (圆心坐标) arc (起始度 : 终止度 : 半径);
  1. option     同矩形解释
  2. 圆心坐标     画弧时也需要指定，该弧所在圆心坐标
  3. 起始度     弧也会分起始所在度数 和 终止所在度数
  4. 终止度     弧也会分起始所在度数 和 终止所在度数
  5. 半径     弧所在圆的半径大小

椭圆弧

• \draw [option] (圆心坐标) arc (起始度 : 终止度 : 长轴 and 短轴);
  1. option     同矩形解释
  2. 圆心坐标     画弧时也需要指定，该弧所椭圆的圆心坐标
  3. 起始度     弧也会分起始所在度数 和 终止所在度数
  4. 终止度     弧也会分起始所在度数 和 终止所在度数
  5. 长轴     弧所在椭圆的长轴和短轴大小
  6. 短轴     弧所在椭圆的长轴和短轴大小

注意：上述起始度、终止度 和半径之间是冒号 “：”分割，椭圆弧也是一样。

下面做个示例，演示圆、椭圆、弧的效果

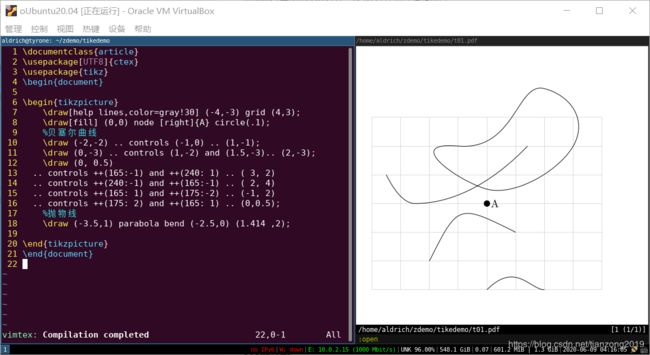
曲线

说到曲线，就不得不提 贝塞尔曲线，由起始点、终止点（也称锚点）、控制点组成。通过调整控制点，贝塞尔曲线的形状会发生变化。对贝塞尔曲线感兴趣的，可查看《贝塞尔曲线的数学原理》。

tikz绘制曲线时把直线的短线 - - 换成点 . . ，就得到贝塞尔曲线，它需要至少一个控制点，最多2个控制点，如果要画复杂的曲线时，可以使用多段曲线实现。

而抛物线用parabola 操作，bend 操作可以指明顶点。

语法如下：

贝塞尔曲线

• \draw [option] (起点坐标) . . controls (控制点1) and (控制点2)… (终点坐标) ；

1. option     同矩形解释
2. 起点坐标     既然要画曲线，就会有起点和终点坐标
3. 控制点     tikz绘制一段贝塞尔曲线，需要至少1个，最多2个控制点

抛物线

• \draw [option] (起点坐标) parabola bend (顶点) (终点坐标) ；

1. option     同矩形解释
2. 起点坐标     抛物线也需要起点和终点坐标
3. 顶点     抛物线也需要顶点坐标

示例及效果如下

示例中使用了符合“++”，这个属于图形平移，会在后面介绍。

坐标轴

其实坐标轴的绘制是直线绘制的综合，因为坐标轴是有多个直线段组成的，直接上示例：

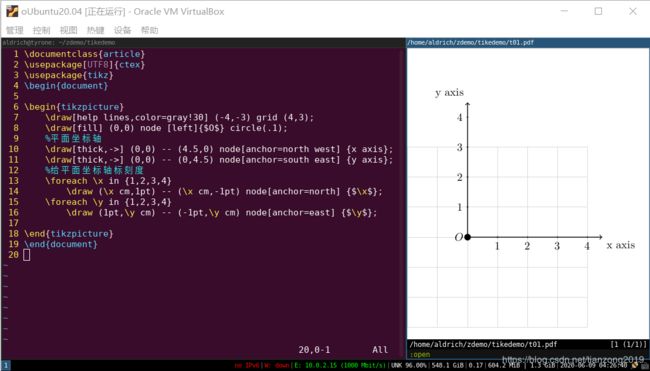
这里演示的是2维坐标轴，当然也可以绘制3维坐标轴，里面使用了一个命令 foreach，这个以前没有说过，用于引用循环变量及其文本格式。语法：

\foreach var in {list}
* 使用变量var从list中遍历

当然也可以同时遍历2个变量，格式
\foreach a/b in {list}
* 这里把a/b作为一个整体，用“/”分割，所以list的元素也必须是形为“a/b”，用“/”分割。

图形控制

这里主要说下点的偏移、缩放(scale)、平移(shift)、倾斜(slant) 、旋转(rotate)、定点旋转(rotate around) 等。

先来补充一个知识点，极坐标，在上面的图形绘制中，除了可以使用平面坐标，也可以使用极坐标。tikz中的点也支持极座标表示，(30:1cm)，第一个参数是极座标里面的角度，第二个参数是半径。

我们一般画直线时，使用的时 2维平面坐标，当然也可以填写 3维坐标。

• \draw[color=red] (0,2,0) – (0,0.5,0); %大家可以自行实现该效果
  
  

点的偏移

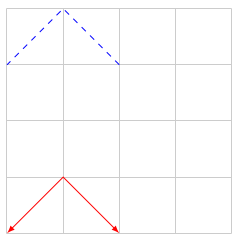
先来看下如下程序段

 7 \begin{tikzpicture}[scale=2]
 8 \draw[step=1,color=gray!40] (-2,-2) grid (2,2);
 9 \draw[latex-latex, red] (0,-2) -- ++(-1,1) -- ++(-1,-1);
10 \draw[dashed, blue] (0,1) -- +(-1,1) -- +(-2,0);
11 \end{tikzpicture}

看不懂没有关系，我们慢慢爱解说。tikz中有一个重要的概念，当前点，然后点可以通过当前点根据相对偏移来确定一个新的点。上面代码第9行的 ++ 符号和第10行的 + 符号都根据当前点然后进行了 $\Delta x$ 和 $\Delta y$ 的相对偏移从而确定了一个新的点。这两个符号的区别在于是不是更新当前点数据。++符号更新当前点，而+符号不更新。

++适合描述一连串逐渐变化的点，+适合描述多个点围绕着一个点变化的情况。

另外除了上文所示的“coordinate”是定义点的变量外，node也具有相同功能，格式：

• \node (node001) at (0,2) [fill]{};
• 1. 其中“[fill]”，是说在标记点填充，以便该点在平面图上标识出来，默认填充的是矩形
• \node (node001) at (0,2) [fill,circle]{}; %该命令，可填充为圆点

两个点定义出一个点

tikz的另外一个好玩的用法，用2个点定义出一个点，先看示例：

\begin{tikzpicture} 
\node (p1) at (30:1) {$p_1$} ; 
\node (p2) at (75:1) {$p_2$} ; 
\draw (-0.2,0) -- (1.2,0) node[right] (xline) {$q_1$}; 
\draw (2,-0.2) -- (2,1.2) node[above] (yline) {$q_2$}; 
\draw[->] (p1) -- (p1 |- xline); 
\end{tikzpicture}

这种形式 (p1 |- xline) 表示取第一个点的x和第二个点的y组成一个新的点。如果是 (p1 -| xline) 表示取第二个点的x和第一个点的y组成一个新的点。

平移

该命令为：

• shift    整体平面，需要指定平移后左下角的坐标点
• xshift     沿 $x$ 方向平移，需指定自定义平移距离
• yshift     沿 $y$ 方向平移，需指定自定义平移距离

示例如下：

\begin{tikzpicture}
\draw (0,0) rectangle (2,2);
%整体平移
\draw[shift ={(3 ,0)}] (0,0) rectangle (2,2);
\draw[shift ={(0 ,3)}] (0,0) rectangle (2,2);
%左右平移
\draw[xshift =100pt] (0,0) rectangle (2,2);
\draw[xshift =-100pt] (0,0) rectangle (2,2);
\draw[yshift =100pt] (0,0) rectangle (2,2);
\draw[yshift =-100pt] (0,0) rectangle (2,2);
\end{tikzpicture}

更换坐标后，请大家自行演示……

缩放

该命令为：

• xscale = a：指定水平方向缩放[公式]倍。若 [公式] 则代表水平方向放大（水平拉长）；若 [公式] 则代表水平方向缩小（水平缩短）；
• yscale = a：指定竖直方向缩放[公式]倍。若 [公式] 则代表竖直方向放大（竖直拉长）；若 [公式] 则代表竖直方向缩小（竖直缩短）
• scale = a：指定整体缩放 [公式] 倍。若 [公式] 则代表整体放大；若 [公式] 则代表整体缩小；

示例如下：

\begin{tikzpicture}
\draw (0,0) rectangle (2,2);
%左右缩放
\draw[xshift =70pt ,xscale =1.5] (0,0) rectangle (2,2);
\draw[yshift =70pt ,yscale =1.5] (0,0) rectangle (2,2);
\draw[xshift =-70pt ,xscale =0.5] (0,0) rectangle (2,2);
\draw[yshift =-70pt ,yscale =0.5] (0,0) rectangle (2,2);
%整体缩放
\draw[shift ={(3,0)},scale =1.5] (0,0) rectangle (2,2);
\draw[shift ={(-2 ,0)},scale =0.5] (0,0) rectangle (2,2);
\end{tikzpicture}

更换坐标后，请大家自行演示……

旋转

使用 rotate 命令实现旋转效果，示例：

\begin{tikzpicture}
\draw (0,0) rectangle (2,2);
\draw[xshift =125pt ,rotate =45] (0,0) rectangle (2,2);
\end{tikzpicture}

rotate 后面的数值写要旋转的角度，正数表示逆时针旋转相应角度，而负数表示顺时针旋转相应角度，这与数学上的正方向规定是一致的。

倾斜变换

使用 xslant 和 yslant 命令实现，示例：

\begin{tikzpicture}
\draw (0,0) rectangle (2,2);
\draw[xshift =70pt ,xslant =1] (0,0) rectangle (2,2);
\draw[yshift =70pt ,yslant =1] (0,0) rectangle (2,2);
\end{tikzpicture}

定点旋转

旋转时，可以指定一个点，围绕其进行旋转，示例：

\begin{tikzpicture}
\draw (0,0) rectangle (2,2);
\draw[xshift =125pt ,rotate =45] (0,0) rectangle (2,2);
\draw[xshift =175pt ,rotate around ={45:(2 ,2)}] (0,0) rectangle (2,2);
\end{tikzpicture}

定点旋转的只需要在rotate aroun 后面的{}中写上旋转的角度和指定点的坐标即可。旋转的方向与非定点旋转时的方向规定一致。

函数图形

tikz宏包还可以帮助绘制函数图像，比如：

\begin{tikzpicture}
\draw[->] (-0.2,0) --(6,0) node[right] {$x$};
\draw[->] (0,-0.2) --(0,6) node[above] {$f(x)$};
\draw[domain =0:4] plot (\x ,{0.1* exp(\x)}) node[right] {$f(x)=\frac{1}{10}e^x$};
\end{tikzpicture}

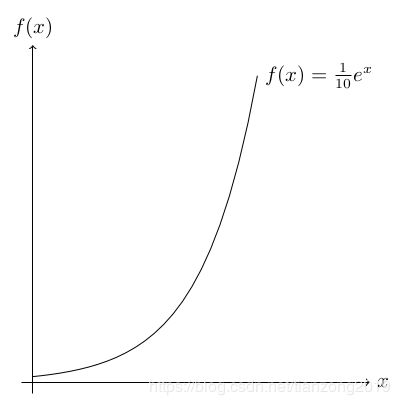
其中domain 设置了我们想要绘制的范围，起始点和终止点之间用 : 隔开。plot 是绘制操作，node后面[]中填写我们文本的位置。

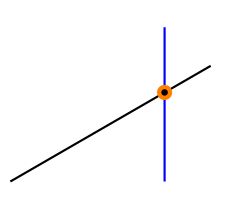
两直线或曲线的交点

再补充一个知识点，就是“两条直线或曲线的交点”，画几何图，难免的会要求标注交点。下面直接用示例解释。

注意：绘制交点时，要加上包 “\usetikzlibrary{intersections}”

  1 \documentclass{article}
  2 \usepackage[UTF8]{ctex}
  3 \usepackage{tikz}
  4 \usetikzlibrary{intersections}
  5 \begin{document}
  6 \begin{tikzpicture}
  7 \path [draw,name path=upward line][blue] (1,0) -- (1,1);
  8 \path [draw,name path=sloped line] (0,0) -- (30:1.5cm);
  9 %   
 10 \draw [name intersections={of=upward line and sloped line, by=x}]
 11 [thick,orange,fill=black]  (x) circle(1pt);
 12 
 13 \end{tikzpicture}
 14 \end{document}

第7行绘制一条从(1,0)到(1,1)的命名为“upward line”的蓝色直线
第8行同理
第10、11行在2条直线的交点处，绘制交点，需要注意的是其中的关键字:

• name intersections={of=xx1 and xx2, by=x}，这个是定义交点的语法，其他的部分都是，描述交点的属性。“xx1” 是目标线1，“xx2”是目标线2，二者的交点命名为“x”。
  
  下面多写几个示例（来自网络），以供大家对比参考。

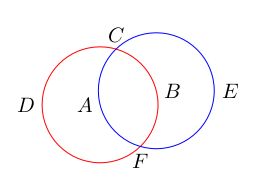
示例01，标注两个圆的交点：

  1 \documentclass{article}
  2 \usepackage[UTF8]{ctex}
  3 \usepackage{tikz}
  4 \usetikzlibrary{through}
  5 \usetikzlibrary{intersections}
  6 \begin{document}
  7 \begin{tikzpicture}
  8 \coordinate [label=left:$A$] (A) at (0,0);
  9 \coordinate [label=right:$B$] (B) at (1,0.25);
 10 \node (D) [name path=pathD,draw,red,circle through=(B),label=left:$D$    ] at (A) {};
 11 \node (E) [name path=pathE,draw,blue,circle through=(A),label=right:$    E$] at (B) {};
 12 % 命名交点坐标,但是不画出来:
 13 \path [name intersections={of=pathD and pathE}];
 14 % 标注第一个交点坐标C
 15 \coordinate [label=above:$C$] (C) at (intersection-1);
 16 % 标注第二个交点坐标F
 17 \node[below] at (intersection-2){$F$};
 18 
 19 \end{tikzpicture}
 20 \end{document}

示例02：

  1 \documentclass{article}
  2 \usepackage[UTF8]{ctex}
  3 \usepackage{tikz}
  4 \usetikzlibrary{intersections}
  5 \begin{document}
  6 \begin{tikzpicture}
  7 %定义坐标,并标注为A B C D
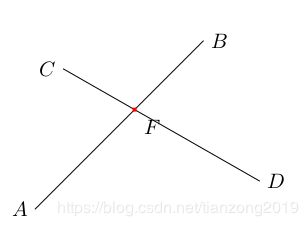
  8 \coordinate [label=left:$A$] (A) at (0,0);
  9 \coordinate [label=right:$B$] (B) at (3,3);
 10 \coordinate [label=left:$C$] (C) at (0.5,2.5);
 11 \coordinate [label=right:$D$] (D) at (4,0.5);
 12 %画直线
 13 \draw [name path=A--B] (A) -- (B);
 14 \draw [name path=C--D] (C) -- (D);
 15 % 使用by=可以命名交点坐标为F,但是不画出来:
 16 \path [name intersections={of = A--B and C--D,by=F}];
 17 %标注交点坐标F
 18 \node [fill=red,inner sep=1pt,label=-45:$F$] at (F) {};
 19 
 20 \end{tikzpicture}
 21 \end{document}

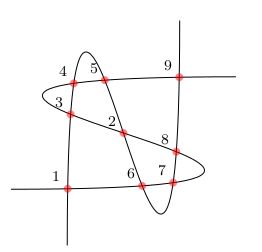
示例03，更复杂的交点标注：

  1 \documentclass{article}
  2 \usepackage[UTF8]{ctex}
  3 \usepackage{tikz}
  4 \usetikzlibrary{intersections}
  5 \begin{document}
  6 \begin{tikzpicture}
  7 %定义一个矩形,所有的绘图命令只在矩形内有效
  8 \clip (-2,-2) rectangle (2,2);
  9 %画任意的两条贝赛尔曲线
 10 \draw [name path=curve 1] (-2,-1) .. controls (8,-1) and (-8,1) .. (2    ,1);
 11 \draw [name path=curve 2] (-1,-2) .. controls (-1,8) and (1,-8) .. (1    ,2);
 12 %标注每个交点坐标
 13 \fill [name intersections={of=curve 1 and curve 2, name=i, total=\t}]
 14 [red, opacity=0.5, every node/.style={above left, black, opacity=1}]
 15 \foreach \s in {1,...,\t}{(i-\s) circle (2pt) node {\footnotesize\s}}    ;
 16 %name=i设置交点前缀,i-\s为每个交点的名称
 17 %total=\t表示交点总数目
 18 
 19 \end{tikzpicture}
 20 \end{document}

示意图

tikz也支持绘制 流程图 和 树形图，直接上示例（来自网络）：
先定义一个属性变量：

\tikzset{
box/.style ={
rectangle, %矩形节点
rounded corners =5pt, %圆角
minimum width =50pt, %最小宽度
minimum height =20pt, %最小高度
inner sep=5pt, %文字和边框的距离
draw=blue %边框颜色}
}

绘制流程图

\begin{tikzpicture}
\node[box] (1) at(0,0) {1};
\node[box] (2) at(4,0) {2};
\node[box] (3) at(8,0) {3};
\draw[->] (1)--(2);
\draw[->] (2)--(3);
\node at(2,1) {a};
\node at(6,1) {b};
\end{tikzpicture}

绘制树形图

\begin{tikzpicture}[sibling distance =80pt]
\node[box] {1}
    child {node[box] {2}}
    child {node[box] {3}
        child {node[box] {4}}
        child {node[box] {5}}
        child {node[box] {6}}
    };
\end{tikzpicture}

要记得定义 sibling distance 属性，要不然，节点会堆在一起。child 关键字用来声明子节点；sibling distance 选项可以控制相邻节点之间的距离，单位为pt。

另外tikz主要用在绘制平面几何图形，我之后会再整理一篇可绘制 3维曲线图的文档，请感兴趣的同学，持续关注啊……

立体

直接上示例，有不熟悉的，请留言讨论 ^ _ ^

参考资料

1. https://zhuanlan.zhihu.com/p/127155579