KMP算法的实现(Java)
KMP算法的实现(Java)
KMP算法
- KMP算法的实现(Java)
- 简介
- 问题
- 暴力算法(Brute Force)
- KMP算法
- next数组的计算
- 1. 找出最长的相同的前缀和后缀
- 2. next数组
- 3. 代码实现
- 4. next数组优化
- 参考
简介
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现,函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)。
问题
有一个目标串S,和一个模式串P,现在要寻找模式串P是否在目标串S 中,及其出现的位置,怎么查找呢?
暴力算法(Brute Force)
用暴力算法匹配字符串过程中,我们会把S[0] 跟 P[0] 匹配,如果相同则匹配下一个字符,直到出现不相同的情况,此时我们会丢弃前面的匹配信息,然后把S[1] 跟 P[0]匹配,循环进行,直到主串结束,或者出现匹配成功的情况。这种丢弃前面的匹配信息的方法,极大地降低了匹配效率。
假设现在目标串S匹配到 i 位置,模式串P匹配到 j 位置,则有:
- 如果当前字符匹配成功(即S[i] == P[j]),则i++,j++,继续匹配下一个字符;
- 如果失配(即S[i]! = P[j]),令i = i - (j - 1),j = 0。相当于每次匹配失败时,i 回溯,j 被置为0。
/**
* Brute Force: O(mn)
* @param s 目标串
* @param p 模式串
* @return 如果匹配成功,返回下标,否则返回-1
*/
public static int stringMatch(String s, String p) {
if (s.equals(p)) {
return 0;
}
if (s.length() < p.length()) {
return -1;
}
int i = 0, j = 0;
while (i < s.length() && j < p.length()) {
// 如果当前字符匹配成功(即S[i] == P[j]),则i++,j++,继续匹配下一个字符
if (s.charAt(i) == p.charAt(j)) {
i++;
j++;
} else {
// 如果失配(即S[i]! = P[j]),令i = i - (j - 1),j = 0。相当于每次匹配失败时,i 回溯,j 被置为0
i = i - j + 1;
j = 0;
}
}
if (j == p.length()) {
return i - j;
} else {
return -1;
}
}
KMP算法
在KMP算法中,对于每一个模式串我们会事先计算出模式串的内部匹配信息,在匹配失败时最大的移动模式串,以减少匹配次数。
在简单的一次匹配失败后,我们会想将模式串尽量的右移和主串进行匹配。右移的距离在KMP算法中是如此计算的:在已经匹配的模式串子串中,找出最长的相同的前缀和后缀,然后移动使它们重叠。
假设现在文本串S匹配到 i 位置,模式串P匹配到 j 位置:
- 如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++,继续匹配下一个字符;
- 如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]。此举意味着失配时,模式串P相对于文本串S向右移动了j - next [j] 位。
- 换言之,当匹配失败时,模式串向右移动的位数为:失配字符所在位置j - 失配字符对应的next 值,即移动的实际位数为:j - next[j],且此值大于等于1。
next 数组各值的含义:代表当前字符之前的字符串中,有多大长度的相同前缀后缀。例如如果next [j] = k,代表j 之前的字符串中有最大长度为k 的相同前缀后缀。
在某个字符失配时,该字符对应的next 值会告诉你下一步匹配中,模式串应该跳到哪个位置(跳到next [j] 的位置)。如果next [j] 等于0或-1,则跳到模式串的开头字符,若next [j] = k 且 k > 0,代表下次匹配跳到j 之前的某个字符,而不是跳到开头,且具体跳过了k 个字符。
在第一次匹配过程中:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| s | a | b | a | c | a | b | a | b | c |
| p | a | b | a | b | |||||
| j | 0 | 1 | 2 | 3 |
s[3] 与 p[3]出现不匹配,而s[0]~s[2]是匹配的,其中s[0] ~ s[2] 就是上文中说的已经匹配的模式串子串,移动找出最长的相同的前缀和后缀并使他们重叠:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| s | a | b | a | c | a | b | a | b | c |
| p | a | b | a | b | |||||
| j | 0 | 1 | 2 | 3 |
然后在从上次匹配失败(i = 3)的地方进行匹配,这样就减少了匹配次数,增加了效率。
next数组的计算
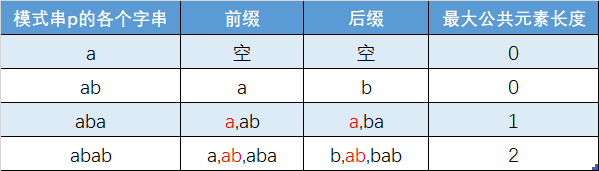
1. 找出最长的相同的前缀和后缀
2. next数组
next 数组相当于“最大长度值” 整体向右移动一位,然后初始值赋为-1,即

/**
* Table building: O(m)
*
* @param p 匹配串
* @return
*/
private static int[] getNext(String p) {
int len = p.length();
int[] next = new int[len];
next[0] = -1;
int i = 0, k = -1;
while (i < len - 1) {
// p[k]表示前缀,p[i]表示后缀
if (k == -1 || p.charAt(i) == p.charAt(k)) {
++k;
++i;
next[i] = k;
} else {
k = next[k];
}
}
return next;
}
3. 代码实现
/**
* O(m+n)
*
* @param s 目标串
* @param p 模式串
* @return 如果匹配成功,返回下标,否则返回-1
*/
private static int kmpSearch(String s, String p) {
int sLen = s.length();
int pLen = p.length();
if (sLen < pLen) {
return -1;
}
int[] next = getNext(p);
// matching: O(n)
int i = 0, j = 0;
while (i < sLen && j < pLen) {
//①如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++
if (j == -1 || s.charAt(i) == p.charAt(j)) {
i++;
j++;
} else {
//②如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]
//next[j]即为j所对应的next值
j = next[j];
}
}
if (j == pLen) {
return i - j;
} else {
return -1;
}
}
4. next数组优化
/**
* Table building: O(m)
* 优化的next数组
* @param p 匹配串
* @return
*/
private static int[] getNext2(String p) {
int len = p.length();
int[] next = new int[len];
next[0] = -1;
int i = 0, k = -1;
while (i < len - 1) {
// p[k]表示前缀,p[i]表示后缀
if (k == -1 || p.charAt(i) == p.charAt(k)) {
++k;
++i;
if (p.charAt(i) != p.charAt(k)) {
next[i] = k;
} else {
// 因为不能出现p[i] = p[next[i]],所以当出现时需要继续递归,k = next[k] = next[next[k]]
next[i] = next[k];
}
} else {
k = next[k];
}
}
return next;
}
参考
- 从头到尾彻底理解KMP
- KMP算法
- KMP Algorithm for Pattern Searching
- Knuth–Morris–Pratt algorithm