60. 第k个排列(python)

题目描述

给出集合 [1,2,3,…,n]，其所有元素共有 n! 种排列。

按大小顺序列出所有排列情况，并一一标记，当 n = 3 时, 所有排列如下：

1. "123"
2. "132"
3. "213"
4. "231"
5. "312"
6. "321"

给定 n 和 k，返回第 k 个排列。

说明：

• 给定 n 的范围是 [1, 9]。
• 给定 k 的范围是[1,  n!]。

示例 1:

输入: n = 3, k = 3
输出: "213"

示例 2:

输入: n = 4, k = 9
输出: "2314"

思路分析

通过观察，我们可以看到 n 个数字共有 n ! 个排练组合：排列的第一个字符从 n 个中选择1个，第二个字符从剩下的n-1个里面选择1个……所以，当所有组合字符串按顺序排列后，以“ 1 ”开头的有（n-1）！个组合，以" 1 “或者 2 ”开头的有 （n-1）!+(n-1)! = 2*(n-1) ! 个组合，……

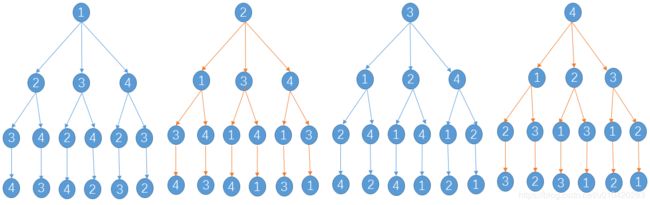
以 n=4 为例，将所有的排列组合画出我们更容易看出规律。

找到规律后，我们可以这样来解题：记num ="123...n"，确定所有排列组合中第 k 个字符串从左到右（用 j 表示，j 从1：n）每个位置是什么，算法流程如下：

令 i = n : 1

m=k/(i-1)

现在分两种情况：

1. 刚好整除：表示在排列组合树的前一个分支中刚好结束，输出字符串是上一个分支中的最后一个字符串组合：得到分支根部字符，即：num[m-1]；然后从num中去除此字符，将剩下字符从大到小即为 k 剩余位置字符的排列。

2. 不能整除，有余数：获取当前分支的根部，即是本轮确定的输出字符串第 j 个字符为num[m]。更新k的值： k=k%(n-1)。

整个过程一旦达到第1种情况，就返回所求第 k 个字符串的值，提前退出循环；否则即使从n到1最终也肯定会达到整除的那一步。

代码实现

def getPermutation(self, n, k):
        """
        :type n: int
        :type k: int
        :rtype: str
        """
        num='123456789'
        num=num[:n]
        res=''
        for i in range(n,0,-1):
            m = k // math.factorial(i-1)
            k = k % math.factorial(i-1)
            if k==0:
                res = res + num[m-1]
                num = num.replace(str(num[m-1]), '')
                return res+num[::-1]
            res = res + num[m]
            num = num.replace(str(num[m]), '')