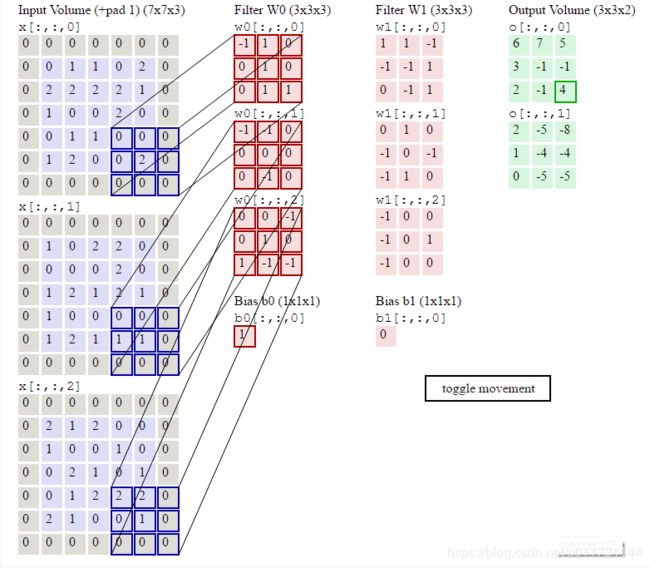
二维卷积神经网络的结构理解
针对这个图,我们对应着卷积的api函数来说:
tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, name=None)
如上图:
第一列为一张输入图像, 大小为7*7*3, 即宽高为7*7, 通道数为3
所以inputs的维度就是: [-1, 7, 7, 3] , -1是表示batch的大小可以随意,基于输入决定
第二列和第三列为一个卷积层, 对应着参数filter, 它是一个4d的参数, 分别为卷积层的高,宽,图像通道数,卷积核数
宽高很显然是3*3, 就是第二列或者第三列里面的一个红色的矩形的宽高
图像通道数,对应着输入图像的通道数,也就是3,也就是第二列Filter W0或W1中的3*3矩形的个数, 可以看到上面第一列和第二列之间的连线,说明第一列的7*7的矩形个数和第二列的3*3的矩形个数要一致,都是图像的通道数
卷积核数,就是第二列到第三列的列数,只有两列,所以卷积核数是2, 一个卷积核是指整个第二列或第三列, 卷积核不是那个3*3的矩形,是整个第二列的3个3*3的矩形的组合, 所以整个第二列是一个卷积核,第三列也是一个卷积核
第四列是卷积后的值
输入层和第二列的卷积核计算得到的结果为Output Volume的第一个3*3的矩阵, 这个3*3矩阵的每个元素都会加上b[0],上图是已经加后的结果
输入层和第三列的卷积核计算得到的结果为Output Volume的第二个3*3的矩阵, 这个3*3矩阵的每个元素都会加上b[1],上图是已经加后的结果
偏执b的维度及其加法规则:
偏执b是一个一维的向量,维度与卷积核数一致,也就是2, 所以b的维度是2*1
加法规则上面已经解释了, 因为b的维度与卷积核的维度一致,所以是输入层和第一个卷积核每步计算的结果要加上b[0], 输入层和第二个卷积核每步计算的结果要加上b[1]