哈夫曼树的实现、应用和证明

这里是我的个人网站：
https://endlesslethe.com/huffman-tree-tutorial.html
有更多总结分享，最新更新也只会发布在我的个人网站上。
排版也可能会更好看一点=v=

什么是哈夫曼树

给定n个权值，作为n个叶结点，构造一棵二叉树，而这棵树的特点是，有n个叶节点，叶节点的值为给定的权值。而内部节点的值为子树的权值和。
这样的二叉树有很多，但树的带权路径和达到最小，则这棵树被称为哈夫曼树。

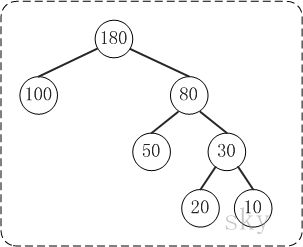
Note：带权路径和指的是所有叶节点的权值*深度和，即\(\Sigma value∗deep=100+2∗50+3∗20+3∗10\)
而我们不妨让内部节点的值为子树的权值和，我们可以发现，实际上一棵树的带权路径和=这棵树的所有节点值之和-根节点的值。（显然）

哈夫曼树有什么用

哈夫曼树主要应用在文本编码上。我们考虑如何将文本中出现的单词编码为二进制数（01串），让文本的总长度最小。
对于文本{1, 1, 2, 2, 3, 3, 3, 5}，我们可以将单词1、2、3、5出现的频率作为叶节点的权值，为{2, 2, 3, 1}。那么上述最短编码问题等价于寻找一棵树，其带权路径和最小，也就是找对应的哈夫曼树。

唯一可译码

如果我们直接将单词按照频率的从高到低排序，不就得到了一个编码了吗？
但这样的编码不是一个“唯一可译码”，即对于10001010100101，我们不能正确地分割。“唯一可译码”是通信上的概念，指的是接收到的01串可以被无二义地分割，得到唯一的表示。
而哈夫曼编码是“唯一可译码”，甚至还是“即时码”，因为后面根据编码规则，我们会看到，哈夫曼树得到的编码满足即时码的条件“任何码都不是其他码的前缀”。

最短编码问题

这里为什么说最短编码问题等价于寻找一棵带权路径长度最小的树呢？

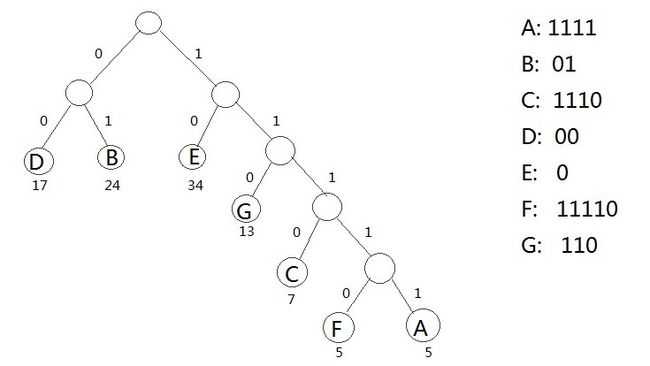
下面是对于给定一棵树的编码规则：
1. 将单词的出现次数作为叶子结点，每个字符出现次数作为该叶子结点的权值
2. 规定树中所有左分支表示字符0，所有右分支表示字符1,将依次从根结点到每个叶子结点所经过的分支的二进制位的序列作为该结点对应的字符编码
3. 由于从根结点到任何一个叶子结点都不可能经过其他叶子，这种编码一定是前缀编码，树的带权路径长度正好是文件编码的总长度

我们故如下图所示的哈夫曼树，我们不妨编码为：

Note：图中编码是因为根节点左子树的一定会有前缀0，故在对根节点右子树进行编码时省略了1。实际上是不正确的！

因为树的带权路径和正好是文件编码的总长度，而哈夫曼树的带权路径和是最小的，故对应的编码也是最优的。

构造哈夫曼树

我们已经弄清楚了哈夫曼树的应用，那么下面就讲一下怎么构造哈夫曼树。

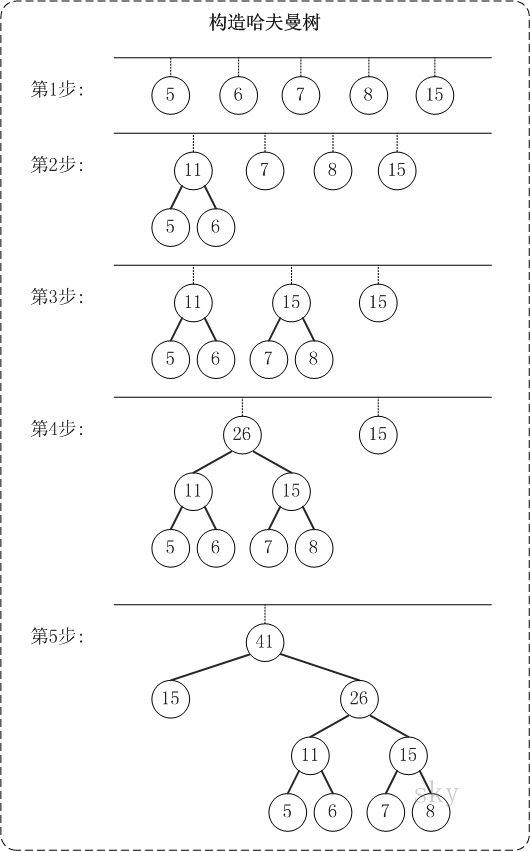
假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，哈夫曼树的构造规则为：
1. 将w1、w2、…，wn看成是有n 棵树的集合(每棵树仅有一个结点)；
2. 在森林中选出根结点的权值最小的两棵树进行合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；
3. 从集合中删除选取的两棵树，并将新树加入集合；
4. 重复(02)、(03)步，直到集合中只剩一棵树为止，该树即为所求得的哈夫曼树。

以权值{5,6,7,8,15}为例，来构造一棵哈夫曼树:

最小路径和证明

对于最小权值路径和的二叉树，有两个事实：
1. 令wi, wj 是W中权重最小的两个元素，则这两个数对应的结点是兄弟结点，且这两结点在二叉树中的深度大于其它任何一个叶结点的深度。
2. 一棵树最优树，最小的两个缩成一个，同时删除最小的两个，得到的新树还是最优树

第一个结论是显然的，因为根据反证法，如果这两个节点不是最深的，那么与最深的节点交换，树权值路径和就会减小，与假设矛盾。

第二个结论也是根据反证法：
假定T是一颗最优树，T这棵树的权值记为W（T）。最小权值的两个A，B一定在最下层，对应的路径权值分别是 Wa, Wb。
倘若删除A和B，A和B的父节C成为一个叶子节点。此时新树为T’，W(T) = W(T’)+Wa + Wb。
倘若T’不是最优树，则必定有最优树T1，满足W(T1)< W(T’)
此时若把T1中的C展开成A和B,形成新树T2 ，W(T2)=W(T1)+Wa+Wb
这样W(T2)

具体实现

因为建树的过程涉及取最小值和添加操作，所以选择使用优先队列来优化。毕竟优先队列是基于堆实现的，添加是O（logn），取最小值是O（1）。如果使用数组和链表的话，取最小值是O（1），添加是O（n）。

1. 建立优先队列
2. 建树
3. 遍历得到叶节点的编码和总权值

树的结构

struct Node {
    int v;
    Node* lson;
    Node* rson;
}

优先队列每个单元需要用Node*，只需要写一个结构体cmp重载运算符()

实现代码

/**
 * @Date:   18-Mar-2017
 * @Email:  [email protected]
 * @Filename: POJ 3253【哈夫曼树】.cpp
 * @Last modified time: 13-Aug-2018
 * @Copyright: ©2018 EndlessLethe. All rights reserved.
 */


#pragma comment(linker, "/STACK:102400000,102400000")

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;

struct Node {
    ll x;
    Node* lson, * rson;
    Node(int x, Node* lson, Node* rson):x(x),lson(lson),rson(rson){;}
    Node(int x):x(x), lson(NULL), rson(NULL){;}
//    bool operator < (const Node a, const Node b) const {
//        return a.x > b.x;
//    }
};

struct cmp {
    bool operator () (const Node* a, const Node* b) {
        return a->x > b->x;
    }
};

priority_queue vector, cmp> pq;
//priority_queue  pq;

void printNode(Node* tmp) {
    cout << tmp->x << " " << tmp->lson << " " << tmp->rson << endl;
    if (tmp->lson != NULL) {
        cout << tmp->lson->x << endl;
    }
    if (tmp->rson != NULL) {
        cout << tmp->rson->x << endl;
    }
    return;
}

ll dfs(Node* root) {
    if (root == root->lson || root == root->rson) cout << "error" << endl;
    ll res = 0;
    if (root->lson != NULL) {
        res += dfs(root->lson);
    }
    if (root->rson != NULL) {
        res += dfs(root->rson);
    }
    return res + root->x;
}

int main() {
    #ifdef LOCAL
        freopen("in.txt","r",stdin);
        freopen("test.txt","w",stdout);
    #endif
    ll N, M;
    cin >> N;
    while (N--) {
        cin >> M;
        Node *pTmp = new Node(M);
        pq.push(pTmp);//pq.push((Node){M});
    }
    while (pq.size() > 1) {
         Node* pfir = pq.top(); pq.pop();
         Node* psec = pq.top(); pq.pop();
         Node* pparent = new Node(pfir->x + psec->x, pfir, psec);
          pq.push(pparen t);
    }
    Node* root = pq.top(); pq.pop();
//    cout << "Build Completed" << endl;
    cout << dfs(root)-root->x << endl;
    return 0;
}

题目总结

• POJ 3253
• POJ 1339
• POJ 1862

参考文献

I. 哈夫曼树(三)之 Java详解
II. 哈夫曼编码问题再续（下篇）——优先队列求解
III. 字符集编码 定长与变长
IV. 信息论 惟一可译码判别方法