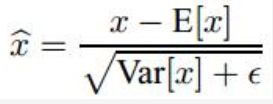深度学习中，偏置（bias）在什么情况下可以要，可以不要？

1.深度学习偏置的作用？

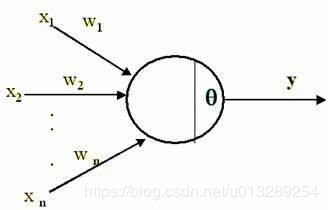
   我们在学深度学习的时候，最早接触到的神经网络应该属于感知器（感知器本身就是一个很简单的神经网络，也许有人认为它不属于神经网络，当然认为它和神经网络长得像也行）

   要想激活这个感知器，使得y=1，就必须使x1*w1 + x2*w2 +....+xn*wn > T（T为一个阈值），而T越大，想激活这个感知器的难度越大，人工选择一个阈值并不是一个好的方法，因为样本那么多，我不可能手动选择一个阈值，使得模型整体表现最佳，那么我们可以使得T变成可学习的，这样一来，T会自动学习到一个数，使得模型的整体表现最佳。当把T移动到左边，它就成了偏置，x1*w1 + x2*w2 +....+xn*wn  - T> 0   ----->x*w +b > 0，总之，偏置的大小控制着激活这个感知器的难易程度。

 

2.在某些情况下，我们是否可以不要偏置呢？

  如果大家看过我的博客：ShuffleNet V2 神经网络简介与代码实战，是否会注意到代码中的一个细节，这个代码中，bias被设置False，也就是没有用到偏置。

def conv_bn(inp, oup, stride):
    return nn.Sequential(
        nn.Conv2d(inp, oup, 3, stride, 1, bias=False),
        nn.BatchNorm2d(oup),
        nn.ReLU(inplace=True)
    )

     而在我的博客： ShuffleNet V1 神经网络简介与代码实战，这个代码中，bias被设置为True，用到了偏置

def conv3x3(in_channels, out_channels, stride=1, 
            padding=1, bias=True, groups=1):    
    """3x3 convolution with padding
    """
    return nn.Conv2d(
        in_channels, 
        out_channels, 
        kernel_size=3, 
        stride=stride,
        padding=padding,
        bias=bias,
        groups=groups)

     我这样做是不小心，还是故意而为之，大家可以猜一猜，这两份的代码区别在于卷积后面有没有接BN操作（后面我会有博客讲归一化操作，这里就不展开了）

     BN操作，里面有一个关键操作

     其中x1 = x0 * w0 + b0，而E[x1] = E[x0*w0] + b0， 所以对于分子而言，加没加偏置，没有影响；而对于下面分母而言，因为Var是方差操作，所以也没有影响（为什么没影响，回头问问你的数学老师就知道了）。所以，卷积之后，如果要接BN操作，最好是不设置偏置，因为不起作用，而且占显卡内存。