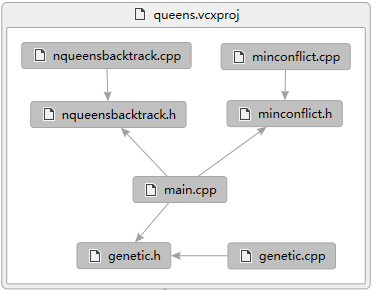
N皇后——回溯法、遗传算法、CSP最小冲突法(提供伪代码和C++源代码)
前言:8皇后耳熟能详,参考链接百度百科——八皇后。把8扩展成N,就是N皇后问题。我以下给出了解决N皇后的3个经典算法的思想和源代码(业界良心)!
1 数据结构
一个二维的棋盘,可以用一维的向量存储,我使用C++ STL中的std::vector。假设是8皇后,那么vector的大小是8,代表棋盘中的8行。vector[i] = j (0~7),代表第 i 行的皇后在第 j 列,一个vector就是一个棋盘,统称为“状态”。这样子做很巧妙地成功把二维棋盘当作一维向量保存,降低了维数。
在遗传算法中,为了保存一个种群(很多个棋盘),使用std::vector< vector< int>>,相当于二维的向量,即“向量里面的元素是一个向量”。使用STL中的vector,可以全方位提升程序的质量,比如安全性,鲁棒性等。
2 回溯法
//检测把皇后放置在棋盘位置 ( row, column ) 是否和前 row-1 行放置的皇后存在互相攻击的情况
//@param: row 是行数,column是列数
bool NQueensBacktrack::Check(int row, int column)
For i: 0 to row-1 do
If 对角线方向互相攻击,或者垂直方向互相攻击
返回 false
End if
End for
返回 true
End
回溯法(递归)有两种方法:第一种是求出所有解,第二种是求出第一个解就退出。两者之间只有两三行代码的区别。
第一种方法
//@param: row 是行数
void NQueensBacktrack::Backtrack(int row)
For column: 0 to QueenNumber-1 do
If 检测到位置(row, column)没有和皇后们互相攻击
把一个皇后放到(row, column)
If 这个皇后是在最后一行
打印此时的棋盘
End if
Backtrack(row +1),从下一行开始继续递归
End if
End for
End
第二种方法
//@param: row 是行数
//Flag 初始化为 flase
void NQueensBacktrack::Backtrack(int row)
If Flag 等于 ture
return void 递归终结
End if
For column: 0 to QueenNumber-1 do
If 检测到位置(row, column)没有和皇后们互相攻击
把一个皇后放到(row, column)
If 这个皇后是在最后一行
Flag←ture
打印此时的棋盘
End if
Backtrack(row +1),从下一行开始继续递归
End if
End for
End

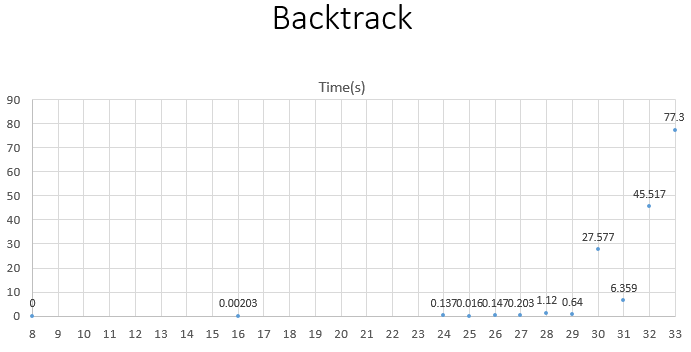
图:回溯法求解
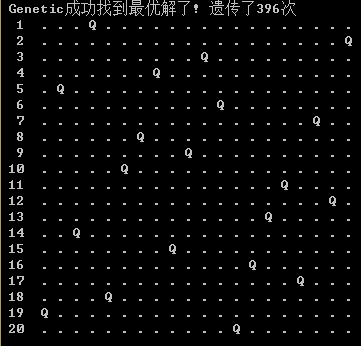
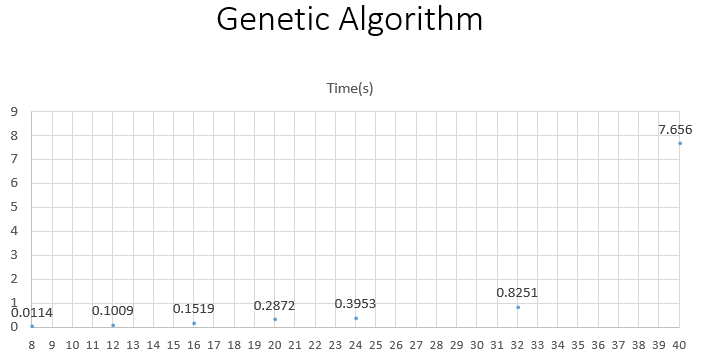
3 遗传算法
是随机剪枝搜索的一个变化形式。它通过把两个父状态结合来生成后继。算法模拟大自然的自然选择、基因杂交和变异。其中自然选择依据适应值的大小来评估被选中的概率,让更加优质的父状态更有可能传给下一代。生成种群、杂交、和变异都是依赖随机数和概率来模拟“物竞天择,适者生存”的自然法则。算法不断Select, Crossover, Mutate直到产生了一个最优解。
一个棋盘可以看成是一条染色体,统称为“状态”,一个棋盘中的皇后可以看成一个基因。我不断调整种群数量的大小、适应值函数、杂交的策略、还有变异的概率,逐渐发现了更加优秀的参数。以下是我的实验结论:
- 假设是N皇后,那么种群的数量最优是4N
- 课本《人工智能:一种现代的方法》上的适应值函数不好,稍微改进一点的适应值函数 f = 冲突皇后对的个数的倒数,这样能够拉开优质和劣质个体被选的概率。
- 课本上面的“单点+双侧”杂交(随机选择单个杂交点,这个杂交点的两侧都交换)的效果不佳,不如“单点+单侧”杂交,也不如“双点+双点之间”杂交。
- 单个基因(一个皇后)变异的概率小于0.05,比如0.04的时候,效果较好。
//主循环
void Genetic::GeneticAlgorithm()
while m_NotSuccess为真
Select
Crossover
Mutate
End while
打印最优解
End
//计算一个state(棋盘)的适应值
//适应值采用“互相攻击皇后对的个数的倒数”,这比书上直接计算不互相攻击的皇后对数作为适应值的方法相比,更能拉开不同状态之间的差距。
//@para state:一个状态的引用
double Genetic::CalcuAdaptive(vector &state)
counter←0
For i: 0 to QueenNum-1 do
For i: 0 to QueenNum-1 do
If 对角线方向互相攻击,或者垂直方向互相攻击
counter++
End if
End for
End for
If counter等于0
m_NotSucess←false,程序的循环终止条件
m_BestOne←state,保存当前的状态
End if
Return 1.0/counter
End
//自然选择,大体思路是轮盘赌选择
void Genetic::Select()
创建一个新的空种群newPopulation
For i: 1 to populationSize-1 do
m_accumuAdaptive[i]←m_accumuAdaptive[i - 1] + m_adaptive[i]
End for
totalAdaptive←m_accumuAdaptive的最后一个元素
For i: 0 to populationSize-1 do
先把totalAdaptive(这是一个实数)放大成一个整数
产生一个随机数 ,对totalAdaptive求模,得到 ran
按相同比例缩小成一个实数
用二分查找的方法,在m_ accumuAdaptive内进行查找 ran,找出位置 j
把m_population的第 j 个状态push_back到newPopulation中
End for
m_population←newPopulation
End
杂交有多种思路:
- 选择两个state状态,随机产生一个杂交点,然后对这个杂交点的右(左)边的“基因”进行交换
- 选择两个state状态,随机产生一个杂交点,然后再对这个杂交点两边的“基因”都进行交换。
- 选择两个state状态,随机产生两个杂交点,然后再对这两个杂交点之间的“基因”进行交换。
变异:
通过伪随机数,使每一个基因有0.0几的概率进行突变。突变就是用伪随机数赋值。
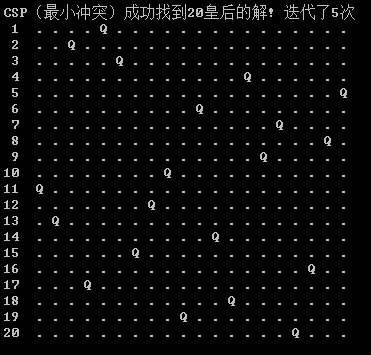
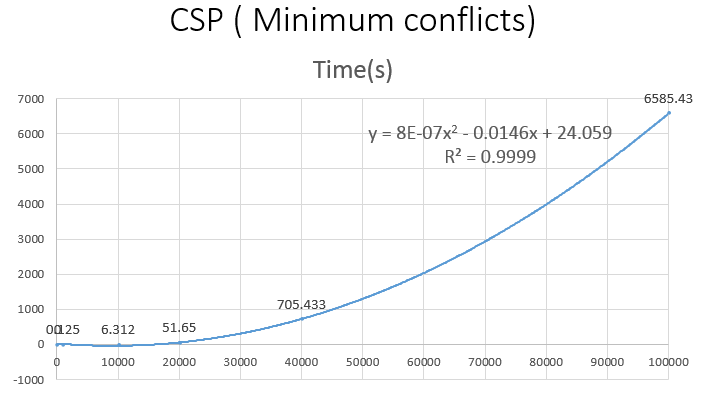
4 CSP最小冲突法
局部搜索对求解不少constraint satisfy problem有着很棒的效果。N皇后问题就是一个约束满足问题,这里的约束,就是指“皇后之间不能冲突”。该算法使用完全状态的形式化:初始状态每个变量都赋一个值,后继函数每一次改变一个变量的取值,改变取值的依据是使冲突最小化——最小冲突启发式。如果最小冲突值有多个,那么按照一定的概率选择。(经过大量反复实验发现,CSP最小冲突法存在极小概率的不完备性,即永远也找不到满足约束条件的最优解,当遇到此情况的时候,可以选择退出当前的求解,重新生成一个新的初始状态再来一次)
该算法最精彩的地方,是时间复杂度可以优化到O(n^2),于是可以在几秒内解决1万皇后的问题,在几十分钟内解决几万甚至10万皇后的问题!这是前两种算法完全无法比拟的。时间复杂度优化到O(n^2)有一点代价,那就是多付出一些空间复杂度。多出来的空间复杂度是O(n),这个和优化的时间复杂度(从O(n^4 ) 到O(n^2))相比,可以说是微不足道的,完全值得的。多出来三个vector,分别用来存储一个棋盘上的(以 8 皇后为例):
- 8个垂直方向的皇后数量
- 15个主对角线方向的皇后数量
- 15个反对角线方向的皇后数量
那么,一个皇后的冲突数量,就是这三个vector中的相应的值相加,利用下标转换关系可以做到。这样计算一个皇后的冲突数量,就可以在常数时间内完成。这是十分吸引人的!当然,每一次放置皇后和移开皇后的时候,需要更新上述三个vector的相应值,维护这三个vector也需要时间开销,不过这也是常数。
检测一个状态是否达到最优状态的时候,只需要判断每一个垂直方向(列)上面的皇后数量是否为1,主对角线和反对角线方向上的皇后数量是否是0或者1即可,这个时间复杂度是O(n)
以下是主循环的伪代码
void MinConflict::MinConflictAlgorithm()
While 没有找到最优解
For row: 0 to QueenNum-1 do
移开棋盘row这一行的皇后
更新相应的三个保存皇后数量的vector
For column: 0 to QueenNum do
计算(row, column)位置的冲突值,常数时间
If 比之前的 min 更小
更新最小值 min, 更新此时的 columnMin
Else if 和之前的最小值相等
50%概率更新最小值min,更新此时的 columnMin
End if
End for
放置皇后到冲突最小的地方(row, columnMin)
更新相应的三个保存皇后数量的vector
如果检测达到了最优状态,即找到了最优解,break For
End for
End while
打印最优解
End

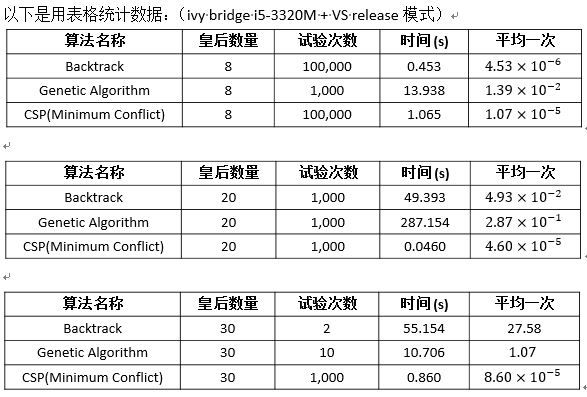
5 三种算法的比较
6 总结
求解N皇后问题。首先,是回溯法,这个不难,我的把回溯法封装到了一个类中。实际上,面向对象的思想已经深入我心,我写任何程序,都会首先思考如何设计一个类。后面的遗传算法和CSP最小冲突算法,我也是封装到类中,这两个算法有点意思~
遗传算法,看似有些神秘,是一中对大自然“物竞天择,适者生存”法则的模拟。我仔细揣摩课本上面的思路,依葫芦画瓢写了一个程序,但是按照课本《人工智能:一种现代的方法》上面的写的算法只能算到10皇后。超过10皇后之后,就无法求出解。我通过调试,发现种群会慢慢收敛都一个局部最优解,“陷入泥淖,无法自拔”了。我发现,优质的个体(一个棋盘的状态)有时候无法被选中,从而“断子绝孙”。那么我就想办法拉开优质个体和劣质个体被选中几率的差距。慢慢的,我就想出了一个方法。改进过后,不仅解决8,10皇后时间缩短了大约85%(遗传的代数也减少85%),更是可以在较短时间内解决几十皇后的问题,比如40皇后。我是十分兴奋!期间我不断调整种群数量的大小,杂交的策略,还有变异的概率,逐渐发现了最优的参数。遗传算法可以继续优化,可以求解出几百皇后,不过我到了求解四十几皇后就没有继续优化了,已经可以较好完成作业的任务了。
再谈CSP(最小冲突),这是一种局部搜索。这对于求解对求解N皇后问题这样的constraint satisfy problem很有效果。这里的约束,就是指“皇后之间不能冲突”。该算法使用完全状态的形式化,不考虑过程。该算法最精彩的地方,是时间复杂度可以优化到O(n^2)(以付出一点空间复杂度为代价),于是可以在几秒内解决1万皇后的问题,在几十分钟内解决几万甚至10万皇后的问题!当我看到我的程序成功解决了10万皇后的那一刹那,内心简直是无比畅快,所有的努力和汗水都值得了
7 源代码
完整代码请在这里下载:N皇后C++完整源代码,采用面向对象思想设计 对照伪代码,看源代码,效果更佳!
友情提示:需要2个下载积分~(2个积分不多不多,尊重劳动成果~首次注册CSDN账户赠送50个积分~)。下面仅仅给出类的声明~
class NQueensBacktrack
{
public:
NQueensBacktrack():m_queens(0), m_counter(0), m_succussFindOne(false){};
NQueensBacktrack(int n) :m_queens(n, 0), m_counter(0){};
bool Check(int row, int column);
void Backtrack(int row);
void Print();
private:
vector<int> m_queens;
int m_counter;
bool m_succussFindOne;
};
class Genetic
{
public:
Genetic(int numOfQueens, int initialGroupNum);
double CalcuAdaptive(vector<int> &state); // 计算适应值(互相攻击的皇后对的个数的倒数)
void SetPopulation();
void Select(); // 选择
void Crossover(); // 杂交
void Crossover2(); // 另外一种杂交策略,和crossover()相比,优化了20%
void Mutate(); // 变异
void GeneticAlgorithm(); //把所有步骤综合在一起
void Print(); // 打印最优解
private:
size_t m_QueenNum; // 皇后数量
size_t m_BestAdaptive; // 最优解的适应值
bool m_NotSuccess; // 是否成功找到最优解
vector<int> m_BestOne; // 最优解
vector<vector<int>> m_population; // 种群
vector<double> m_adaptive; // 种群的适应值 --> 冲突对数的倒数
vector<double> m_accumuAdaptive; // 累积的适应值
//上述三个vector的下标之间是对应的(可理解为关联的)
};
class MinConflict
{
public:
MinConflict(int numOfQueens);
bool CheckSatus(); // 检测是否达到最优解
int CalcuConflicts(size_t row, size_t column);
void MinConflictAlgorithm();
void PutQueen(size_t row, size_t column);
void RemoveQueen(size_t row, size_t column);
void Print(); // 打印最优解
void PrintConflict();
private:
vector<int> m_chessBoard;
size_t m_QueenNum;
vector<int> m_columnConflict;
vector<int> m_mainDiaConflict; // 主对角线方向的映射规则 (i, j) --> m_QueenNum-1-i + j
vector<int> m_counterDiaConflict; // 映射规则 (i, j) --> m_QueenNum-1-i + m_QueenNum-1-j
};