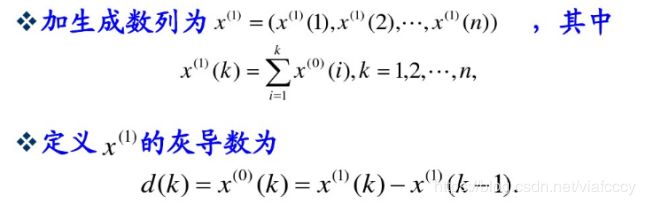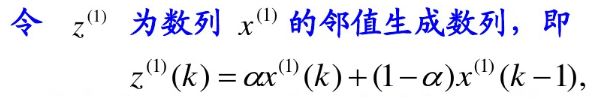GM(灰度预测模型)
根据某市1-6月的交通事故数量,建立灰色模型预测GM(1,1)(G表示grey,M表示model)预测7.8月份的交通事故数量(要求做精度检验)
灰色预测的概念
(1)灰色系统、白色系统和黑色系统
白色系统是指一个系统的内部特征是完全已知的,既系统信息是完全充分的。
黑色系统是一个系统的内部信息对外界来说是一无所知的,只能通过它与外界的联系来加以观测研究。
灰色系统介于白色和黑色之间,灰色系统内的一部分信息是已知的,另一部分信息是未知的,系统内各因素间有不确定的关系。
(2)灰色预测法
灰色预测法是一种预测灰色系统的预测方法。
灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。
原始数据
| 月份 |
1 |
2 |
3 |
4 |
5 |
6 |
| 事故数量 |
83 |
95 |
130 |
141 |
156 |
185 |
使用matlab将原始数据的直观图像绘制出来
line([1,2,3,4,5,6],[83,95,130,141,156,185],'Marker','o');
观察能够发现月份关于交通事故的数量为递增增长,离散分布在一个一次函数附近。
1.将原始数据写入矩阵
A = [83,95,130,141,156,185];
2.原数据进行处理从而弱化随机序列的波动性和随机性,对数据进行降噪。
一般处理的方法有累加(AGO),累减(IAGO),邻值加权,一次或多次级比(数列错位相除),对数变化等处理后使数据表现出明显的规律和趋势。对于这个原始数据来说直接使用累加就可以达到使数据的规律和趋势更加明显的作用。累加生成能使任意非负数列、摆动的与非摆动的,转化为非减的、递增的。
B = cumsum(A);
我们可以看累加后的数据图像
A = [83,95,130,141,156,185];
B = cumsum(A);
line([1,2,3,4,5,6],B,'Marker','o');
一次函数趋势更加明显,也就体现了累加的意义。同样适用其他处理方法的意义也在于此处。
3.求新生成数列的灰导数方程
不知道灰导数是什么没关系,先来看一下灰导数的求法就明白了但是此时要记住这个数列是我们累加后的数列。
灰导数其实就是相邻两项数据的差值,这也就体现了我们为什么一定要将原始数据处理成为一个一次函数趋势明显的数列。所以也可以看出来其实在整个灰度预测中怎样将原始数据处理成为一次函数趋势明显的数列是灰色模型的核心之一。也就是说我们如果不能消除突变或者灾变数据也就不适合使用灰色模型。
4.求数列的紧邻均值
这一步骤是进一步为灰微分方程的建立打下基础,是灰微分方程更加健壮。
5.建立GM(1,1)灰微分方程(一般的凡是表示未知函数、未知函数的导数与自变量之间的关系的方程,叫做微分方程。表达式:)
于是定义GM(1,1)的灰微分方程模型为d(k)+az(1)(k)=b或x(0)(k)+az(1)(k)=b
其实也就是d(x)=k z(1)(x)+b(y=kx+b)
其中,x(0)(k)x(0)(k)称为灰导数,a称为发展系数,z(1)(k)称为白化背景值,b称为灰作用量。
这步可以看到我们求紧邻均值的作用,使用均值来平滑数列的突变。
下面就将这个问题转换为知道一组数据就回归方程的问题(只不过这组数据被我们处理后变得一次函数趋势及其明显),我们用高中的最小二乘法求出a,b的数值。
for i=1:(n-1)
C(i) = (B(i)+B(i+1))/2;
end
6.白化GM(1,1)模型
我们此时得到的数据是离散状态的散点图,但是想要已知一个月份得到交通事故的数量,需要将这个灰色模型白化,得到确切的关系式从而计算结果。所以白化过程就是由离散回归连续的过程,但是这期间可能信息对等,也可能增加伪信息,这便是灰色模型成为灰色的一个原因。
7.求解模型
此时将离散方程转化为连续方程后d(k)不再是一个简单的差量,而被取了极限变为了微分,我们使用不定积分将函数的最终表达式求出。
这里我们只需要将我们的微分积分转化为下面的微分方程的形式然后求解即可。
8.模型检验
9.模型的预测
由于灰度模型适用范围有限,所以我们在以后适用GM时可以先使用下面的方法对模型进行简单的估计,如果满足条件就可以使用GM求解。
Λ(k)=x(0)(k-1)/x(0)(k)【这个式子称为级比】 若Λ(k)落在((e)^(-2/n+1),(e)^ (2/n+1))便适合使用GM求解。
10.预测结果
| 月份 |
1 |
2 |
3 |
4 |
5 |
6 |
| 结果 |
83.0000 |
103.7144 |
119.7793 |
138.3327 |
159.7598 |
184.5059 |
| 月份 |
7 |
8 |
9 |
10 |
11 |
12 |
| 结果 |
213.0851 |
246.0911 |
284.2096 |
328.2325 |
437.7914 |
379.0744 |
源代码:
clear
syms a b;
c = [a b]';
A = [83,95,130,141,156,185]; %将数据写入一维数组
n = length(A);
B = cumsum(A); %将A中的数据累加
for i=1:(n-1)
C(i) = (B(i)+B(i+1))/2; %求紧邻均值并且生成累加矩阵
end
%计算a,b参数
D=A;D(1)=[];
D=D';
E=[-C;ones(1,n-1)];
c=inv(E*E')*E*D;
c=c';
a=c(1);b=c(2);
%预测后续数据
F=[];F(1)=A(1);
for i=2:(n+6)
F(i)=(A(1)-b/a)/exp(a*(i-1))+b/a; %算出不定积分结果将F算出
end
G=[];G(1)=A(1);
for i=2:(n+6)
G(i)=F(i)-F(i-1); %累减还原
end
t1=1:6;
t2=1:12;
G
plot(t1,A,'o',t2,G)