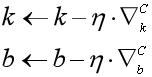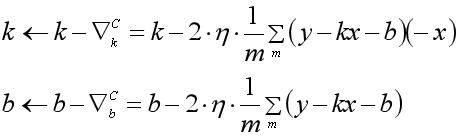Deeplearning4j 实战 （11）：基于Nd4j的线性回归模型的实现

Eclipse Deeplearning4j GitChat课程：https://gitbook.cn/gitchat/column/5bfb6741ae0e5f436e35cd9f
Eclipse Deeplearning4j 系列博客：https://blog.csdn.net/wangongxi
Eclipse Deeplearning4j Github：https://github.com/eclipse/deeplearning4j

Nd4j是Deeplearning4j生态圈中用于张量计算的一个子项目，其中张量的常见运算（标量的加减乘除，张量间的加减乘除以及Hadmard乘积等）都通过JavaCPP技术在off-heap memory上进行计算，可以选择的后台计算框架有：OpenBLAS，MKL等，这在之前的博客中也做过详细的分析，这里就不再赘述。其实无论是深度神经网络还是其他机器学习模型都需要有高效、专业的张量运算库来支持相关的数值计算。张量运算库从某种程度上是独立的一个功能模块。这里，我们就暂时抛开深度学习的相关内容，基于Nd4j来实现一种简单的机器学习模型--线性回归。一方面进一步说明Nd4j相关接口的应用方法以及一些可能的坑，再者梳理下利用已有张量计算库开发自己的算法模型的过程，供需要的同学参考。

首先我们说明下一元线性回归问题的相关概念。从机器学习的角度看，这个模型只存在单个维度的特征。并且模型的形式是：

其中k和b是仅有的两个需要学习的参数。我们的目的，就是通过已有的带有标注的训练数据，确定这两个参数的值，从而确定整个函数表达式或者说模型。

模型的形式非常简单和直观。接下来，我们需要定义损失函数。这里，我们用回归分析中最常见的均方误差函数（MSE）作为损失函数。即损失函数的形式为：

定义完损失函数之后，我们可以选择经典的梯度下降算法对损失函数进行优化计算。下面是分别基于全量的梯度下降和随机梯度下降法的参数迭代更新公式：

对于全量数据的梯度下降（Batch Gradient Descent，BGD）

对于随机梯度下降（Stochastic Gradient Descent，SGD）

从迭代公式可以看到，梯度下降的训练过程需要做大量的矩阵的加减乘除运算。BGD是每一次迭代都先计算出全量数据梯度的累加和并求取平均，再更新参数。而SGD的做法，则是对于每一条数据，都要更新一遍参数。下面，就梯度下降算法中需要用到的一些矩阵运算，给出Nd4j的实现：

首先给出pom文件中需要加入的依赖：

 

  
    UTF-8
    0.8.0
  	0.8.0
  	0.8.0
  	2.11
  
  
 
	   
	     org.nd4j
	     nd4j-native 
	     ${nd4j.version}
	   
	   
       junit
       junit
       4.12
     
 

 

张量（tensor）与标量（scalar）相加：

 

    @Test
    public void add(){
        INDArray data = Nd4j.create(new double[]{1.0,2.0});
        System.out.println(data.add(10.0));
        System.out.println(data);
    }

运行结果：

 

[11.00, 12.00]
[1.00, 2.00]

张量乘以标量：

 

    @Test
    public void mul(){
        INDArray data = Nd4j.create(new double[]{1.0,2.0});
        System.out.println("mul result: " + data.mul(20.0));
        System.out.println("after mul result: " + data);
        INDArray data2 = Nd4j.create(new double[]{1.0,2.0});
        System.out.println("muli result: " + data.muli(data2));
        System.out.println("after muli result: " + data);
    }

运行结果：

 

[20.00, 40.00]
[1.00, 2.00]

张量与张量对应位置的乘积（hadamard product）：

 

    @Test
    public void muli(){
        INDArray data1 = Nd4j.create(new double[]{1.0,2.0});
        INDArray data2 = Nd4j.create(new double[]{1.0,2.0});
        System.out.println(data1.muli(data2));
        System.out.println(data1);
        System.out.println(data2);
    }

运行结果：

 

[1.00, 4.00]
[1.00, 4.00]
[1.00, 2.00]

注意：这里有个隐藏的坑。如果直接调用INDArray的muli接口（也就是进行hadamard乘积运算），运算后会更新被乘的张量。比如上述逻辑中，data1这个向量的值最后是会被更新的，而不是保留原有值。这点非常重要！

 

张量除以标量：

 

    @Test
    public void div(){
        INDArray data = Nd4j.create(new double[]{1.0,2.0});
        System.out.println(data.div(2.0));
    }

运行结果：

 

[0.50, 1.00]

张量减去标量：

 

    @Test
    public void sub(){
        INDArray data = Nd4j.create(new double[]{1.0,2.0});
        System.out.println(data.sub(2.0));
    }

运行结果：

 

[-1.00, 0.00]

张量所有元素求和：

 

    @Test
    public void sum(){
        INDArray data = Nd4j.create(new double[]{1.0,2.0});
        System.out.println(data.sumNumber());
        System.out.println(Nd4j.sum(data));
    }

运行结果：

 

3.0
3.00

到此就基本罗列了开发梯度下降所需要的张量运算。下面就给出一元线性回归基于Nd4j的完整实现逻辑：

 

public class LinearRegression {
    private double learningrate = 0.1d;
    private double k;
    private double b;
    
    public LinearRegression(double k, double b, double learningrate){
        this.k = k;
        this.b = b;
        this.learningrate = learningrate;
    }
    
    public LinearRegression(double k, double b){
        this.k = k;
        this.b = b;
    }
    
    public double fitBGD(INDArray trainData, INDArray labelData){
        INDArray diff = labelData.sub(trainData.mul(k).add(b));
        k = diff.dup().muli(trainData).sumNumber().doubleValue() / trainData.length() * 2.0 * learningrate + k;
        b = diff.sumNumber().doubleValue() / trainData.length() * 2.0 * learningrate + b;
        return Nd4j.sum(diff.muli(diff)).div(trainData.length()).getDouble(0);
    }
    
    public double fitSGD(INDArray trainData, INDArray labelData){
        double diff = 0.0;
        for( int index = 0; index < trainData.length(); ++index ){
            double label = labelData.getDouble(index);
            double data = trainData.getDouble(index);
            diff = label - (k * data + b);
            k = k + 2 * diff * data * learningrate;
            b = b + 2 * diff * learningrate;
        }
        return diff * diff;
    }
    
    public double getK(){
        return k;
    }
    
    public double getB(){
        return b;
    }
}

这里解释下一元线性回归模型的实现。
1.就像在文章开始说的那样，一元线性回归有k,b两个参数，并且它们都是标量。
2.通过构造函数，我们可以传入k，b的初始值，此外学习率也可以设定（学习率一般的取值有：0.1，0.01，0.001等）

3.这里不考虑L1/L2正则化的惩罚项

4.训练的办法有BGD和SGD两种。可以任意选择。两种训练方法的差别上面的内容已经有所叙述。

紧接着，给出测试案例以及训练结果：

 

    public static void main(String[] args){
        LinearRegression model = new LinearRegression(0.1 , 0.1);
        double k_label = 125.6;
        double b_label = 10.3;
        INDArray data = Nd4j.getRandom().nextDouble(new int[]{1,1000});
        INDArray label = data.mul(k_label).add(b_label);
        final int iterations = 1;
        for( int iter = 0; iter < iterations; ++iter ){
            double loss = model.fitSGD(data, label);
            System.out.println(loss);
        }
        System.out.println("k: " + model.getK());
        System.out.println("b: " + model.getB());
    }

这段测试代码的目的在于拟合我们人为设定的一个线性回归函数：y=125.6x+10.3。

训练数据为了简便起见，直接通过随机数生成器生成，也就是逻辑中的data变量，一共有1000条训练数据，它们的标注值是变量label。

这段逻辑是调用了SGD算法进行模型拟合。训练过程中，我们会把损失函数的值打印出来。训练过程如下：

 

1367.039131683817
3589.697743185614
814.9340052568914
0.6982890684168035
9003.192518775708
2973.690456554632
249.23938735916659
750.52925264099
1282.4124017181582
......
7.99018909956992E-10
3.2702298931377578E-9
2.2272485481616583E-8
5.705757093487267E-9
2.3704678972317464E-10
4.023154132945466E-9
1.554740048190016E-9
5.813383195642535E-11
1.0528857055403527E-8
1.6685435061096738E-8
2.8577651355978647E-9
2.8577651355978647E-9
k: 125.59969241550412
b: 10.300193487367387

可以看到，模型最后收敛的结果是：k=125.599，b=10.300，和我们人为设定的结果几乎一致。

我们再用BGD的方式来训练模型：

 

    public double fitBGD(INDArray trainData, INDArray labelData){
        INDArray diff = labelData.sub(trainData.mul(k).add(b));
        k = diff.dup().muli(trainData).sumNumber().doubleValue() / trainData.length() * 2.0 * learningrate + k;
        b = diff.sumNumber().doubleValue() / trainData.length() * 2.0 * learningrate + b;
        return Nd4j.sum(diff.muli(diff)).div(trainData.length()).getDouble(0);
    }

训练的结果是：

 

6683.94384765625
4031.71435546875
2547.056640625
1712.5667724609375
1240.216552734375
969.666259765625
811.6519775390625
......
0.0013102099765092134
0.0012754499912261963
0.0012416469398885965
0.0012087703216820955
0.0011767115211114287
0.0011454694904386997
0.001115068793296814
k: 125.48767310171132
b: 10.36036205997471

用BGD进行训练的时候，损失函数一直在不断下降，并没有像SGD那样发生振荡的情况。最后收敛的情况也比较理想。

 

到此，基于Nd4j构建的一元线性回归模型的实现就基本完成了。下面做下简单的总结：

Nd4j是一个基于JVM的，接口和numpy接近的张量运算库。它可以切换底层计算的实际后端，比如：OpenBLAS或MKL。其本身虽然是深度学习开源库：Deeplearning4j的一个依赖模块，但可以在其上独立开发其他经典算法模型。这篇文章的内容旨在让有兴趣的同学了解Nd4j中常用的运算接口，同时结合简单清晰的一元线性回归模型为例，给出了基于Nd4j的实现方案。希望对Nd4j基础上做二次开发的同学有所帮助和借鉴。