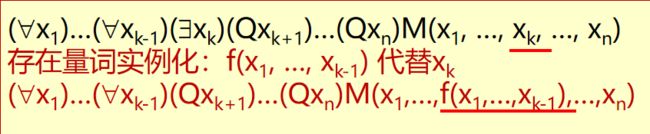人工智能(一种现代的方法)(第三版)(学习笔记)(前七章)
人工智能(一种现代的方法)(第三版)(学习笔记)
- 第一部分 人工智能
- 第1章 绪论
- 第2章 智能 Agent
- Agent通过传感器感知环境并通过执行器对所处环境产生影响。
- 理性Agent的定义
- 理性的判断依赖
- 理性与全知的区别
- 理性Agent的两大特点
- 任务环境(PEAS描述)
- 任务环境的性质
- Agent的结构
- 基本的Agent程序
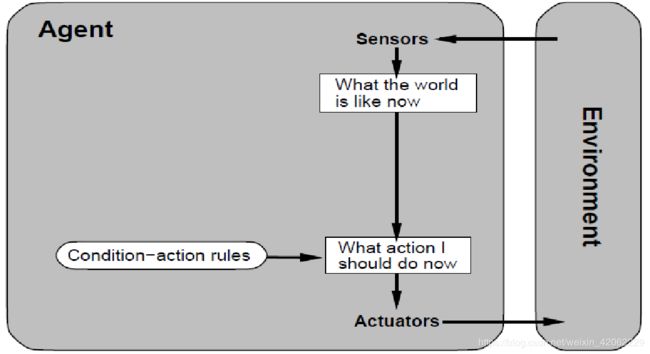
- 简单反射Agent
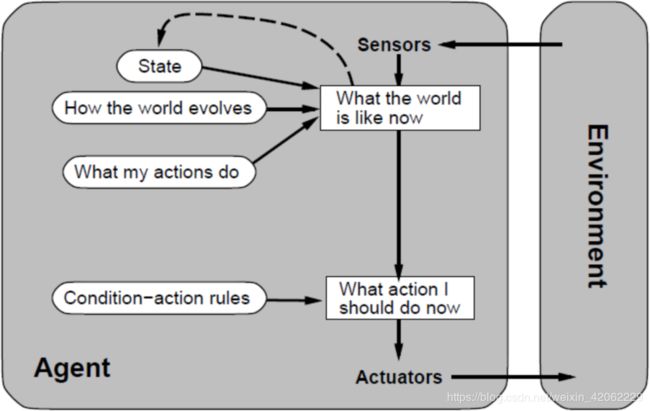
- 基于模型的反射Agent
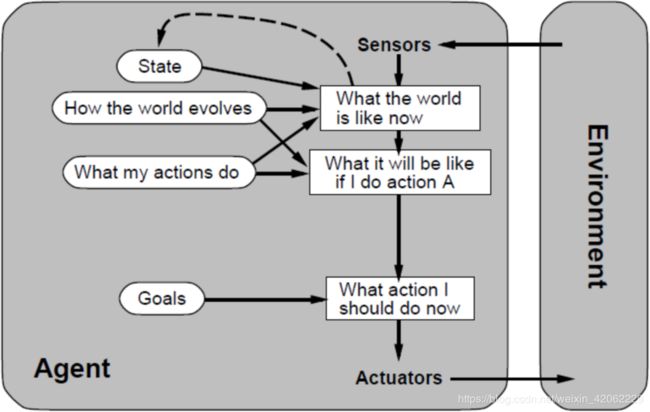
- 基于目标的Agent
- 基于效用的Agent
- 学习Agent(4个组件)
- Agent的工作逻辑
- 课后习题
- 2.2
- 2.3
- 第二部分 问题解决
- 第3章 通过搜索进行问题求解
- 问题求解Agent
- 罗马尼亚案例的PEAS
- 真空吸尘器世界的问题形式化
- 八数码问题的问题形式化
- 八皇后问题
- 通过搜索求解
- 树搜索
- 图搜索
- 无信息搜索策略
- 宽度优先搜索 (BFS)
- 一致代价搜索 (Uniform-cost Search)
- 深度优先搜索(DFS)
- 深度受限搜索(Depth-limited Search)
- 迭代加深的深度优先搜索(Iterative Deepening Search)
- 双向搜索(Bidirectional Search)
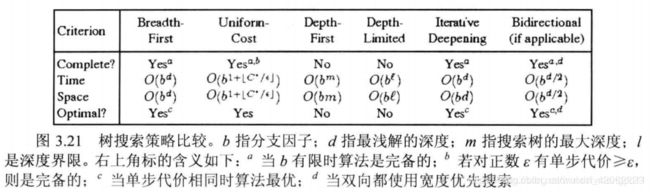
- 对比
- 有信息(启发性)搜索
- 贪婪最佳优先搜索(Greedy Best-first Search)
- A*算法
- 存储受限的启发式搜索:RBFS和MA*
- 学习(以促)搜索
- 启发式函数
- 课后习题
- 3.1
- 3.2
- 3.6
- 第4章 超越经典搜索
- 4.1局部搜索和最优问题
- 爬山算法
- 模拟退火
- 局部束搜索
- 遗传算法
- 对比
- 4.2连续空间的局部搜索
- 4.3 使用不确定动作的搜索
- 4.4 使用部分可观察信息的搜索
- 第5章 对抗搜索
- 5.1博弈
- 5.2博弈中的优化决策
- 5.2.1极小极大算法
- 5.2.2多人博弈时的最优决策
- 5.3α-β剪枝
- 5.3.1行棋排序
- 5.4不完美的实时决策
- 5.4.1评估函数
- 5.4.2截断搜索
- 5.4.3向前剪枝
- 第六章 约束满足问题
- 第七章 逻辑Agents
- 7.2 逻辑
- 7.3 命题逻辑:一种简单的逻辑
- 7.4 命题逻辑定理证明
- 一阶逻辑表示
- 一阶逻辑的推理
欢迎大家提出需要详细写的地方!欢迎纠正!
第一部分 人工智能
第1章 绪论
名词解释(中英可能不一致):
(1)智能:应用知识以便在环境中更好地使用知识的能力。
the ability to apply knowledge in order to perfrom better in an environment.
(2)人工智能:
是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。
针对给定的代理架构在给定环境中表现良好的代理程序的研究和构建。
the study and construction of agent programs that perform well in a given environment, for a given agent architecture.
(3)Agent:对环境中的感知作出反应而采取行动的实体。
an entity that takes action in response to percepts from an environment.
(4)理性:所知道的“正确的东西”的特性。
the property of a system which does the “right thing” given what it knows.
(5)逻辑推理:从旧句子中导出新句子的过程,这样如果旧句子是真实的,那么新句子就必然是真实的。
the a process of deriving new sentences from old, such that the new sentences are necessarily true if the old ones are true.
1.3 缩手是理性的,因为缓慢、慎重的行动往往会导致手受到更大的伤害。如果“智能”意味着“应用知识”或“使用思想和推理”,那么它就是。 我们不需要智力来做出反应。
第2章 智能 Agent
Agent通过传感器感知环境并通过执行器对所处环境产生影响。
AI的任务是设计Agent程序,实现把感知信息映射到行动的Agent函数。
Agent就是能够行动的某种东西,具备自主的操作、感知环境、长期持续、适应变化并能创建与追求目标。
Agent的感知序列:是该Agent所受到的所有输入数据的完整历史。
Agent函数:描述了Agent的行动,它将任意给定感知序列映射为行动。
Agent函数是抽象的数学描述,Agent程序是具体实现
Agent函数与Agent程序的区别(判断题)
-
每个Agent函数都可以程序/机器组合实现
错。受机器的运行速度和存储能力所限。 -
一个Agent函数可能对应多个Agent程序
对。Agent程序与运行平台关联。
理性Agent的定义
理性Agent:基于已知信息以追求最大化目标收益
对每一个可能的感知序列,根据已知的感知序列提供的证据和Agent具有的先验知识,理性Agent应该选择能使其性能度量最大化的行动。
理性的判断依赖
- 定义成功标准的性能度量
- Agent对环境的先验知识
- Agent可以完成的行动
- Agent截止到此时的感知序列
练习:什么是理性
一个理性的打牌Agent不可能输
错。理性的打牌Agent是在已知牌面的情况下输得最少
一个Agent只能感知状态的部分信息,那么不可能是理性的
错。理性不等于全知。
理性与全知的区别
一个全知的Agent明确的知道它的行动产生的实际结果并且做出相应的动作。全知者在现实中是不可能的。
理性是使期望的性能最大化,而完美是使实际的性能最大化。对Agent而言,完美是不太合理的要求。
理性并不要求全知。理性的选择只依赖于到当时为止的感知序列。
理性Agent的两大特点
- 信息收集 ,观察有助于期望性能的最大化。
- 自主学习 ,从所感知的信息中尽可能多的学习,以弥补不完整的或者不正确的先验知识。
理性Agent 理性不等于成功 理性不等于全知,更不等于可以不知, 理性意味着探索、学习、自主
任务环境(PEAS描述)
Performance性能
Environment环境
Actuators执行器
Sensors传感器
设计Agent的第一步:尽可能完整地详细说明任务环境。
任务环境的性质
完全可观察的 vs 部分可观察的
- 如果Agent的传感器在每个时间节点上都能获取环境的完整状态,这个任务环境就是完全可观察的。否则,则是部分可观察的。
- 如果传感器能够检测所有与行动决策相关的信息,该任务环境就是有效完全可观察的。
- 如果Agent根本没有传感器,环境则是无法观察的。
单Agent vs 多Agent
- 区分两者的关键在于Agent B 行为的性能度量最大化是否需要依赖于Agent A的行为。
- 竞争性的多Agent环境
Agent B想要最大化自己的性能度量,就需要最小化Agent A的性能度量。(国际象棋) - 合作性的多Agent环境
Agent B想要最大化自己的性能度量,就需要最大化Agent A的性能度量。(车辆驾驶) - 部分合作部分竞争的多Agent环境 (随机行为是理性的,这样可以避免预测中的缺陷)
确定的 vs 随机的
- 如果环境的下一个状态完全取决于当前状态和Agent执行的动作,则该环境是确定的;否则,是随机的。
- 不确定与随机的区别
环境不确定是指环境不是完全可观察的或不确定的,行动后果可能有多种,但与概率无关。
环境随机是指后果是不确定的并且可以用概率来量化。
片段式 vs 延续式
- 片段式是指当前决策不会影响到未来的决策。
- 延续式是指当前决策会影响到所有未来的决策。
静态 vs 动态
- 如果环境在Agent计算的时候会变化,该环境是动态的,否则是静态的。
- 如果环境本身不随时间变化而变化,但Agent的性能评价随时间变化,则环境是半动态的。
离线 vs 连续
使用场景:
- 环境的状态
- 时间的处理方式
- Agent的感知信息和行动
已知 vs 未知
- 指的是Agent的知识状态。
如果环境是未知的,Agent需要学习环境是如何工作的,以便做出好的决策。
最难处理的情况
- 部分可观察的、多Agent的、随机的、延续的、动态的、连续的和未知的环境。
Agent的结构
Agent = 体系结构 (某个具备物理传感器和执行器的计算装置)+ 程序。
基本的Agent程序
简单反射Agent
方法
Step 1:首先构建一个通用的条件-行为规则解释器。
Step 2:根据特定任务环境创建相应的规则集合。
简单反射Agent中的问题
- 规则构建与存储困难
- 规则冲突
- 不能存储历史信息(无限循环)
- 不能处理世界的随机性、变化性
缺点 :在部分可观察环境中运转的简单反射Agent经常不可避免地陷入无限循环中。
解决办法:行动随机化
基于模型的反射Agent
-
使用世界模型的Agent称为基于模型的Agent
-
Agent应该根据感知历史维持内部状态,从而至少反映出当前状态看不到的信息。部分可观察、动态的、片段式的。
-
随时更新内部状态信息要求在Agent程序中加入两种类型的知识:
世界模型:
知识一:世界是如何独立于Agent而发展的信息
知识二:Agent自身的行动如何影响世界 -
缺点 :部分可观察环境中的Agent不能精准确定当前状态
自动驾驶出租车的PEAS
Performance measure: 遵守交通规则,安全驾驶
Environment:有车的公路
Actuator: 停车、加速、减速、转弯
Sensors: 摄像头、红外、车轮解码器等
世界是如何独立于Agent而发展的信息:周围车辆在减速、加速、转弯、超车;移动的行人。
基于目标的Agent
-
既跟踪记录世界的状态,也记录它要达到的目标集合,并选择能(最终)导致目标达成的行动
-
特点 :
-
主要用在搜索和规划问题中:Agent 需要一个目标来了解期望达到什么状况
随着达到目标所需要的动作数目的增多,问题越来越难求解 -
虽然显得效率较低,但更灵活。因为支持它决策的知识被显示表现出来,且可以修改。
-
部分可观察、动态的、连续式的
- 不适用的情况
多个目标互相冲突
有几个目标,但没有一个有把握达到
这两种情况,通过效用Agent可以解决
自动驾驶出租车的PEAS
P: 遵守交通规则,安全驾驶,能够到达指定地点
E: 有车的公路
A: 停车、加速、减速、转弯
S: 摄像头、红外、车轮解码器等
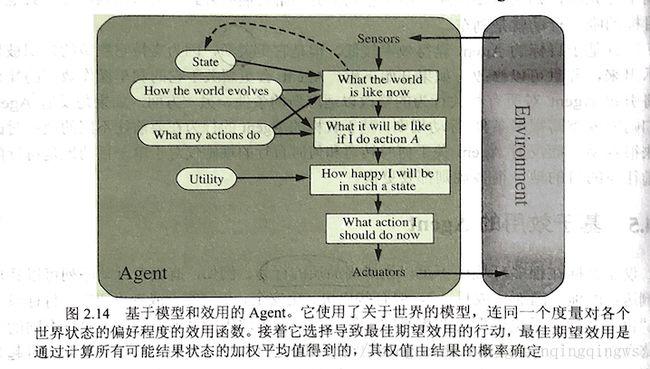
基于效用的Agent
-
理性的基于效用的Agent:选择期望效用最大化的行动,Agent在给定每个结果的概率和效用下,期望得到的平均效用。
-
Agent的效用函数是性能度量的内在化。实际实现时因为计算复杂性而不可能完美达成。
-
方法
Step 1:使用关于世界的模型,以及对各个世界状态的偏好程度进行度量的效用函数。
Step 2:选择可以取得最佳期望效用的行动。
Step 3:通过结果的概率来确定权值,最佳期望效用是通过计算所有可能结果状态的加权平均值得到的。 -
适用情况
1、当多个目标互相冲突时,只有其中一些目标可以达到时,效用函数可以在它们之间适当的折中。
2、当Agent有几个目标,但没有一个有把握达到时,效用函数可以在它们之间适当的折中。
学习Agent(4个组件)
- 学习元件
负责改进提高,利用来自评判元件的反馈评价Agent做得如何,并确定应该如何修改性能元件以便将来做得更好。
- 性能元件
接受感知信息并决策。
- 评判元件
根据固定的性能标准告诉学习元件Agent的运转情况。
- 问题产生器
建议探索性行动,负责可以得到新的和有信息的经验的行动建议。
Agent的工作逻辑
![]()
-
原子表示
没有内部结构的表示。
相关内容:搜索、博弈论、隐马尔可夫模型、马尔可夫决策过程。
-
要素化表示
一个状态中包含多个要素(原子),即多个变量和特征的集合。
相关内容:约束满足算法、命题逻辑、规划、Bayesian网、机器学习算法。
-
结构化表示
一个状态包含对象、每个对象可能有自身的特征值,以及与其他对象的关系。
相关内容:关系数据库、一阶逻辑、一阶概率模型、基于知识的学习、自然语言理解。
- 所有Agent都可以通过学习来改进它们的性能
课后习题
2.2



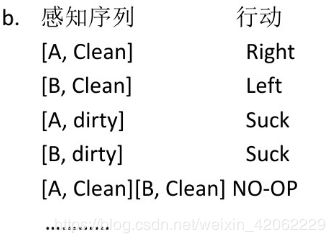

c. 讨论在干净的方格可能变脏和环境地理不明的情况下可能的Agent设计。在这种情况下Agent从经验中学习有意义吗?若果有,该学习什么?如果没有意义,为什么?
答:在干净的方格可能变脏的情况下,可采用不定期检查并清理变脏的地方;在环境地理不明的情况下,通过学习地理信息,可以优化Agent的路径,Agent可通过学习掌握某地方变脏的分布情况。
2.3
- A. 只感知有关状态的部分信息的代理不能是完美理性的。 假的。完美理性是指考虑到传感器信息而做出正确决策的能力。
- B. 存在没有完全反应agent能合理反应的任务环境。
是的。完全反应agent忽略了以前的感知,因此不能在部分可观测的环境中获得最优状态估计。例如,对应象棋是通过发送动作来进行的;如果另一个玩家的动作是当前的知觉,则反射agent无法跟踪棋盘状态,因此无论它在哪个位置进行,都必须以相同的方式对“A4”做出响应。
第二部分 问题解决
第3章 通过搜索进行问题求解
问题求解Agent
问题形式化:(以罗马尼亚案例为例说明)
-
初始状态: In(Arad)
-
行动:ACTIONS(s),即,给定一个状态s,ACTIONS(s)返回状态s下可以执行的动作的集合。例如状态s为 *In(Arad),动作集合( { Go(Sibiu) , Go(Timisoara) , Go(Zerind)} )
-
转移模型:RESULT(s,a),在状态s下,执行a动作后,达到的状态。也会使用后继状态表示从一给定状态出发,通过单步行动,可以达到的状态集合。例如
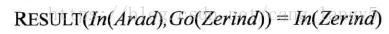
-
目标测试:确定给定的状态是不是目标状态。
有时,目标状态是一个显示集合(已知的,明确的),测试只需要简单的检查给定状态是否在目标状态集合中。例如已知的目的地。
有时,目标状态不是一个显式可枚举的目标状态集合,而是具备某些特定抽象属性的状态。例如,国际象棋中,目标状态是指被将死的状态,即,对方国王在己方国王攻击得无路可逃必死无疑。 -
路径耗散:路径耗散函数为每条路径赋一个耗散值,即,边加权,罗马尼亚案例中,路径耗散可以是用公里数表示的路径长度。采用行动a从状态s走到状态s’所需要的单步耗散用c(s, a, s’)。
问题的解,是从初始状态到目标状态的一组行动序列。
解的质量,由路径耗散函数衡量,路径耗散值最小的即为最优解。
初始状态、行动和转移模型定义了问题的状态空间,即,从初始状态可以达到的所有状态的集合。
罗马尼亚地图就可以解释为一个状态空间图,结点表示状态,结点之间的弧表示行动。状态空间中的一条路径指的是通过行动连接起来的一个状态序列。
罗马尼亚案例的PEAS
见第二章的环境任务的描述(这是第二章的内容)
(Performance性能 ,Environment环境,Actuators执行器,Sensors传感器)
-
可观察的:Agent总是知道当前状态,Agent在罗马尼亚开车,每到达一个城市通过观察访问标识,知道是否访问过该城市。
-
离散的:在任一给定状态,可选的行动是有限的,在罗马尼亚游玩时,每个城市只与有限个数城市相邻。
-
已知的:Agent知道每个行动达到的状态(地图显示)
-
确定的:每个行动的结果唯一可确定。
真空吸尘器世界的问题形式化
八数码问题的问题形式化
八皇后问题
这类问题的形式化分为两类:
-
增量形式化:从空状态开始,每次添加一个皇后。其形式化如下:
这是最笨的方法,盲目地行动:

思考:如果禁止把一个皇后放到可能被攻击的格子里,这样的形式化更好。

-
完整状态形式化
状态:八个皇后的任一摆放都是一个状态。
初始状态:8个皇后都在棋盘上。
行动:选择一个皇后移动。
转移模型: 将移动后的棋盘返回。
目标测试:八个皇后都在棋盘上,并且无法互相攻击。无论哪种情况,都不需要考虑路径消耗,只需考虑最终状态。
通过搜索求解
frontier:已生成未拓展
closed:已拓展
-
一个解是一个行动,搜索算法考虑各种可能的行动序列
STATE:空间中的状态。
PARENT:产生该节点的父节点
ACTION:父节点产生该节点的行动
PATH-COST:代价(路径耗散) -
问题求解算法的性能
完备性:是否保证能找到解
最优性:是否能找到最优解
时间复杂度:找到解需要多少时间
空间复杂度:搜索中需要多少内存
树搜索
图搜索
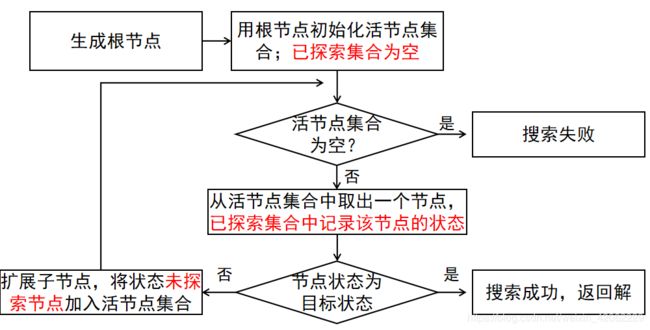
树搜索:重复状态增大时间开销,甚至导致死循环
图搜索:避免重复状态,空间开销大
无信息搜索策略
宽度优先搜索 (BFS)
- 基于节点深度的非递减函数,宽搜最优
- 扩展的是未扩展节点中深度最浅的节点
- 目标检测应用于被选择拓展时
- 时间复杂度:O(bd+1)
b = 一个非叶节点的子节点数
d = 层数
一致代价搜索 (Uniform-cost Search)
- 每一步的行动代价都相等时,BFS是最优的。
- 扩展的是路径消耗g(n)最小的结点。
- 目标检测应用于被选择拓展时
- 如果边缘中的节点有更好的路径到达该节点,则会引入一个测试。
- 不关心步数,只关心路径总代价。
- 当单步代价相同时,等价于宽度优先搜索
- 当单步代价为正时,算法是最优的
- 时空复杂性均为 O(b1+[cl ]),C 是最优解的代价
深度优先搜索(DFS)
-
扩展的是可扩展节点中深度最深的节点
-
目标检测应用于被选择拓展时
-
在有限状态空间中,DFS是完备的,因为它可以把所有空间遍历一遍;
-
而在无限空间中,DFS则有可能会进入深度无限的分支,因此是不完备的。
-
DFS的时间复杂度为为O(bd),而空间复杂度仅为O(d)
因为我们只需要保存当前分支的状态,因此空间复杂度远远好于BFS。然而DFS并不能保证找到最优解。
深度受限搜索(Depth-limited Search)
深度受限搜索设定一个最大深度dmax,当搜索深度大于dmax的时候立即回溯,从而避免了在无穷状态空间中陷入深度无限的分支。
迭代加深的深度优先搜索(Iterative Deepening Search)
迭代加深的深度有限搜索也设定一个最大深度dmax,开始我们把dmax设为1,然后进行深度受限搜索,如果么有找到答案,则让dmax加一,并再次进行深度有限搜索,以此类推直到找到目标。这样既可以避免陷入深度无限的分支,同时还可以找到深度最浅的目标解,从而在每一步代价一致的时候找到最优解,再加上其优越的空间复杂度,因此常常作为首选的无信息搜索策略。
双向搜索(Bidirectional Search)
分别从源头和目标搜索。
对比
性能指标
完备性:只要有一定能找到
最优性:能够找到最优解
复杂性:算法求解所需要耗费的时间与空间
有信息(启发性)搜索
最佳优先搜索的评价函数f(n) 由启发函数(heuristic function)构成
h(n) = 结点n到目标结点的最小代价路径的代价估计值
贪婪最佳优先搜索(Greedy Best-first Search)
使用启发式,f(n) = h(n)
距离目标最近,最快找到解
A*算法
缩小总体评估代价
f(n) = g(n) + h(n)
保证最优性
存储受限的启发式搜索:RBFS和MA*
略
迭代加深A*(截断值改成f(n))
递归最佳优先搜索RBFS(节点回退时将回退路径上的点写上最短的代价)
学习(以促)搜索
元状态空间中的每一个状态都要捕捉一个程序的内部状态,程序是在目标层状态空间搜索。元状态空间的每一个行动都是改变内部状态的计算步骤。
学习的目标时减小问题求解的总代价,计算开销和路径代价之间取得最佳性价比。
启发式函数
同问题有多种启发函数
启发式精确度对性能的影响。
有效分支因子b*,设总结点为N,解的深度为d,b*为深度为d的标准搜索树为了能包括N+1个点所必须的分支因子。即,N+1 = 1 + b^1 + b^2 + … +b^d
从松弛问题出发设计可采纳的启发式
减小了行动限制的问题称为松弛问题。松弛问题的状态空间图是原有状态空间的超图,因为减少限制导致图中边的增加。
从子问题出发设计可采纳的启发式——模式数据库
子问题的最优解代价是完整问题的解代价的下界。存储每一个子问题代价的实例,作为启发式用。两个不想叫的子问题的代价之和是整个问题的下界(不相交的模式数据库)
从经验中学习启发式,线性回归方程等。
课后习题
3.1
解释为什么问题的形式化要在目标的形式化之后。
答:在制定目标时,我们决定我们对世界的哪些方面感兴趣,哪些方面可以被忽视或抽象化。然后,在问题描述中,我们决定如何操纵重要的方面(而忽略其他方面)。如果我们先制定问题,我们就不知道应该包括什么,也不知道遗漏了什么。也就是说,在目标制定、问题制定和问题解决之间有一个循环,直到一个人找到一个足够有用和有效的解决方案。
3.2
你的目标是将机器人从迷宫中导航出去。机器人从迷宫中心开始朝北。您可以将机器人转到面向北、东、南或西。您可以指示机器人向前移动一定距离,尽管它在撞到墙壁之前会停止。
a.制定此问题。状态空间有多大?
b、在迷宫中,我们唯一需要转弯的地方是两个或多个走廊的交叉点。使用此观察重新格式化此问题。现在状态空间有多大?
c.从迷宫中的每一点开始,我们可以沿着四个方向中的任何一个方向移动,直到到达一个转折点,这是我们唯一需要做的动作。使用这些操作重新设置问题。我们现在需要追踪机器人的方向吗?
d在我们对我们已经从现实世界中提取的问题的初始描述中,限制操作和删除细节列出我们所做的三个这样的简化。
答案A.我们将定义坐标系,使得迷宫的中心位于(0,0),迷宫本身是(1,1)到(1,1)的正方形。
初始状态:机器人在坐标(0,0),面向北。
目标测试:X>1或Y>1,其中(x,y)为当前位置。
行动:向前移动任何距离D;将方向机器人改变方向。
成本函数:移动的总距离。由于机器人的位置是连续的,所以状态空间是无限大的。
答案B.将记录机器人目前的交叉口的状态,以及它面临的方向。在每条走廊的尽头,离开迷宫,我们将有一个出口节点。我们假设某个节点对应于迷宫的中心。
初始状态:位于朝北迷宫中心。
目标测试:在出口节点。
行动:如果有一个交叉口,就移到前面的下一个十字路口;转向一个新的方向。
成本函数:总移动距离。有4N个状态,其中n是交叉口的数目。
答案C.
初始状态:在迷宫的中心。
目标测试:在退出节点处。
行动:移动到北、南、东或西的下一个交叉点。
成本函数:移动的总距离。
我们不再需要跟踪机器人的方位,因为它与预测我们的行动的结果无关,而且不是目标测试的一部分。执行该计划的电机系统需要跟踪机器人的当前取向,以知道何时旋转机器人。
答案D.
状态抽象:(i)忽略机器人离地面的高度,不管它是否从垂直方向倾斜。
(ii)机器人只能在四个方向上面对。
(iii)世界的其他部分被忽略:其他机器人在迷宫中的可能性,天气等。
动作抽象:(i)我们假设我们可以安全访问的所有位置:机器人无法卡住或损坏。
(ii)机器人可以无电源限制地移动。
(iii)简化的移动系统:向前移动一定距离,而不是控制每个单独的马达并观看传感器以检测碰撞。
3.6
有三个水壶,容量分别为12加仑,8加仑,3加仑,还有一个放液嘴。可以吧水壶装满或倒空,从一个壶倒进另一个壶或倒在地上。请量出刚好1加仑水。
状态:(V(a),V(b),V©);V(a),V(b),V©是各壶中水的体积;V(a)⋲Z,0<=V(a)<=12;V(b)⋲Z,0<=V(b)<=8;V©⋲Z,0<=V©<=3;
初始状态:V(a)=V(b)=V©=0
行动:这个任务环境中,每个状态可执行的行动共有12种。分别为:将a中的水倒入b中;将a中的水倒入c中;a中的水倒在地上;将a装满;将b中的水倒入a中;将b中的水倒入c中;b中的水倒在地上;将b装满;将c中的水倒入a中;将c中的水倒入b中;将c中的水倒在地上;将c装满。
转移模型:(V’(a),V’(b),V’©) = result(V(a),V(b),V©,action)
其中V(a),V(b),V©是执行动作前各壶中水的体积,action为执行的动作,V’(a), V’(b), V’©是执行动作后各壶中水的体积。
对于不同action,result函数计算公式如下:
1.将a中的水倒入b中。V’(a)=V(a)-min(8-V(b),V(a));V’(b)=V(b)+min(8-V(b),V(a));V’©=V©
2.将a中的水倒入c中。V’(a)=V(a)-min(3-V©,V(a));V’(b)=V(b);V’©=V©+min(3-V©,V(a))
3.a中的水倒在地上。V’(a)=0;V’(b)=V(b);V’©=V©
4.将a装满。V’(a)=12;V’(b)=V(b);V’©=V©
5.将b中的水倒入a中。V’(a)=V(a)+min(12-V(a),V(b));V’(b)=V(b)-min(12-V(a),V(b));V’©=V©
6.将b中的水倒入c中。V’(a)=V(a);V’(b)=V(b)-min(3-V©,V(b));V’©=V©+min(3-V©,V(b))
7.将b中的水倒在地上。V’(a)=V(a);V’(b)=0;V’©=V©
8.将b装满。V’(a)=V(a);V’(b)=8;V’©=V©
9.将c中的水倒入a中。V’(a)=V(a)+min(12-V(a),V©);V’(b)=V(b);V’©=V©-min(12-V(a),V©);
10.将c中的水倒入b中。V’(a)=V(a);V’(b)=V(b)+min(8-V(b),V©);V’©=V©-min(8-V(b),V©)
11.将c中的水倒在地上。V’(a)=V(a);V’(b)=V(b);V’©=0
12.将c装满。V’(a)=V(a);V’(b)=V(b);V’©=3
目标测试:V(a)=1 or V(b)=1 or V©=1
路径消耗:每一步耗散值为1,整个解路径的耗散值是路径中的步数。
第4章 超越经典搜索
本章考虑对一个或多个状态进行评价和修改,而不是系统地搜索从初始状态开始的路径。也就是说,本章注重找到解状态,而忽略初始状态到解的路径。
推荐实验:八皇后问题和八数码问题的最陡上升爬山法、首选爬山法、随机重启爬山法、模拟退火算法的分析和实现
https://blog.csdn.net/weixin_40975029/article/details/88752215
4.1局部搜索和最优问题
局部搜索算法从单一当前节点出发,通常只移动到它的临近状态。
优点:内存消耗很小,适用于 系统算法不适用的 很大或无限的状态空间中 寻找合理的解。 状态空间地形图(见下),坐标(表示状态),高度(表示代价函数或目标函数)。如标高对应代价,最低谷即全局最小值。如标高对应目标函数,最高点即全局最优解。

爬山算法
- 首选爬山算法
依次寻找该点X的邻近点中首次出现的比点X价值高的点,并将该点作为爬山的点(此处说的价值高,在该题中是指Z或f(x,y)值较大). 依次循环,直至该点的邻近点中不再有比其大的点. 我们成为该点就是山的顶点,又称为最优点. - 最陡爬山算法
最陡爬山算法是在首选爬山算法上的一种改良,它规定每次选取邻近点价值最大的那个点作为爬上的点.
3.随机重启爬山算法
随机重新开始爬山算法是基于最陡爬山算法,其实就是加一个达到全局最优解的条件,如果满足该条件,就结束运算,反之则无限次重复运算最陡爬山算法.
容易出现的问题: 局部最大值
山脊,造成了一系列的局部极大值
高原,造成了一大块局部最大值,最速梯度下降会迷路
模拟退火
模拟退火其实也是一种贪心算法,但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解,这个概率随着时间推移逐渐降低(逐渐降低才能趋向稳定)因此有可能会跳出这个局部的最优解,达到全局的最优解。
模拟退火算法的优缺点模拟退火算法的应用很广泛,可以高效地求解NP完全问题,如货郎担问题(Travelling Salesman Problem,简记为TSP)、最大截问题(Max Cut Problem)、0-1背包问题(Zero One Knapsack Problem)、图着色问题(Graph Colouring Problem)等等,但其参数难以控制,不能保证一次就收敛到最优值,一般需要多次尝试才能获得(大部分情况下还是会陷入局部最优值)。观察模拟退火算法的过程,发现其主要存在如下三个参数问题:
(1) 温度T的初始值设置问题
温度T的初始值设置是影响模拟退火算法全局搜索性能的重要因素之一、初始温度高,则搜索到全局最优解的可能性大,但因此要花费大量的计算时间;反之,则可节约计算时间,但全局搜索性能可能受到影响。
(2) 退火速度问题,即每个T值的迭代次数
模拟退火算法的全局搜索性能也与退火速度密切相关。一般来说,同一温度下的“充分”搜索是相当必要的,但这也需要计算时间。循环次数增加必定带来计算开销的增大。
(3) 温度管理问题
温度管理问题也是模拟退火算法难以处理的问题之一。实际应用中,由于必须考虑计算复杂度的切实可行性等问题,常采用如下所示的降温方式:
T=α×T.α∈(0,1).
注:为了保证较大的搜索空间,α一般取接近于1的值,如0.95、0.9。
特点:
- 迭代搜索效率高,并且可以并行化
- 算法中有一定概率接受比当前解较差的解,因此一定程度上可以跳出局部最优算法求得的解
- 与初始解状态S无关,因此有一定的鲁棒性
- 具有渐近收敛性,已在理论上被证明是一种以概率1收敛于全局最优解的全局优化算法
局部束搜索
记录k个状态而不是1个状态,从k个随机生成的状态开始,每一步生成所有k个状态的所有后继状态。如果有一个后继满足条件,则终止。否则,从整个后继列表中选择k个最佳的后继,重复这个过程。
遗传算法
局部束搜索的变形,通过将两个亲本结合后生成后继。从k个随机生成的状态(种群)开始,每个状态称之为个体。

具体案例实现《基于遗传算法的排课设计》
https://blog.csdn.net/weixin_42062229/article/details/94504604
对比
遗传算法:
优点是能很好的处理约束,能很好的跳出局部最优,最终得到全局最优解,全局搜索能力强;
缺点是收敛较慢,局部搜索能力较弱,运行时间长,且容易受参数的影响。
模拟退火:
优点是局部搜索能力强,运行时间较短;
缺点是全局搜索能力差,容易受参数的影响。
爬山算法:
显然爬山算法较简单,效率高,但是处理多约束大规模问题时力不从心,往往不能得到较好的解。
推荐案例实现:《优化搜索算法:爬山法,模拟退火算法,遗传算法-Python实现》
https://blog.csdn.net/bcj296050240/article/details/50839806
4.2连续空间的局部搜索
4.3 使用不确定动作的搜索
环境不确定,信息由感知提供。Agent的未来行动依赖于未来感知信息。问题的解是应急规划而不是一个序列。
4.4 使用部分可观察信息的搜索
第5章 对抗搜索
5.1博弈
对抗搜索:竞争环境中每个Agent的目标之间是有冲突的,也成为博弈。
博弈:有完整信息的、确定性的、轮流行动的、两个游戏者的零和游戏。
剪枝:在搜索树中忽略那些不影响最后决定的部分。
启发式评估函数:在不进行完全搜索的情况下估计某些状态的真实效用值。
博弈问题的形式化
S0: 初始状态,规范游戏开始的情况
Player(s):定义此时该谁行动
Actions(s):返回状态s下的合法动作集合
Result(s,a):转移模型,定义行动的结果
Terminal-Test(s): 终止测试 ,游戏的结束条件
Utility(s,p): 效用函数,定义游戏者p在终止状态s下的数值
5.2博弈中的优化决策
最优解:到达目标状态的一系列行动
中止状态:一方取胜
极小极大值:可以理解为有两个人MAX和MIN,MAX喜欢移动到有极大值的地方,MIN喜欢移动到有极小值的地方,终端状态由效用函数进行评价。MAX指向有最高极小极大值的中止状态。假设对手的决策均为最优。
5.2.1极小极大算法
递归算法自上而下一直前进到树的叶子节点,递归回溯通过搜索树把极小极大值回传。
每一步都是最小化敌方的最大收益。
5.2.2多人博弈时的最优决策
超过两个人的博弈利用MINIMAX算法,由于之前研究的两人博弈一方得分可以反应另一方得分,故仅用一个数值表示状态得分,对于多人游戏,应该使用向量值替换单一效用值。每个节点的回传至是该选手在节点的后继者效用值向量中选择的结果。多人博弈通常会涉及在游戏选手之间出现正式或非正式联盟的情况。
5.3α-β剪枝
极大极小值搜索时间复杂度呈指数级增加,α-β剪枝可以将复杂度减半,很多情况下可以剪裁掉整个子树。在某节点的父节点有更好的选择,则不会探索到该节点。
α:到目前为止路径上发现的MAX的最佳选择
β:到目前为止路径上MIN的最佳选择
比α小则停止探索,比β大则停止探索
int AlphaBeta(nPlay,nAlpha,nBeta)
{
if(game over)
return Eveluation; //胜负已分,返回估值
if(nPly==0)
return Eveluation; //叶子节点返回估值
if(Is Min Node) //判断 节点类型
{ // 极小值节点
for(each possible move m)
{
make move m; //生成新节点
score=AlphaBeta(nPly-1,nAlpha,nBeta)//递归搜索子节点
unmake move m;//撤销搜索过的节点
if(score=nBeta)
return nAlpha;//alpha剪枝,抛弃后继节点
}
}
return nBeta;//返回最小值
}
else
{//取极大值的节点
for(each possible move m)
{
make move m; //生成新节点
score=AlphaBeta(nPly-1,nAlpha,nBeta)//递归搜索子节点
unmake move m;//撤销搜索过的节点
if(score>nAlpha)
{
nAlpha=score;//取极小值
if(nAlpha>=nBeta)
return nBeta;//nBeta剪枝,抛弃后继节点
}
}
return nAlpha;//返回最小值
}
}
5.3.1行棋排序
α-β剪枝的效率很大程度上依赖于检查后继的顺序,对于随机顺序而言可以降低复杂度,引入一些简单的排序函数可以更大程度降低复杂度。存储以前见过的棋局的哈希表称为换位表。
5.4不完美的实时决策
由于实时决策允许的模拟时间很短,故需要尽早截断搜索、将启发式评估函数用于搜索。启发式评估函数EVAL(可以评估中间状态)–替代效用函数用省么时候调用EVAL的阶段测试–替代终止测试
5.4.1评估函数
①对终止状态的排序应该和真正的效用函数的排序结果一样②评估函数的计算成本不能花费太长时间③对于非终止状态,评估函数应该和取胜几率密切相关
5.4.2截断搜索
最简单的节点搜索:设置固定的搜索深度地平线效应:当好棋出现在固定搜索深度之后时,无法探索到好棋
5.4.3向前剪枝
向前剪枝:在某节点上无需进一步考虑而直接剪枝一些节点柱搜索:只考虑最好的n步行棋,但无法保证最好的行棋不被剪枝掉
第六章 约束满足问题
约束满足问题:
环境:单agent、延续、静态、完全可观察
一种特殊的搜索问题
约束满足问题 vs. 经典搜索问题:
状态s:一组变量(彼此之间有约束)的部分或全部赋值{x1,x2,…,xn}
动作:给每个变量赋不同的值 assignment(xi,v)
状态转移:Result(s, assignment(xi, v))=s’, s’中xi=v, 其它变量赋值与s一致
目标:所有变量都被赋值,且满足约束
当对问题中变量的赋值满足所有约束时,该赋值是相容的
CSP问题的解是所有变量的相容的、完整的赋值
约束满足问题的特性
可交换性 : 对变量赋值的顺序不影响最终结果
约束传播:一个变量的赋值将改变其它变量的值域
约束满足问题的描述
需要描述状态、后继函数、目标测试
最重要的是描述约束
任何CSP都可以转变为只含二元约束的CSP
高阶约束变为二元约束:引进新变量表示变量对的值,引进约束如“X是Y中第一个元素”
改变变量值域消除一元约束
标准搜索过程:
状态为到目前为止的赋值
初始状态: 空赋值, { }
后继函数: 对一个未赋值的变量赋一个可能值
目标检测: 完整的满足所有约束的赋值
与经典搜索的不同之处
Idea 1: 一次只考虑一个变量
Idea 2: 扩展节点时,只考虑当前变量的合法赋值
考虑以上两点的深度优先搜索称为回溯搜索
约束满足问题如何求解
CSP的关键特性: 可交换性和约束传播
下一次选择哪个变量来赋值?
选择值域最小的约束变元
策略1:最小剩余值(Minimum remaining values,MRV)
试图缩小分支因子
策略2:度启发式
选择最受约束的变量先赋值
减少后续变量的分支
在变量的值域中尝试的顺序是什么?
最少约束值(Least constraining value)
选择当前变量的所有可能值中对未赋值变量的值域约束最小的值
我们能否早些检测到失败?
向前检测
跟踪未赋值变量值域变化
当某个变量值域为空时,算法结束
弧相容
X —> Y 是相容的 当且仅当 x的每一个取值y都有可选的值
可以在每次赋值之前做一次弧相容检测
弧相容能够比前向检查更早地检测到失败
第七章 逻辑Agents
7.2 逻辑
逻辑是陈述式语言:
利用声明的语句推断问题空间中其它语句所代表的事件的真假
声明的语句代表问题空间中能够成立的事实
语法定义语句的形式,合法语句的规范
语义定义语句的意义,及语句在可能世界中的真值
模型
当对语句s中所有变量的赋值使得语句s的真值为true时,这个赋值被称为语句s的模型
知识库是语句的集合,记为KB
m是知识库的模型 当且仅当 m是知识库中所有语句的模型
一个知识库/语句是可满足的 当且仅当 它有至少一个模型。
一个知识库/语句是永假的 当且仅当 它没有模型。
一个知识库/语句是永真的 当且仅当 它对可能世界都为真
KB1 = {x+y=2, x-y=2} 是可满足的
KB2 = {x+y=2, x-y=1, xϵN, y ϵN} 是永假的
KB3 = {1>0} 是可满足的
知识库 KB 逻辑蕴含语句 a当且仅当 当KB 为真时,a总是为真:
KB ╞ a
x+y = 4 蕴含 4 = x+y
逻辑蕴含是语句之间的语义关系
通过蕴含关系,我们可以知道,除了知识库中已知的事实,还有哪些事实为真
7.3 命题逻辑:一种简单的逻辑
7.4 命题逻辑定理证明
模型检验:真值枚举
推理规则:
- 利用推理规则
- 归结定理
- 反证法:( KB ∧¬ α )永假