贝叶斯理论与函数拟合，最大似然与损失函数

最初的疑惑

在李航老师的统计机器学习当中，提到了机器学习的目标或者说求解的方向，这个目标分为两种形式：

• 机器学习是要去学习一个目标函数$f$或者说一个假设$h$，这个函数$f$或者假设$h$可以正确分类数据或者正确拟合数据
• 机器学习是要去学习一个概率分布$P(h|D)$，这个概率表达式的含义是在给定数据集$D$上，假设$h$是正确的概率是什么多少，我们只需要选取正确率最高的假设就可以，也就是求$maxP(h|D)$，得到假设$h$。

所以为什么机器学习模型的目标会有两种表达形式，这两种形式又有什么联系呢？

目标函数$f$与符合概率$P(h|D)$最大的假设$h$的现实世界的含义是什么？

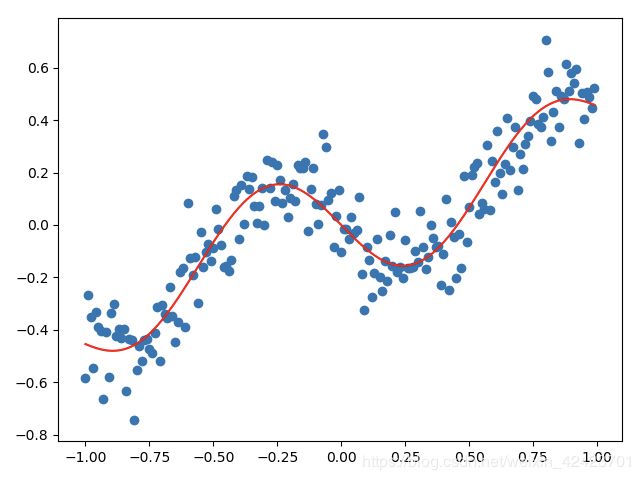
对于回归问题来说，两种表述现实世界的含义都可以通过下面的图片表示，这个目标函数$f$和假设$h$都表示为一个拟合曲线。在这里假设$h$可以理解为在某个模型中，所有参数$\theta$的取值，所以把$h$放入的模型当中，就能生成一个函数，一条曲线。

现在，我们先给前面提到的两个目标换一下名字，来表达更一般的问题

• 目标是拟合一个函数，那么我们就称它为函数拟合的方式，求解拟合问题，一般是通过损失函数的方式
• 目标如果是学习一个概率分布，找到最可能的假设，我们把它叫做贝叶斯的方式，求解贝叶斯，一般是通过“最大似然”的方式。

这样，我们的问题就变成了一个更加一般的问题，贝叶斯和函数拟合是什么关系？

贝叶斯和函数拟合是如何关联的？

首先给出结论：

贝叶斯的优化目标–最大似然 和函数拟合的优化目标–最小损失 在回归和分类问题上表达式完全一致的，并且优化风向也是一致的。

这里的联系虽然加了限制条件：回归和分类问题，但是这个限制其实是十分宽松的，因为回归和分类问题已经涵盖所有监督式机器学习，所以这个结论其实是一个一般性的结论。

同时，这里还要注意一点，$P(h|D)$为后验分布，但是如果我们假设先验分布$P(h)$，也就是每个假设$h$出现的概率是相同的，我们可以得到$P(h|D)\propto P(D|h)$，这个$P(D|h)$就是似然(likelihood)。所以找最大的$P(h|D)$的问题就变成了

最大似然和损失函数在回归问题上是如何关联的？

首先我们先回顾一下回归问题的基本形式：

我们希望找到一个 $W$ ，且有函数$f$
$$f(x)=\sum _{i=1}^n{w}_i\ast \varphi (x_i)+w_0$$
使预测的$f(x)$能够最够靠近真实值$y$。

如果用函数拟合的方式，我们会把损失函数定义为$MSE$，我们需要做的就是求解

$$ar{g}_{w}min\sum _{i=0}^n(y_i-f(x_i){)}^2$$

下面我们要用最大似然表示这个问题，并说明最大似然的形式和损失函数的形式是完全一致的。

我们首先假设真实的$y$和$f(x)$的关系为
$$y_i=f(x_i)+\epsilon$$
$\epsilon$是预测和真实之间的误差，或者噪音。这个公式表示每个训练样例的值是收到一个噪音干扰的，我们假设这个噪音是从均值为0，方差为$\sigma$的高斯分布中采样出来的，且当前$f(x_i)$的假设为$h$。所以我们可以得到
$$P(y_i-f(x_i)|h)=Normal(0,\sigma )$$
或者我们可以把形式转换一下，把y当做符合均值为$f(x_i)$，方差为$\sigma$的正太分布，所有我们又可以得到
$$P(y_i|h)=Normal(f(x_i),\sigma )$$
当我们知道了$P(y_i|h)$的形式之后，我们可以用最大似然来表示这个问题了
$$h_{ML}=arg\underset{h\in H}{\max }P(Y|h)$$
因为$P(y_i|h)$是从$\epsilon$的独立同分布的高斯分布这个假设得来的，所以$P(y_i|h)$同样是独立同分布的，所以$h_{ML}$可以写成$P(y_i|h)$乘积的形式，得到
$$h_{ML}=arg\underset{h\in H}{\max }\prod _{i=1}^{n}P(y_i|h)$$
根据$P(y_i|h)$是高斯分布，我们可以得到下面的表达式:
$$h_{ML}=arg\underset{h\in H}{\max }\prod _{i=0}^n\frac{1}{\sqrt{2\pi {\sigma }^2}}exp(\frac{(y_i-f(x_i){)}^2}{-2{\sigma }^2})$$
我们转化这个表达式为做$log$运算，之所以可以这么做，是因为log可以转化乘的形式为加的形式，且log函数是单调的，不会改变优化方向
$$h_{ML}=arg\underset{h\in H}{\max }\sum _{i=0}^{n}log\frac{1}{\sqrt{2\pi {\sigma }^2}}-\frac{(y_i-f(x_i){)}^2}{2{\sigma }^2}$$
以为$log\frac{1}{\sqrt{2\pi {\sigma }^2}}$与$h$无关，所以可以忽略
$$h_{ML}=arg\underset{h\in H}{\max }\sum _{i=0}^n-\frac{(y_i-f(x_i){)}^2}{2{\sigma }^2}$$
去掉右边的负号，我们可以把求最大值变为求最小值
$$h_{ML}=arg\underset{h\in H}{\min }\sum _{i=0}^n\frac{(y_i-f(x_i){)}^2}{2{\sigma }^2}$$
再次掉与$h$无关的常数$\sigma$，可以得到
$$h_{ML}=arg\underset{h\in H}{\min }\sum _{i=0}^n(y_i-f(x_i){)}^2$$

到此证明结束，很容易看到最大似然和损失函数的表达方式是完全一致的。

最大似然和损失函数在分类问题上是如何关联的？

对于分类问题来说，常用的损失函数–交叉熵本身就是从概率角度推导出来的。当然，通过函数拟合去学习一个曲线或者一个平面去分割数据同样也是可行的，支持向量机–SVM就是这种方法比较常见的表现方式。不过在这里，我们主要讨论损失函数的从概率方向的解释。

我们假设有一个二分类问题，数据集$D$是线性可分得，且数据集分为$X,Y$俩部分，$X$为模型的输入，$Y$为模型的输出，$Y$的取值是0或1，根绝最大似然的思路，我们希望找到似然$P(Y|h,X)$的最大概率，$h$是我们模型遵循的假设，也可以理解为模型本身。

因为上面的方程是对于所有输入$X$来说的，其实就是一个联合概率分布，又因为$x_i$之间相互独立，所以可以变为累乘的形式
$$P(Y|H,X)=\prod _{i=1}^{n}P(y_i|h,x_i)$$
对每一个数据对$x_i,y_i$，在某一个模型假设($h$)下，分类为0的概率$P(y_i=1|h,x_i)=h(x_i)$，分类为1的概率$P(y_i=0|h,x_i)=1-h(x_i)$。

很显然这个概率是个伯努利分布，所以我们的似然(Likelihood)就可以表示为:
$$P(y_i|h,x_i)=h(x_i{)}^{y_i}(1-h(x_i){)}^{1-y_i}$$
带入到上面的累乘的公式我们可以得到：
$$P(Y|h,x_1,x_2,...x_n)=\prod _{i=1}^{n}P(y_i|h,x_i)=\prod _{i=1}^{n}h(x_i{)}^{y_i}(1-h(x_i){)}^{1-y_i}$$
因为我们要求其最大似然，我们用$h_{ML}$表示，也就是
$$h_{ML}=arg\underset{h\in H}{\max }\prod _{i=1}^{n}h(x_i{)}^{y_i}(1-h(x_i){)}^{1-y_i}$$
对后面的累乘形式求$\log$，我们可以得到
$$h_{ML}=arg\underset{h\in H}{\max }\sum _{i=1}^n(y_i\ast \log (h(x_i))+(1-y_i)\ast \log (1-h(x_i)))$$
最后把求最大值，变为求最小的值，就变成了分类的损失函数
$$loss=arg\underset{h\in H}{\min }\sum _{i=1}^n-(y_i\ast \log (h(x_i))+(1-y_i)\ast \log (1-h(x_i)))$$

如何通过最大似然优化神经网络？

这个问题本身可能就是一个伪问题，因为从上面的讨论我们就可以得出，在很多问题上神经网络都是在通过最小化负的似然函数–也就是最大化似然函数来求解。所以本质上来说用损失函数+反向传播算法，就是在用最大似然优化神经网络了。

为什么人们更喜欢贝叶斯的表达方式？

因为贝叶斯的可解释性更强，但其实人们并没有偏爱这两种理解问题的方式中的某一种。其实从概率角度去理解机器学习和从非概率的角度去理解机器学习，这两种方式都是很有效的解决问题的方式，比如说对于深度学习这种类型的机器学习算法来说，其实是非概率的角度先行的，虽然缺少了一些可解释性，但是确实很有效，所以在机器学习领域应该培养从不同角度去思考问题的习惯。同时又因为机器学习本身就是交叉学科，和计算机，数学，物理，统计，甚至神经科学都密不可分，所以更应该更加灵活地去理解和解决问题。

AlphaGo Zero的损失函数的贝叶斯解释

虽然AlphaGo Zero整体的架构是属于增强学习的，不过在训练神经网络的时候其实是监督学习，其损失函数如下：

$$loss=(z-v{)}^2-{\pi }^{T}log(P)+\lambda ||\theta |{|}^2$$
v是对某一个状态值的预测，z是这个状态的真实值，$\pi$是选择的动作的值，$P$是选择这个动作的概率，最后的$\lambda ||\theta |{|}^2$为正则项，为了防止过拟合的。

其实不难发现，这个损失函数是回归和分类损失函数的加和，但是我们知道“求和”在log函数里面表示为相乘，所以可以把这个函数理解为在最大化一个分类和回归问题的联合概率分布，也就是

$$P(v,action={\pi }_i|vz\pi )=P(v|z)\ast P(action={\pi }_i|\pi )$$

$P(v|z)$是回归问题，希望根据真实的状态值$z$给出最可能的估计值$v$(最大似然估计)， $P(action={\pi }_i|\pi )$是分类问题，希望根据每一个动作的概率，估算出一个概率最大的行为。 因为这两个分布是相互独立的，所以可以相乘，然后取负，再取$log$，就得到了AlphaGo Zero的损失函数，所以本质上AlphaGo Zero的损失函数也是最大似然估计。