深蓝学院从零开始手写VIO（三）——滑动窗口理论

声明：本专栏文章为深蓝学院《从零开始手写VIO》课程个人学习笔记，更多学习资源请咨询深蓝学院相关课程。

SLAM问题的概率建模

最大后验估计与加权最小二乘

SLAM问题可以建模为一个贝叶斯估计问题（关于贝叶斯估计的相关内容可参见另一篇文章——贝叶斯滤波）。对于SLAM问题来说，记待估计变量为$\mathcal{X}=\{{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_m\}$，观测量为$\mathcal{Z}=\{{\mathbf{z}}_1,{\mathbf{z}}_2,\cdots ,{\mathbf{z}}_n\}$，那么根据贝叶斯法则有：
$$p(\mathcal{X}|\mathcal{Z})=\frac{p(\mathcal{Z}|\mathcal{X})p(\mathcal{X})}{p(\mathcal{Z})}$$

式中称为先验概率，称为似然概率，称为后验概率。SLAM状态估计的本质就是寻找到一个状态变量${\mathcal{X}}^{\ast }$使得后验概率最大，即求解最大后验（maximum a posterior，MAP）的过程：
$$\begin{array}{rl}{\mathcal{X}}^{\ast }& =\arg \underset{\mathcal{X}}{\max }(p(\mathcal{X}|\mathcal{Z}))\\ & =\arg \underset{\mathcal{X}}{\max }\frac{p(\mathcal{Z}|\mathcal{X})p(\mathcal{X})}{p(\mathcal{Z})}\end{array}$$

略去与$\mathcal{X}$无关的$p(\mathcal{Z})$并将上式展开有：
$${\mathcal{X}}^{\ast }=\arg \underset{\mathcal{X}}{\max }\prod _{i=1}^{n}p({\mathbf{z}}_i|\mathcal{X})p(\mathcal{X})$$

上式的求解需要明确式中各概率分布的具体形式，与贝叶斯滤波类似我们同样先来看符合高斯分布的情况。在高斯分布下，对上式求解$-\log$将求解最大值（$\arg \max$）转变为求解最小值（$\arg \min$）有：
$${\mathcal{X}}^{\ast }=\arg \underset{\mathcal{X}}{\min }\sum _{i=1}^n-\log (p({\mathbf{z}}_i|\mathcal{X}))-log(p(\mathcal{X}))$$

假设$p({\mathbf{z}}_i|\mathcal{X})\sim N({\mathbf{\mu }}_i,{\mathbf{\Sigma }}_i)$，$p(\mathcal{X})\sim N({\mathbf{\mu }}_{\mathcal{X}},{\mathbf{\Sigma }}_{\mathcal{X}})$，将其概率分布带入上式有：
$${\mathcal{X}}^{\ast }=\arg \underset{\mathcal{X}}{\min }\sum _{i=1}^n({\mathbf{z}}_i-{\mathbf{\mu }}_i{)}^T{\mathbf{\Sigma }}_i^{-1}({\mathbf{z}}_i-{\mathbf{\mu }}_i)+(\mathcal{X}-{\mathbf{\mu }}_{\mathcal{X}}{)}^T{\mathbf{\Sigma }}_{\mathcal{X}}^{-1}(\mathcal{X}-{\mathbf{\mu }}_{\mathcal{X}})$$

可以看到，在高斯分布下，求解MAP问题就等价于求解一个加权最小二乘问题，这里的加权矩阵是协方差矩阵的逆${\mathbf{\Sigma }}^{-1}$，由于其表征了不同误差权重的信息量，因此其也称为信息矩阵$\mathbf{\Lambda }={\mathbf{\Sigma }}^{-1}$。

一个简单的例子

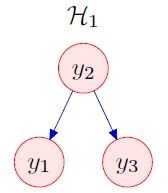
对于上图所示的贝叶斯网络（原图及更多例子参见文献：Preamble to ‘The Humble Gaussian Distribution’. David MacKay），假设各变量之间的关系（这里出于习惯问题，使用$x$代替图中的$y$）如下：
$$\{\begin{array}{rl}{x}_2& =v_2,v_2\sim N(0,{\sigma }_2^2)\\ x_1& =w_1{x}_2+v_1,v_1\sim N(0,{\sigma }_1^2)\\ x_3& =w_3{x}_2+v_3,v_3\sim N(0,{\sigma }_3^2)\end{array}$$

这里由于三个变量均值均为0，因此其协方差矩阵为（式中$\mathbf{x}=[x_1,x_2,x_3{]}^T$）：
$$\begin{array}{rl}\mathbf{\Sigma }& =E(\mathbf{x}{\mathbf{x}}^T)-E(\mathbf{x}{)}^2=E(\mathbf{x}{\mathbf{x}}^T)\\ & =E\left(\left[\begin{array}{ccc}{x}_1{x}_1& x_1{x}_2& x_1{x}_3\\ x_2{x}_1& x_2{x}_2& x_2{x}_3\\ x_3{x}_1& x_3{x}_2& x_3{x}_3\end{array}\right]\right)\\ & =\left[\begin{array}{ccc}E(x_1{x}_1)& E(x_1{x}_2)& E(x_1{x}_3)\\ E(x_2{x}_1)& E(x_2{x}_2)& E(x_2{x}_3)\\ E(x_3{x}_1)& E(x_3{x}_2)& E(x_3{x}_3)\end{array}\right]\end{array}$$

协方差矩阵中的各元素都可以通过对应的变换求出，这里给个例子，其余项可以按照同样方法计算：
$$\begin{array}{rl}E(x_1{x}_3)& =E((w_1{x}_2+v1)(w_3{x}_2+v_3))\\ & =E(w_1{w}_3{x}_2^2+w_1{x}_2{v}_3+w_3{v}_1{x}_2+v_1{v}_3)\\ & =w_1{w}_{3}E(x_2^2)=x_1{x}_3{\sigma }_2^2\end{array}$$

最终的协方差矩阵为：
$$\mathbf{\Sigma }=\left[\begin{array}{ccc}{w}_1^2{\sigma }_2^2+{\sigma }_1^2& w_1{\sigma }_2^2& w_1{w}_3{\sigma }_2^2\\ w_1{\sigma }_2^2& {\sigma }_2^2& w_3{\sigma }_2^2\\ w_1{w}_3{\sigma }_2^2+{\sigma }_1^2& w_3{\sigma }_2^2& w_3{\sigma }_2^2+{\sigma }_3^2\end{array}\right]$$

在获取了协方差矩阵$\mathbf{\Sigma }$后，如果我们直接通过求逆的方式求解信息矩阵$\mathbf{\Lambda }$无疑是较为复杂的。另一方面，在高斯分布的概率密度函数的指数项中，天然存在着信息矩阵和变量的乘积形式${\mathbf{x}}^T\mathbf{\Lambda }\mathbf{x}$，因此如果我们能求解出$\mathbf{x}$的概率密度函数即可从中分解出信息矩阵$\mathbf{\Sigma }$。

对于本例，根据其对应的贝叶斯网络模型有：
$$\begin{array}{rl}p(x_1,x_2,x_3)& =p(x_2)p(x_1|x_2)p(x_3|x_2)\\ & =\frac{1}{Z_2}\exp (-\frac{x_2^2}{2{\sigma }_2^2})\frac{1}{Z_1}\exp (-\frac{(x_1-w_1{x}_2{)}^2}{2{\sigma }_1^2})\frac{1}{Z_3}\exp (-\frac{(x_3-w_3{x}_2{)}^2}{2{\sigma }_2^2})\\ & =\frac{1}{Z_2{Z}_1{Z}_3}\exp \left(-\frac{x_2^2}{2{\sigma }_2^2}-\frac{(x_1-w_1{x}_2{)}^2}{2{\sigma }_1^2}-\frac{(x_3-w_3{x}_2{)}^2}{2{\sigma }_2^2}\right)\\ & =\frac{1}{Z_2{Z}_1{Z}_3}\exp \left(-x_2^2\left[\frac{1}{2{\sigma }_2^2}+\frac{w_1^2}{2{\sigma }_1^2}+\frac{w_3^2}{2{\sigma }_3^2}\right]-x_1^2\frac{1}{2{\sigma }_1^2}+2x_1{x}_2\frac{w_1}{2{\sigma }_1^2}-x_3^2\frac{1}{2{\sigma }_3^2}+2x_2{x}_3\frac{w_3}{2{\sigma }_3^2}\right)\\ & =\frac{1}{Z_2{Z}_1{Z}_3}\exp \left(-\frac{1}{2}\left[\begin{array}{ccc}{x}_1& x_2& x_3\end{array}\right]\left[\begin{array}{ccc}\frac{1}{{\sigma }_1^2}& -\frac{w_1}{{\sigma }_1^2}& 0\\ -\frac{w_1}{{\sigma }_1^2}& \left[\frac{1}{{\sigma }_2^2}+\frac{w_1^2}{{\sigma }_1^2}+\frac{w_3^2}{{\sigma }_3^2}\right]& -\frac{w_3}{{\sigma }_3^2}\\ 0& -\frac{w_3}{{\sigma }_3^2}& \frac{1}{{\sigma }_3^2}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]\right)\end{array}$$

注意这里虽然$x_1,x_2,x_3$各自的边缘分布都是零均值的，但条件分布并不是。这里给出信息矩阵的几条性质：

• 信息矩阵中的0项表示对应变量在给定其他标量的条件下，互相独立；
• 信息矩阵中的系数大于零，则两个变量之间负相关；系数小于零，则两个变量之间正相关；

在本例的信息矩阵中，${\Lambda }_{13}={\Lambda }_{31}=0$，这意味着变量$x_1$和$x_3$在给定条件$x_2$的条件下是互相独立的，而初始的协方差矩阵二者的对象项并不为零，表示两者的边缘分布并不是独立的。

舒尔补、条件概率与边缘概率

在高斯分布下，由联合分布求解条件分布中的协方差传递过程，本质上是求解分块矩阵舒尔补的过程（具体参见滤波估计理论（二）——卡尔曼滤波）。但在求解加权最小二乘问题中，我们需要进行操作的往往是信息矩阵而非协方差矩阵，在进一步讨论钱，这里我们首先引入一个重要的定理。

定理1：舒尔补求逆定理。对于分块矩阵$\mathbf{M}=\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ \mathbf{C}& \mathbf{D}\end{array}\right]$，其可以化为如下的形式，其中${\Delta }_{\mathbf{A}}$为矩阵$\mathbf{A}$相对于矩阵$\mathbf{M}$的舒尔补：
$$\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ \mathbf{C}& \mathbf{D}\end{array}\right]=\left[\begin{array}{cc}\mathbf{I}& 0\\ \mathbf{C}{\mathbf{A}}^{-1}& \mathbf{I}\end{array}\right]\left[\begin{array}{cc}\mathbf{A}& 0\\ 0& {\Delta }_{\mathbf{A}}\end{array}\right]\left[\begin{array}{cc}\mathbf{I}& {\mathbf{A}}^{-1}\mathbf{B}\\ 0& \mathbf{I}\end{array}\right]$$

那么矩阵$\mathbf{M}$的逆可以写为：
$${\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ \mathbf{C}& \mathbf{D}\end{array}\right]}^{-1}=\left[\begin{array}{cc}\mathbf{I}& -{\mathbf{A}}^{-1}\mathbf{B}\\ 0& \mathbf{I}\end{array}\right]\left[\begin{array}{cc}\mathbf{A}& 0\\ 0& {\Delta }_{\mathbf{A}}\end{array}\right]\left[\begin{array}{cc}\mathbf{I}& 0\\ -\mathbf{C}{\mathbf{A}}^{-1}& \mathbf{I}\end{array}\right]$$

在了解这一定理之后，我们来看一个简单的例子。假设存在多元高斯分布$\mathbf{x}=[a,b],a\sim N(0,A),b\sim N(0,B)$，则$\mathbf{x}$的协方差矩阵和对应的信息矩阵为：
$$\begin{array}{rl}\mathbf{\Sigma }& =\left[\begin{array}{cc}\mathbf{A}& {\mathbf{C}}^T\\ \mathbf{C}& \mathbf{B}\end{array}\right]\\ \mathbf{\Lambda }={\mathbf{\Sigma }}^{-1}& =\left[\begin{array}{cc}\mathbf{I}& -{\mathbf{A}}^{-1}{\mathbf{C}}^T\\ 0& \mathbf{I}\end{array}\right]\left[\begin{array}{cc}{\mathbf{A}}^{-1}& 0\\ 0& {\Delta }_{\mathbf{A}}^{-1}\end{array}\right]\left[\begin{array}{cc}\mathbf{I}& 0\\ -\mathbf{C}{\mathbf{A}}^{-1}& \mathbf{I}\end{array}\right]\\ & =\left[\begin{array}{cc}\mathbf{I}& -{\mathbf{A}}^{-1}{\mathbf{C}}^T\\ 0& \mathbf{I}\end{array}\right]\left[\begin{array}{cc}{\mathbf{A}}^{-1}& 0\\ -{\Delta }_{\mathbf{A}}^{-1}\mathbf{C}{\mathbf{A}}^{-1}& \Delta {\mathbf{A}}^{-1}\end{array}\right]\\ & =\left[\begin{array}{cc}{\mathbf{A}}^{-1}+{\mathbf{A}}^{-1}{\mathbf{C}}^T{\Delta }_{\mathbf{A}}^{-1}\mathbf{C}{\mathbf{A}}^{-1}& -{\mathbf{A}}^{-1}{\mathbf{C}}^T{\Delta }_{\mathbf{A}}^{-1}\\ -{\Delta }_{\mathbf{A}}^{-1}\mathbf{C}{\mathbf{A}}^{-1}& {\Delta }_{\mathbf{A}}^{-1}\end{array}\right]\\ & =\left[\begin{array}{cc}{\Lambda }_{11}& {\Lambda }_{12}\\ {\Lambda }_{21}& {\Lambda }_{22}\end{array}\right]\end{array}$$

从联合分布的信息矩阵中，我们可以分解出边缘分布的信息矩阵为：
$$\begin{array}{rl}{\mathbf{\Lambda }}_A={\mathbf{A}}^{-1}& =({\mathbf{A}}^{-1}+{\mathbf{A}}^{-1}{\mathbf{C}}^T{\Delta }_{\mathbf{A}}^{-1}\mathbf{C}{\mathbf{A}}^{-1})-({\mathbf{A}}^{-1}{\mathbf{C}}^T{\Delta }_{\mathbf{A}}^{-1})({\Delta }_{\mathbf{A}})({\Delta }_{\mathbf{A}}^{-1}\mathbf{C}{\mathbf{A}}^{-1})\\ & ={\Lambda }_{11}-{\Lambda }_{12}{\Lambda }_{22}^{-1}{\Lambda }_{21}\end{array}$$

即我们从概率分布$p(a,b)$中获得了边缘化变量$b$后的边缘概率$p(a)$对应的信息矩阵。

滑动窗口算法

对于加权最小二乘问题，其具有如下形式的正则方程：
$${\mathbf{J}}^T{\mathbf{\Sigma }}^{-1}\mathbf{J}\delta \mathcal{X}=-{\mathbf{J}}^T{\mathbf{\Sigma }}^{-1}\mathbf{r}$$

为了方便，我们通常也会记$\mathbf{\Lambda }={\mathbf{J}}^T{\mathbf{\Sigma }}^{-1}\mathbf{J}$，也称其为信息矩阵。
在滑窗算法中，每当新的状态量进入窗口时，由于窗口的尺寸是一定的，我们需要去除旧的状态量并添加新的状态量。那么我们能否直接抛弃旧的状态量呢？答案是并不可以，例如在上图所示的模型中，在新的状态量$x_7$来临时，我们如果直接删除最老的状态量$x_1$，那么变量$x_2-x_5$将相互独立，这将破坏状态量之间的约束关系。从概率的角度来看，滑动窗口可以视为一个联合概率密度函数$p(x_1,x_2,x_3,x_4,x_5,x_6)$移除老状态量的过程，就相当于我们需要从该联合概率密度函数中求解边缘分布$p(x_2,x_3,x_4,x_5,x_6)$，而在大多数情况下，$p(x_1,x_2,x_3,x_4,x_5,x_6)\ne p(x_2,x_3,x_4,x_5,x_6)p(x_1)$，因此我们需要采用另一种策略去处理旧变量，获得边缘分布，即旧变量的边缘化（marginalization）过程（上图中c所示）。

可以看出，边缘化之后，剩余的变量之间并非完全独立的，而是依旧存在依赖关系。而我们知道，信息矩阵中的非零项表征了各状态量之间的条件独立性，下图给出了从联合分布的信息矩阵中边缘化掉（边缘化过程参见上面的舒尔补求逆定理）$x_1$过程中信息矩阵的变化过程。如果我们从信息矩阵$\mathbf{\Lambda }$中直接去掉$x_1$，得到的信息矩阵为${\mathbf{\Lambda }}_{aa}$；而边缘化$x_1$之后得到的信息矩阵为${\Lambda }_{aa}-{\Lambda }_{ab}{\Lambda }_{bb}^{-1}{\Lambda }_{ba}$，相比于${\mathbf{\Lambda }}_{aa}$，其填充了（fill-in）了许多的非零项，这与上图中的边正是一一对应的。

FEJ算法

记需要边缘化的变量为${\mathbf{x}}_m$，剩余变量为${\mathbf{x}}_r$，对应的的marginalization过程为：
$$\begin{array}{rl}\left[\begin{array}{cc}{\mathbf{\Lambda }}_{mm}& {\mathbf{\Lambda }}_{mr}\\ {\mathbf{\Lambda }}_{rm}& {\mathbf{\Lambda }}_{rr}\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_m\\ {\mathbf{x}}_r\end{array}\right]& =-\left[\begin{array}{c}{\mathbf{b}}_{mm}\\ {\mathbf{b}}_{mr}\end{array}\right]\\ \left[\begin{array}{cc}{\mathbf{\Lambda }}_{mm}& {\mathbf{\Lambda }}_{mr}\\ 0& {\mathbf{\Lambda }}_{rr}-{\mathbf{\Lambda }}_{rm}{\mathbf{\Lambda }}_{mm}^{-1}{\mathbf{\Lambda }}_{mr}\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_m\\ {\mathbf{x}}_r\end{array}\right]& =-\left[\begin{array}{c}{\mathbf{b}}_{mm}\\ {\mathbf{b}}_{mr}-{\mathbf{\Lambda }}_{rm}{\mathbf{\Lambda }}_{mm}^{-1}{\mathbf{b}}_{mm}\end{array}\right]\end{array}$$

我们记${\mathbf{\Lambda }}_p={\mathbf{\Lambda }}_{rr}-{\mathbf{\Lambda }}_{rm}{\mathbf{\Lambda }}_{mm}^{-1}{\mathbf{\Lambda }}_{mr}$，${\mathbf{b}}_p={\mathbf{b}}_{mr}-{\mathbf{\Lambda }}_{rm}{\mathbf{\Lambda }}_{mm}^{-1}{\mathbf{b}}_{mm}$，称之为先验信息矩阵和先验残差。

在新的变量添加到窗口后，新构建最小二乘问题的信息矩阵和残差变为（下标a表示新添加变量）：
$$\begin{array}{rl}\mathbf{\Lambda }& ={\mathbf{\Lambda }}_p+{\mathbf{J}}_a^T{\mathbf{\Sigma }}_a^{-1}{\mathbf{J}}_a\\ \mathbf{b}& ={\mathbf{b}}_p+{\mathbf{J}}_a^T{\mathbf{\Sigma }}_a^{-1}\mathbf{r}\end{array}$$

为了更好的理解这一过程，我们继续看上面的例子。假设在从滑窗中删除了旧变量$x_1$后，接下来我们需要向滑窗中添加新的变量$x_7$，那么新的信息矩阵构成过程如下图所示。我们发现，在左上角$x_2$对应的子矩阵是由第$k$步求得的先验信息矩阵（蓝色）和第$k+1$步求得的信息矩阵（粉色）叠加而来的，而这个信息矩阵在求解的时候，其线性化点是不同的，而这会使得求解的零空间发生变化。
为解决这一问题，在进行滑窗算法时，我们需要使用First Estimated Jacobian（FEJ）算法，将两次求解Jacobian矩阵时的线性化点保持一致。