电路前四章复习
第一章 电路模型和电路定律
1-1 电路和电路模型
电阻元件:表示消耗电能的元件。
电感元件:表示产生磁场,储存磁场能量的元件。
电容元件:表示产生电场,储存电场能量的元件。
电压源和电流源:表示将其他形式的能量转变成电能的元件。
基本理想电路元件有三个特征:
(a)只有两个端子;
(b)可以用电压或电流按数学方式描述;
(c)不能被分解为其他元件。
1-2 电流和电压的参考方向
无
1-3 电功率和能量
电功率:单位时间内电场力所作的功。
p = d w d t u = d w d q i = d q d t p=\frac{d w}{d t}\ \ \ \ \ \ \ \ \ \ u=\frac{d w}{d q}\ \ \ \ \ \ \ \ \ \ i=\frac{d q}{d t} p=dtdw u=dqdw i=dtdq
p = u i p=ui p=ui
1-4 电路元件
如果表征元件端子特性的数学关系式是线性关系,该元件称为线性元件,否则称为非线性元件。
集总参数电路
由集总元件构成的电路
集总元件 --> 假定发生的电磁过程都集中在元件内部进行。
集总条件 --> l<<λ
注意:
集总参数电路中u、i 可以是时间的函数,但与空间坐标无关。因此
任何时刻,流入两端元件一个端子的电流等于从另一端子流出的电流;
端子间的电压为确定值。
1-5 电阻元件
对电流呈现阻力的元件。
线性时不变电阻元件: 任何时刻端电压与电流成正比的电阻元件。
u = R i R = u i i = u R = G u u=Ri\ \ \ \ \ \ \ \ \ \ R=\frac{u}{i}\ \ \ \ \ \ \ \ \ \ i=\frac{u}{R}=Gu u=Ri R=iu i=Ru=Gu
R为电阻,单位 Ω \Omega Ω(欧姆)
G为电导,单位 S S S(西门子)
欧 姆 定 律 = { 只 适 用 于 线 性 电 阻 ( R 为 常 数 ) 。 如 电 阻 上 的 电 压 与 电 流 参 考 方 向 非 关 联 , 公 式 中 应 冠 以 负 号 。 线 性 电 阻 是 无 记 忆 、 双 向 性 的 元 件 。 欧姆定律=\begin{cases} 只适用于线性电阻( R 为常数)。\\ 如电阻上的电压与电流参考方向非关联,公式中应冠以负号。\\ 线性电阻是无记忆、双向性的元件。 \end{cases} 欧姆定律=⎩⎪⎨⎪⎧只适用于线性电阻(R为常数)。如电阻上的电压与电流参考方向非关联,公式中应冠以负号。线性电阻是无记忆、双向性的元件。
1-6 电压源和电流源
理想电压源:其两端电压总能保持定值或一定的时间函数,其值与流过它的电流 i 无关的元件叫理想电压源。
电源两端电压由电源本身决定,与外电路无关;与流经它的电流方向、大小无关。
通过电压源的电流由电源及外电路共同决定。
理想电流源:其输出电流总能保持定值或一定的时间函数,其值与它的两端电压u 无关的元件叫理想电流源。
电流源的输出电流由电源本身决定,与外电路无关;与它两端电压的方向、大小无关。
电流源两端的电压由电源及外电路共同决定。
1-7 受控电源(非独立源)
电压或电流的大小和方向不是给定的时间函数,而是受电路中某处的电压(或电流)控制的电源,称为受控电源。
受控源与独立源的比较
独立源电压(或电流)由电源本身决定,与电路中其他电压、电流无关,而受控源电压(或电流)由控制量决定。
独立源在电路中起“激励”作用,在电路中产生电压、电流,而受控源是反映电路中某处的电压或电流对另一处的电压或电流的控制关系,
在电路中不能作为“激励”。
1-8 基尔霍夫定律
基尔霍夫电流定律 (KCL)
在集总参数电路中,任意时刻,对任意结点流出(或流入)该结点电流的代数和等于零。
基尔霍夫电压定律 (KVL)
在集总参数电路中,任一时刻,沿任一回路,所有支路电压的代数和恒等于零。
小结
KCL是对支路电流的线性约束,KVL是对支路电压的线性约束。
KCL、KVL与组成支路的元件性质及参数无关。
KCL表明在每一结点上电荷是守恒的;KVL是能量守恒的具体体现(电压与路径无关)。
KCL、KVL只适用于集总参数的电路。
第二章 电阻电路的等效变换
2-2 电路的等效变换
二端电路(网络)
任何一个复杂的电路, 向外引出两个端钮,且从一个端子流入的电流等于从另一个端子流出的电流,
则称这一电路为二端网络 (或一端口网络)。
电路等效变换的条件:两电路端口处具有相同的电压电流关系(Voltage Current Relationship)。
电路等效变换的对象:未改变的外电路A中的电压、电流和功率。(即对外等效,对内不等效)
电路等效变换的目的:化简电路,方便计算。
2-3 电阻的串联和并联
电阻串联
各电阻顺序连接,流过同一电流 (KCL)。
总电压等于各串联电阻的电压之和 (KVL)。
功率
电阻串联时,各电阻消耗的功率与电阻大小成正比。
等效电阻消耗的功率等于各串联电阻消耗功率的总和。
u = R 1 i + . . . + R k i + . . . + R n i = ( R 1 + . . . + R n ) i = R e q i u=R_1i+...+R_ki+...+R_ni=(R_1+...+Rn)i=R_{eq}i u=R1i+...+Rki+...+Rni=(R1+...+Rn)i=Reqi
两 电 阻 分 压 u 1 = R 1 R 1 + R 2 u u 2 = R 2 R 1 + R 2 u 两电阻分压\ \ \ \ \ u_1=\frac{R_1}{R_1+R_2}u\ \ \ \ \ u_2=\frac{R_2}{R_1+R_2}u 两电阻分压 u1=R1+R2R1u u2=R1+R2R2u
电阻并联
各电阻两端为同一电压(KVL)。
总电流等于流过各并联电阻的电流之和(KCL)。
功率
电阻并联时,各电阻消耗的功率与电阻大小成反比。
等效电阻消耗的功率等于各并联电阻消耗功率的总和。
等 效 电 阻 由 ( K C L ) 可 得 : i = i 1 + i 2 + . . . + i n = u R 1 + u R 2 + . . . + u R n = u G e q 等效电阻 \ \ \ 由(KCL)可得:i=i_1+i_2+...+i_n=\frac{u}{R_1}+\frac{u}{R_2}+...+\frac{u}{R_n}=uG_{eq} 等效电阻 由(KCL)可得:i=i1+i2+...+in=R1u+R2u+...+Rnu=uGeq
1 R e q = u R 1 + u R 2 + . . . + u R n \frac{1}{R_{eq}}=\frac{u}{R_1}+\frac{u}{R_2}+...+\frac{u}{R_n} Req1=R1u+R2u+...+Rnu
两 电 阻 分 流 i 1 = 1 R 1 1 R 1 + 1 R 2 i = R 2 R 1 + R 2 i 两电阻分流\ \ \ \ \ i_1=\frac{\frac{1}{R_1}}{\frac{1}{R_1}+\frac{1}{R_2}}i=\frac{R_2}{R_1+R_2}i 两电阻分流 i1=R11+R21R11i=R1+R2R2i
串、并联电路求解的一般步骤:
求出等效电阻或等效电导。
应用欧姆定律求出总电压或总电流。
应用欧姆定律或分压、分流公式求各电阻上的电流和电压。
2-4 电阻a的Y形联结和 Δ \Delta Δ形联结的等效变换
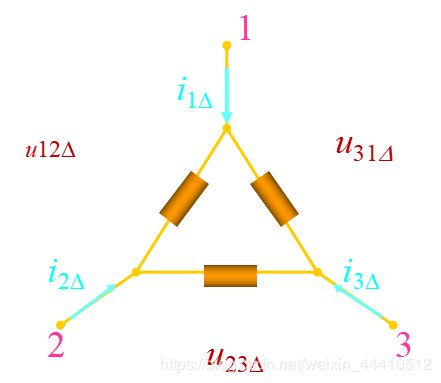
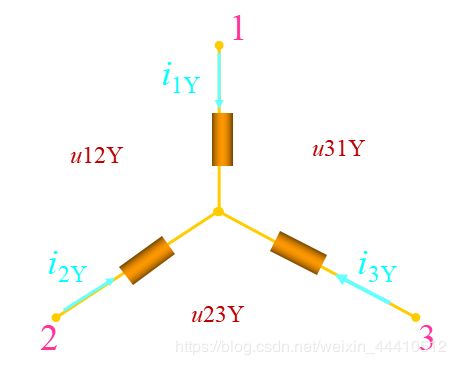
等效条件:
i 1 Δ = i 1 Y i 2 Δ = i 2 Y i 3 Δ = i 3 Y i_{1Δ} =i_{1Y} \ \ \ \ i_{2 Δ} =i_{2Y} \ \ \ \ i_{3 Δ} =i_{3Y} i1Δ=i1Y i2Δ=i2Y i3Δ=i3Y
u 12 Δ = u 12 Y u 23 Δ = u 23 Y u 31 Δ = u 31 Y u_{12Δ} =u_{12Y} \ \ \ \ u_{23 Δ} =u_{23Y} \ \ \ \ u_{31 Δ} =u_{31Y} u12Δ=u12Y u23Δ=u23Y u31Δ=u31Y
Δ 形 联 结 : 用 电 压 表 示 电 流 { i 1 Δ = u 12 Δ R 12 − u 31 Δ R 31 i 2 Δ = u 23 Δ R 23 − u 12 Δ R 12 i 3 Δ = u 31 Δ R 31 − u 23 Δ R 23 Δ形联结:用电压表示电流\begin{cases} i_{1 Δ}=\frac{u_{12 Δ}}{R_{12}}-\frac{u_{31 Δ}}{R_{31}}\\ i_{2 Δ}=\frac{u_{23 Δ}}{R_{23}}-\frac{u_{12 Δ}}{R_{12}}\\ i_{3 Δ}=\frac{u_{31 Δ}}{R_{31}}-\frac{u_{23 Δ}}{R_{23}} \end{cases} Δ形联结:用电压表示电流⎩⎪⎨⎪⎧i1Δ=R12u12Δ−R31u31Δi2Δ=R23u23Δ−R12u12Δi3Δ=R31u31Δ−R23u23Δ
Y 形 联 结 : 用 电 流 表 示 电 压 { u 12 Y = R 1 i 1 Y − R 2 i 2 Y u 23 Y = R 2 i 2 Y − R 3 i 3 Y u 31 Y = R 3 i 3 Y − R 1 i 1 Y i 1 Y + i 2 Y + i 3 Y = 0 Y形联结:用电流表示电压\begin{cases} u_{12Y}=R_1i_{1Y}-R_2i_{2Y}\\ u_{23Y}=R_2i_{2Y}-R_3i_{3Y}\\ u_{31Y}=R_3i_{3Y}-R_1i_{1Y}\\ i_{1Y}+i_{2Y}+i_{3Y}=0 \end{cases} Y形联结:用电流表示电压⎩⎪⎪⎪⎨⎪⎪⎪⎧u12Y=R1i1Y−R2i2Yu23Y=R2i2Y−R3i3Yu31Y=R3i3Y−R1i1Yi1Y+i2Y+i3Y=0
Y 转 Δ 的 转 变 条 件 为 { R 12 = R 1 + R 2 + R 1 R 2 R 3 R 23 = R 2 + R 3 + R 2 R 3 R 1 R 31 = R 3 + R 1 + R 3 R 1 R 2 Y转Δ的转变条件为\begin{cases} R_{12}=R_1+R_2+\frac{R_1R_2}{R_3}\\ R_{23}=R_2+R_3+\frac{R_2R_3}{R_1}\\ R_{31}=R_3+R_1+\frac{R_3R_1}{R_2} \end{cases} Y转Δ的转变条件为⎩⎪⎨⎪⎧R12=R1+R2+R3R1R2R23=R2+R3+R1R2R3R31=R3+R1+R2R3R1
Δ 转 Y 的 转 变 条 件 为 { R 1 = R 12 R 31 R 12 + R 23 + R 31 R 2 = R 23 R 12 R 12 + R 23 + R 31 R 3 = R 31 R 23 R 12 + R 23 + R 31 Δ转Y的转变条件为\begin{cases} R_{1}=\frac{R_{12}R_{31}}{R_{12}+R_{23}+R_{31}}\\ R_{2}=\frac{R_{23}R_{12}}{R_{12}+R_{23}+R_{31}}\\ R_{3}=\frac{R_{31}R_{23}}{R_{12}+R_{23}+R_{31}} \end{cases} Δ转Y的转变条件为⎩⎪⎨⎪⎧R1=R12+R23+R31R12R31R2=R12+R23+R31R23R12R3=R12+R23+R31R31R23


2-5 电压源、电流源的串联和并联
理想电压源的串联和并联
串 联 : u = u 1 + u 2 + . . . + u n = ∑ k = 1 n u S k 串联: u=u_1+u_2+...+u_n=\sum_{k=1}^{n}u_{Sk} 串联:u=u1+u2+...+un=k=1∑nuSk
相 同 的 理 想 电 压 源 才 能 并 联 , 电 源 中 的 电 流 不 确 定 。 相同的理想电压源才能并联,电源中的电流不确定。 相同的理想电压源才能并联,电源中的电流不确定。
理想电流源的串联和并联
并 联 : i = i 1 + i 2 + . . . + i n = ∑ k = 1 n i S k 并联: i=i_1+i_2+...+i_n=\sum_{k=1}^{n}i_{Sk} 并联:i=i1+i2+...+in=k=1∑niSk
相 同 的 理 想 电 流 源 才 能 串 联 , 每 个 电 流 源 的 端 电 压 不 能 确 定 。 相同的理想电流源才能串联, 每个电流源的端电压不能确定。 相同的理想电流源才能串联,每个电流源的端电压不能确定。
2-6 实际电源的两种模型及其等效变换
I s = u s R s ( R 不 变 ) I_s=\frac{u_s}{R_s} \ \ \ \ \ \ \ (R不变) Is=Rsus (R不变)
2-7 输入电阻
如果一端口内部仅含电阻,则应用电阻的串、并联和-Y变换等方法求它的等效电阻。
对含有受控源和电阻的二端电路,用电压、电流法求输入电阻,即在端口加电压源,求得电流,或在端口加电流源,求得电压,得其比值。
第三章 电阻电路的一般分析
3-2 KCL和KVL的独立方程数

K C L { 1 i 1 − i 4 − i 6 = 0 2 − i 1 − i 2 + i 3 = 0 3 i 2 + i 5 + i 6 = 0 4 − i 3 + i 4 − i 5 = 0 KCL\begin{cases} 1\ \ \ \ i_1-i_4-i_6=0\\ 2\ \ \ \ -i_1-i_2+i_3=0\\ 3\ \ \ \ i_2+i_5+i_6=0\\ 4\ \ \ \ -i_3+i_4-i_5=0 \end{cases} KCL⎩⎪⎪⎪⎨⎪⎪⎪⎧1 i1−i4−i6=02 −i1−i2+i3=03 i2+i5+i6=04 −i3+i4−i5=0
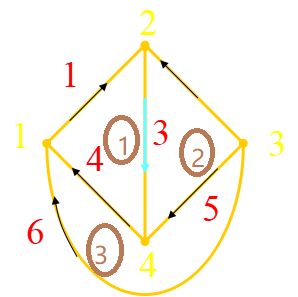
K V L { 1 u 1 + u 3 + u 4 = 0 2 u 2 + u 3 − u 5 = 0 3 u 4 + u 5 − u 6 = 0 KVL\begin{cases} 1\ \ \ \ \ \ \ u_1+u_3+u_4=0\\ 2\ \ \ \ \ \ \ u_2+u_3-u_5=0\\ 3\ \ \ \ \ \ \ u_4+u_5-u_6=0 \end{cases} KVL⎩⎪⎨⎪⎧1 u1+u3+u4=02 u2+u3−u5=03 u4+u5−u6=0
3-3 支路电流法
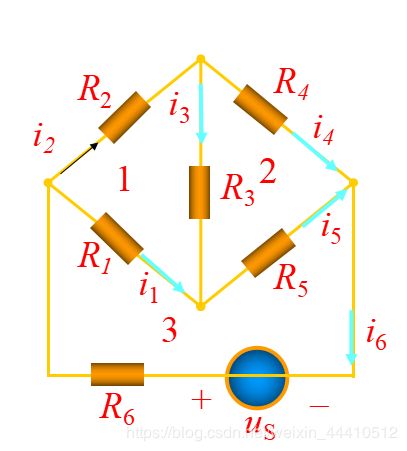
K C L { 1 i 1 + i 2 − i 6 = 0 2 − i 2 + i 3 + i 4 = 0 3 − i 4 − i 5 + i 6 = 0 KCL\begin{cases} 1\ \ \ \ \ \ \ i_1+i_2-i_6=0\\ 2\ \ \ \ \ \ \ -i_2+i_3+i_4=0\\ 3\ \ \ \ \ \ \ -i_4-i_5+i_6=0 \end{cases} KCL⎩⎪⎨⎪⎧1 i1+i2−i6=02 −i2+i3+i4=03 −i4−i5+i6=0
K V L { 1 u 2 + u 3 − u 1 = 0 2 u 4 − u 5 − u 3 = 0 3 u 1 + u 5 + u 6 − u s = 0 KVL\begin{cases} 1\ \ \ \ \ \ \ u_2+u_3-u_1=0\\ 2\ \ \ \ \ \ \ u_4-u_5-u_3=0\\ 3\ \ \ \ \ \ \ u_1+u_5+u_6-u_s=0 \end{cases} KVL⎩⎪⎨⎪⎧1 u2+u3−u1=02 u4−u5−u3=03 u1+u5+u6−us=0
{ R 2 i 2 + R 3 i 3 − R 1 i 1 = 0 R 4 i 4 − R 5 i 5 − R 3 i 3 = 0 R 1 i 1 + R 5 i 5 + R 6 i 6 = 0 \begin{cases} R_2i_2+R_3i_3-R_1i_1=0\\ R_4i_4-R_5i_5-R_3i_3=0\\ R_1i_1+R_5i_5+R_6i_6=0 \end{cases} ⎩⎪⎨⎪⎧R2i2+R3i3−R1i1=0R4i4−R5i5−R3i3=0R1i1+R5i5+R6i6=0
支路电流法的一般步骤:
标定各支路电流(电压)的参考方向。
选定 n–1个结点,列写其KCL方程。
选定 b –( n –1)个独立回路,指定回路绕行方向,结合KVL和支路方程
求解上述方程,得到b个支路电流。
进一步计算支路电压和进行其他分析。
3-4 网孔电流法
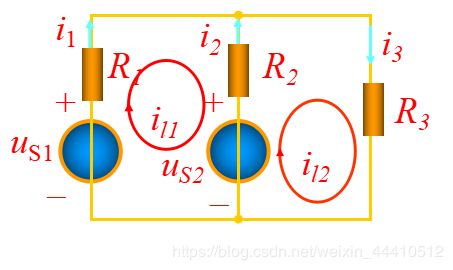
{ ( R 1 + R 2 ) i 11 − R 2 i 12 = u s 1 − u s 2 ( R 2 + R 3 ) i 12 − R 2 i 1 = u s 2 \begin{cases} (R_1+R_2)i_{11}-R_2i_{12}=u_{s1}-u_{s2}\\ (R_2+R_3)i_{12}-R_2i_1=u_{s2} \end{cases} {(R1+R2)i11−R2i12=us1−us2(R2+R3)i12−R2i1=us2
网孔电流法的一般步骤:
选网孔为独立回路,并确定其绕行方向。
以网孔电流为未知量,列写其KVL方程。
求解上述方程,得到 l 个网孔电流。
求各支路电流。
其他分析。
3-5 回路电流法
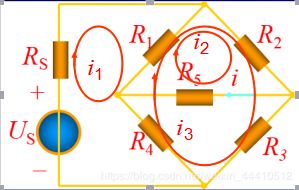
( R s + R 1 + R 4 ) i 1 − R 1 i 2 − ( R 1 + R 4 ) i 3 = U s (R_s+R_1+R_4)i_1-R_1i_2-(R_1+R_4)i_3=U_s (Rs+R1+R4)i1−R1i2−(R1+R4)i3=Us
( R 1 + R 2 + R 5 ) i 2 − R 1 i 1 + ( R 1 + R 2 ) i 3 = 0 (R_1+R_2+R_5)i_2-R_1i_1+(R_1+R_2)i_3=0 (R1+R2+R5)i2−R1i1+(R1+R2)i3=0
( R 1 + R 2 + R 3 + R 4 ) i 3 − ( R 1 + R 4 ) i 1 + ( R 1 + R 2 ) i 2 = 0 (R_1+R_2+R_3+R_4)i_3-(R_1+R_4)i_1+(R_1+R_2)i_2=0 (R1+R2+R3+R4)i3−(R1+R4)i1+(R1+R2)i2=0
i = i 2 i=i_2 i=i2
回路法的一般步骤:
选定l=b-(n-1)个独立回路,并确定其绕行方向。
对l 个独立回路,以回路电流为未知量,列写其KVL方程。
求解上述方程,得到 l 个回路电流。
求各支路电流。
3-6 结点电压法
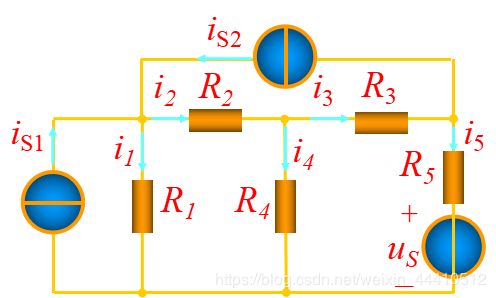
( 1 R 1 + 1 R 2 ) u n 1 − ( 1 R 2 ) u n 2 = i s 1 + i s 2 (\frac{1}{R_1}+\frac{1}{R_2})u_{n1}-(\frac{1}{R_2})u_{n2}=i_{s1}+i_{s2} (R11+R21)un1−(R21)un2=is1+is2
( 1 R 2 + 1 R 3 + 1 R 4 ) u n 2 − 1 R 2 u n 1 − 1 R 3 u n 3 = 0 (\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4})u_{n2}-\frac{1}{R_2}u_{n1}-\frac{1}{R_3}u_{n3}=0 (R21+R31+R41)un2−R21un1−R31un3=0
( 1 R 3 + 1 R 5 ) u n 3 − ( 1 R 3 ) u n 2 = − i s 2 + u s R 5 (\frac{1}{R_3}+\frac{1}{R_5})u_{n3}-(\frac{1}{R_3})u_{n2}=-i_{s2}+\frac{u_s}{R_5} (R31+R51)un3−(R31)un2=−is2+R5us
结点法的一般步骤:
(1)选定参考结点,标定n-1个独立结点。
(2)对n-1个独立结点,以结点电压为未知量,列写其KCL方程。
(3)求解上述方程,得到n-1个结点电压。
(4)通过结点电压求各支路电流。
第四章 电路定理
4-1 叠加定理
在线性电路中,任一支路的电流(或电压)可以看成是电路中每一个独立电源单独作用于电路时,在该支路产生的电流(或电压)的代数和。
叠加定理只适用于线性电路。
一个电源作用,其余电源为零。
电压源为零 —— 短路。
电流源为零 —— 开路。
功率不能叠加(功率为电压和电流的乘积,为电源的二次函数)。
u, i叠加时要注意各分量的参考方向。
含受控源(线性)电路亦可叠加,但受控源应始终保留。
齐性原理
线性电路中,所有激励(独立电源)都增大(或减小)同样的倍数,则电路中响应(电压或电流)也增大(或减小)同样的倍数。
4-2 替代定理
对于给定的任意一个电路,若某一支路电压为uk、电流为ik,那么这条支路就可以用一个电压等于uk的独立电压源,
或者用一个电流等于ik的独立电流源,或用R=uk/ik的电阻来替代,替代后电路中全部电压和电流均保持原有值(解答唯一)。
替代定理既适用于线性电路,也适用于非线性电路。
替代后电路必须有唯一解。
无电压源回路;
无电流源结点(含广义结点)。
替代后其余支路及参数不能改变。
4-3 戴维宁定理和诺顿定理
戴维宁定理
任何一个线性含源一端口网络,对外电路来说,总可以用一个电压源和电阻的串联组合来等效置换;
此电压源的电压等于外电路断开时端口处的开路电压uoc,而电阻等于一端口的输入电阻(或等效电阻)Req。
应用
开路电压uoc 的计算
戴维宁等效电路中电压源电压等于将外电路断开时的开路电压uoc,电压源方向与所求开路电压方向有关。
计算uoc的方法视电路形式选择前面学过的任意方法,使易于计算。
等效电阻的计算
等效电阻为将一端口网络内部独立电源全部置零(电压源短路,电流源开路)后,所得不含独立源一端口网络的输入电阻。
常用下列方法计算:
当网络内部不含有受控源时可采用电阻串并联和-Y互换的方法计算等效电阻。
外加电源法(加电压求电流或加电流求电压)。
开路电压,短路电流法。
注意
外电路可以是任意的线性或非线性电路,外电路发生改变时,含源一端口网络的等效电路不变(伏安特性等效)。
当一端口内部含有受控源时,控制电路与受控源必须包含在被化简的同一部分电路中。
诺顿定理
任何一个含源线性一端口电路,对外电路来说,可以用一个电流源和电阻的并联组合来等效置换;
电流源的电流等于该一端口的短路电流,电阻等于该一端口的输入电阻。
一般情况,诺顿等效电路可由戴维宁等效电路经电源等效变换得到。诺顿等效电路可采用与戴维宁定理类似的方法证明。
4-4 最大功率传输定理
P = R L ( u o c ( R e q + R L ) ) 2 P=R_L(\ \frac{u_{oc}}{(R_{eq}+R_L)}\ )^2 P=RL( (Req+RL)uoc )2
当 R L = = R e q 时 P m a x = u o c 2 4 R e q 当 \ \ \ R_L==R_{eq} \ \ 时\ \ \ \ P_{max}=\frac{u_{oc}^2}{4R_{eq}} 当 RL==Req 时 Pmax=4Requoc2
注意
最大功率传输定理用于一端口电路给定,负载电阻可调的情况。
一端口的等效电阻消耗的功率一般并不等于端口内部消耗的功率,因此当负载获取最大功率时,电路的传输效率并不一定是50%。
计算最大功率问题结合应用戴维宁定理或诺顿定理最方便。