同时考虑距离因素和分布因素的多样化近邻图DPG——TKDE顶刊论文阅读笔记
博客地址: https://mzwang.top/
论文题目
Approximate Nearest Neighbor Search on High Dimensional Data — Experiments, Analyses, and Improvement
相关信息
作者与单位
Wen Li([email protected]); Nanjing Audit University; University of Technology Sydney;
Ying Zhang([email protected]); University of Technology Sydney;
Yifang Sun([email protected]); The University of New South Wales;
Wei Wang([email protected]); The University of New South Wales;
Mingjie Li([email protected]); University of Technology Sydney;
Wenjie Zhang([email protected]); The University of New South Wales
Xuemin Lin([email protected]); The University of New South Wales
出处与时间
Transactions on Knowledge and Data Engineering(2019数据库/数据挖掘/内容检索A类期刊); 2019
作者拟解决的主要问题
尽管目前已有很多近似最近邻算法,但是它们的性能没有得到全面的评估和分析。本文对各类近似最近邻算法进行了一个全面的评估,这样做的目的有以下三点:
- 各个领域的算法和数据集可能会"并行提出"。某一领域的解决方案可能已在另一领域中存在,而不必重复开发。而且,不同领域的算法很少能放在一起比较的。
- 忽略了评估标准和设置。一个近似最近邻算法可从各个角度来评估。比如,搜索时间、搜索质量、索引尺寸、可扩展性(关于数据集的规模和维数)、鲁棒性(数据集、查询负载和参数设置)、可更新性,调参工作量等。
- 现存结果的差异。同一个算法不同的实施结果差别很大,我们需要一个一致性的比较结果。
而且,通过实验和分析,本文提出了一种新的基于近邻图的近似最近邻搜索算法——DPG。该方法在构建k近邻图时同时考虑了数据点的距离和数据点的分布,这不同于之前的NN-Descent和Wang提出的方法。
论文主要研究内容
- 对现存一些主要的近似最近邻算法做一个全面的评估。
- 分析造成各种算法在不同情况下的优劣的原因。
- 构建一个更有效的基于近邻图的近似最近邻算法。
论文使用的方法
动机案例
近邻图的构建一般只考虑数据点与它的邻居点的距离。但是,本文不仅考虑这一点,它还考虑邻居点的分布,为什么要这样呢?请看图1。

图1中, a 3 a_3 a3 和 a 4 a_4 a4 是 p p p 的最近邻,在2-NN图中,如果查询点为 q q q ,搜索执行到 p p p 时是无法继续收敛到 q q q 的最近邻点 b b b 的。 a 1 a_1 a1 , a 2 a_2 a2 , a 3 a_3 a3 , a 4 a_4 a4 之间离得很近,可以认为它们处于同一个集簇,这个时候 a 3 a_3 a3 和 a 4 a_4 a4 都在 p p p 的邻居列表中其实作用不大。本文在连边时不仅考虑距离的远近,而且还考虑方向的多样性,从而构建一个多样化近邻图(Diversified Proximity Graph, DPG)。在图1中,如果 p p p 的邻居是 a 3 a_3 a3 和 b b b ,那将更有意义。
假设现在有向边 ⟨ p , a 4 ⟩ \langle p, a_4 \rangle ⟨p,a4⟩ 已经没了,现在 p p p 的邻居是 a 3 a_3 a3 和 b b b 。另一个问题又发生了, p p p 只有出边而没有入边,因为 p p p 周围的点距 p p p 都挺远的, p p p 不是这些点前两个最近邻点。这将导致 p p p 左右两边的两个聚簇其实是不连通的,有研究表明,这一现象在高维数据中更普遍。因此,本文在连边时添加的边是双向边。
DPG的构建过程
给定点 p p p ,它的最近邻列表为 L L L ,在 p p p 的最近邻列表中的两点 x x x 和 y y y 的相似性定义为角度 ∡ x p y \measuredangle xpy ∡xpy ,表示为 θ ( x , y ) \theta (x,y) θ(x,y) 。我们的目标就是在 L L L 中找一个子集 S S S ,其中 ∣ S ∣ = k \lvert S \rvert = k ∣S∣=k ,使得在 S S S 中,任意两点的夹角的平均值最大,这样的 S S S 中的点与 p p p 连边。
核心选边过程: S S S 初始化为 L L L 中距 p p p 最近的点,接下来就是 k − 1 k-1 k−1 次迭代选边过程,此过程同时考虑距离和分布两个因素。在每一次迭代,从集合 L ∖ S L \setminus S L∖S 中移出一个点到 S S S 中,并且移出的这个点是使 S S S 中各点对之间的夹角的平均值最小的点(类似于经典的求最短路径的算法)。这个过程的时间复杂度为 O ( k 2 K n ) O(k^2 K n) O(k2Kn) 。
时间复杂度推导过程: 现数据集中一共有 n n n 个点,给其中一个点 p p p 选边,它的最近邻列表 L L L 中有 K K K 个点,表示为: v 1 , v 2 , ⋯ , v K v_1, v_2, \cdots, v_K v1,v2,⋯,vK ,假设它们已按距 p p p 的距离升序排好序。开始时先将 v 1 v_1 v1 (作为 s 1 s_1 s1)加入集合 S S S ,接着,从 L L L 中剩下的 K − 1 K-1 K−1 个点里面选一个 s 2 s_2 s2 ,使得 ∡ s 1 p s 2 \measuredangle s_1 p s_2 ∡s1ps2 最大,因此需要 K − 1 K-1 K−1 次计算。 s 2 s_2 s2 找到后, L L L 里面还剩下 K − 2 K-2 K−2 个点,从其中选一个 s 3 s_3 s3 ,使得 ∡ s 1 p s 3 \measuredangle s_1 p s_3 ∡s1ps3 与 ∡ s 2 p s 3 \measuredangle s_2 p s_3 ∡s2ps3 之和最大,因此需要 2 ( K − 2 ) 2(K-2) 2(K−2) 次计算,……
因此,从 L L L 中选择 k k k 个点到 S S S 中,需要的总计算次数为
∑ i = 1 k − 1 i ( k − i ) \sum_{i=1}^{k-1} i(k-i) i=1∑k−1i(k−i)
化简可得
k ( k − 1 ) 2 K − k ( k − 1 ) ( 2 k − 1 ) 6 \frac{k(k-1)}{2} K - \frac{k(k-1)(2k-1)}{6} 2k(k−1)K−6k(k−1)(2k−1)
即为
O ( k 2 K ) − O ( k 3 ) = O ( k 2 K ) O(k^2 K) - O(k^3)=O(k^2 K) O(k2K)−O(k3)=O(k2K)
因此,给所有点选边的理论时间复杂度为 O ( k 2 K n ) O(k^2 K n) O(k2Kn) 。
K K K 值是权衡距离因素和分布因素的一个重要参数,作者在实验中得出, K = 2 k K=2k K=2k 时能够实现最好的性能。
在实际实施时,本文并不是完全按照上述描述来执行的,因为上述过程的时间复杂度还是挺高的,作者通过对上述过程近似实施了一个简化版本,它的时间复杂度为 O ( K 2 n ) O(K^2 n) O(K2n) 。
简化版本选边过程: 给 p p p 选边时,为它的 K K K 近邻列表 L L L 中的每个点都设置一个计数器。比如,对于点对 u u u 和 v v v,如果 v v v 到 u u u 的距离小于 v v v 到 p p p 的距离,则 v v v 的计数器加一,对 L L L 中的任意两个点都执行上述操作。之后,保留 k k k 个计数器的值最小的点作为 p p p 的邻居。这样做的直觉是: 对于点 x x x,如果有很多点与之处于同一方向,则 x x x 的计数器的值就会很大。这个简化版本的选边与HNSW有一点点类似的。
论文的创新点
- 实践了更全面的对近似最近邻搜索算法进行评估的方法;
- 近邻图构建时把选边过程的约束总结为两个因素,并分析说明数据分布因素对构建一个面向近似最近邻搜索的近邻图的重要性;
- 提出了按角度选边这种数据分布因素的具体实施方式;
- 提出了能够和按角度选边实现近似效果的简化版本实施数据分布因素的选边方式。
论文的结论
先看一个搜索性能图
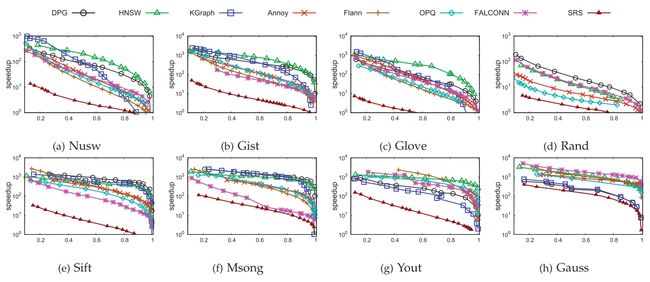
由图2可见,大部分情况下,HNSW的搜索性能是最优的,本文提出的DPG只在少数情况下是最优。而且,HNSW的性能在各种数据集下是最稳定的。因此,整体而言,HNSW的选边策略还是更好一些,它的分层结构可能也做出了一些贡献。
另一方面,DPG性能普遍优于KGraph,特别在召回率区域,这说明了考虑数据分布因素的必要性。
我的观点或思考
要构建一个面向相似性搜索的近邻图,只考虑距离因素是不行的,如何实施一个数据分布因素是一个值得考虑的问题。
近邻图构建的常用思路: 先提出抽象构建思路,这个过程一般可以很容易的符号化描述,一些性质也可严密推导,但一般其构建的时间复杂度较高,因此,会有一个近似的版本,近似版本可与抽象版本实现非常接近的效果(或者稍微差一点),而且近似版本一般还可显著降低构建的时间复杂度。