redis中sortset跳表数据结构

 转自

http://www.cnblogs.com/steve-jiang/p/9206589.html

 

跳跃列表是在很多应用中有可能替代平衡树而作为实现方法的一种数据结构。跳跃列表的算法有同平衡树一样的渐进的预期时间边界，并且更简单、更快速和使用更少的空间。----by 发明者

像是redis中有序集合就使用到了跳跃表。

场景：商品总数量有几十万件，对应数据库商品表的几十万条记录。需要根据不同字段正序或者倒叙做精确或全量查询，而且性能有硬性要求。

 

如果是按照商品名称精确查询还好办，可以直接从数据库查出来，最多也就上百条记录。

如果是没有商品名称的全量查询怎么办？总不可能把数据库里的所有记录全查出来吧，而且还要支持不同字段的排序。

所以，只能提前在内存中存储有序的全量商品集合，每一种排序方式都保存成独立的集合，每次请求的时候按照请求的排序种类，返回对应的集合。

• 比如按价格字段排序的集合：
• 比如按销量字段排序的集合：

商品列表是线性的，最容易表达线性结构的自然是数组和链表。可是，无论是数组还是链表，在插入新商品的时候，都会存在性能问题。

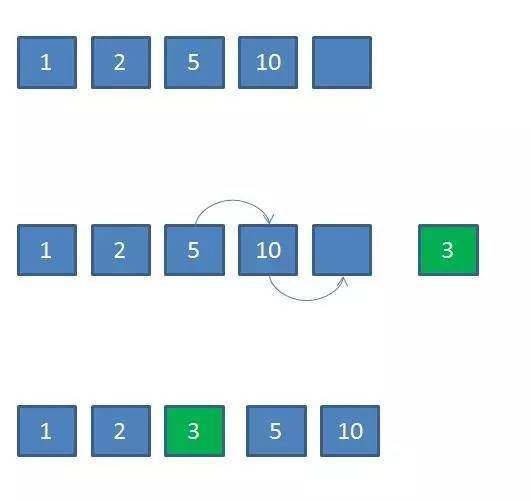
按照商品等级排序的集合为例，如果使用数组，插入新商品的方式如下：

如果要插入一个价格是3的商品，首先要知道这个商品应该插入的位置。使用二分查找可以最快定位，这一步时间复杂度是O（logN）。

插入过程中，原数组中所有大于3的商品都要右移，这一步时间复杂度是O（N）。所以总体时间复杂度是O（N）。

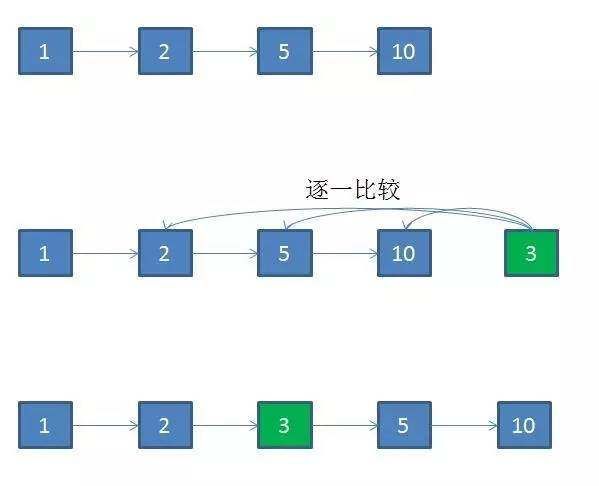
如果使用链表，插入新商品的方式如下：

 

 

 

 

如果要插入一个价格是3的商品，首先要知道这个商品应该插入的位置。链表无法使用二分查找，只能和原链表中的节点逐一比较大小来确定位置。这一步的时间复杂度是O（N）。

插入的过程倒是很容易，直接改变节点指针的目标，时间复杂度O（1）。因此总体的时间复杂度也是O（N）。

这对于拥有几十万商品的集合来说，这两种方法显然都太慢了。

 

因此引入一种不同的数据结构----跳跃表

首先，应该要了解跳跃表的性质；

• 由很多层结构组成；
• 每一层都是一个有序的链表，排列顺序为由高层到底层，都至少包含两个链表节点，分别是前面的head节点和后面的nil节点；
• 最底层的链表包含了所有的元素；
• 如果一个元素出现在某一层的链表中，那么在该层之下的链表也全都会出现（上一层的元素是当前层的元素的子集）；
• 链表中的每个节点都包含两个指针，一个指向同一层的下一个链表节点，另一个指向下一层的同一个链表节点；

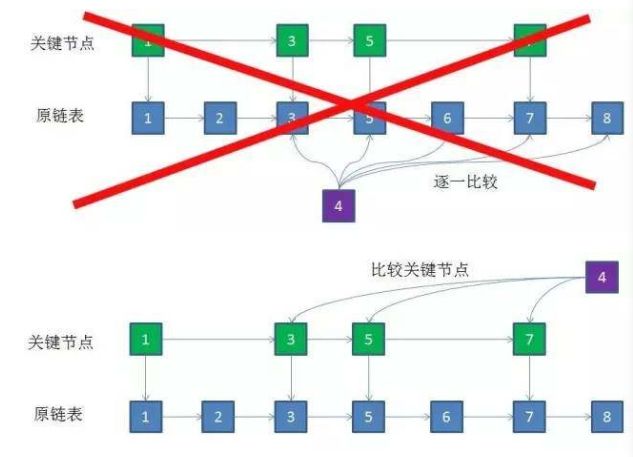
因此在前文中的商品列表排序中，可以取出若干关键节点，在新节点插入时先去比较关键节点，逐层下沉，最终在原链表中插入。这样，比较的次数下降了一半，节点数量少的情况下效果不明显，但在1w甚至10w个节点的链表下，性能的提升会非常明显。

 

 

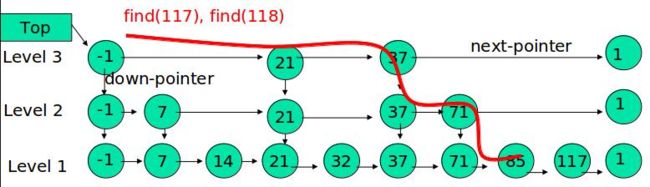
搜索：

 

 

 

其基本原理就是从最高层的链表节点（关 键节点）开始，如果比当前节点要大和比当前层的下一个节点要小，那么则往下找，也就是和当前层的下一层的节点的下一个节点进行比较，以此类推，一直找到最底层的最后一个节点，如果找到则返回，反之则返回空。

 

 

 1 find(x)   
 2 {  
 3     p = top;  
 4     while (1) {  
 5         while (p->next->key < x)  
 6             p = p->next;  
 7         if (p->down == NULL)   
 8             return p->next;  
 9         p = p->down;  
10     }  
11 } 

插入节点 ：

既然要插入，首先需要确定插入的层数，这里有不一样的方法。1. 看到一些博客写的是抛硬币，只要是正面就累加，直到遇见反面才停止，最后记录正面的次数并将其作为要添加新元素的层；2. 还有就是一些博客里面写的统计概率，先给定一个概率p，产生一个0到1之间的随机数，如果这个随机数小于p，则将高度加1，直到产生的随机数大于概率p才停止，根据给出的结论，当概率为1/2或者是1/4的时候，整体的性能会比较好（其实当p为1/2的时候，也就是抛硬币的方法）。

当确定好要插入的层数以后，则需要将元素都插入到从最底层到第k层

抛硬币法：

 

 

新节点和各层索引节点逐一比较，确定原链表的插入位置。O（logN）

把索引插入到原链表。O（1）

利用抛硬币的随机方式，决定新节点是否提升为上一级索引。结果为“正”则提升并继续抛硬币，结果为“负”则停止。O（logN）

总体上，跳跃表插入操作的时间复杂度是O（logN），而这种数据结构所占空间是2N，既空间复杂度是 O（N）。

删除节点

在各个层中找到包含指定值的节点，然后将节点从链表中删除即可，如果删除以后只剩下头尾两个节点，则删除这一层。

 

 

自上而下，查找第一次出现节点的索引，并逐层找到每一层对应的节点。O（logN）

删除每一层查找到的节点，如果该层只剩下1个节点，删除整个一层（原链表除外）。O（logN）

总体上，跳跃表删除操作的时间复杂度是O（logN）。

 

代码示例：

 

 

 1 /***************************  SkipList.java  *********************/
 2 
 3 import java.util.Random;
 4 
 5 public class SkipList> {
 6     private int maxLevel;
 7     private SkipListNode[] root;
 8     private int[] powers;
 9     private Random rd = new Random();
10     SkipList() {
11         this(4);
12     }
13     SkipList(int i) {
14         maxLevel = i;
15         root = new SkipListNode[maxLevel];
16         powers = new int[maxLevel];
17         for (int j = 0; j < maxLevel; j++)
18             root[j] = null;
19         choosePowers();
20     }
21     public boolean isEmpty() {
22         return root[0] == null;
23     }
24     public void choosePowers() {
25         powers[maxLevel-1] = (2 << (maxLevel-1)) - 1;    // 2^maxLevel - 1
26         for (int i = maxLevel - 2, j = 0; i >= 0; i--, j++)
27            powers[i] = powers[i+1] - (2 << j);           // 2^(j+1)
28     }
29     public int chooseLevel() {
30         int i, r = Math.abs(rd.nextInt()) % powers[maxLevel-1] + 1;
31         for (i = 1; i < maxLevel; i++)
32             if (r < powers[i])
33                 return i-1; // return a level < the highest level;
34         return i-1;         // return the highest level;
35     }
36     // make sure (with isEmpty()) that search() is called for a nonempty list;
37     public T search(T key) { 
38         int lvl;
39         SkipListNode prev, curr;            // find the highest nonnull
40         for (lvl = maxLevel-1; lvl >= 0 && root[lvl] == null; lvl--); // level;
41         prev = curr = root[lvl];
42         while (true) {
43             if (key.equals(curr.key))          // success if equal;
44                  return curr.key;
45             else if (key.compareTo(curr.key) < 0) { // if smaller, go down,
46                  if (lvl == 0)                 // if possible
47                       return null;      
48                  else if (curr == root[lvl])   // by one level
49                       curr = root[--lvl];      // starting from the
50                  else curr = prev.next[--lvl]; // predecessor which
51             }                                  // can be the root;
52             else {                             // if greater,
53                  prev = curr;                  // go to the next
54                  if (curr.next[lvl] != null)   // non-null node
55                       curr = curr.next[lvl];   // on the same level
56                  else {                        // or to a list on a lower level;
57                       for (lvl--; lvl >= 0 && curr.next[lvl] == null; lvl--);
58                       if (lvl >= 0)
59                            curr = curr.next[lvl];
60                       else return null;
61                  }
62             }
63         }
64     }
65     public void insert(T key) {
66         SkipListNode[] curr = new SkipListNode[maxLevel];
67         SkipListNode[] prev = new SkipListNode[maxLevel];
68         SkipListNode newNode;
69         int lvl, i;
70         curr[maxLevel-1] = root[maxLevel-1];
71         prev[maxLevel-1] = null;
72         for (lvl = maxLevel - 1; lvl >= 0; lvl--) {
73             while (curr[lvl] != null && curr[lvl].key.compareTo(key) < 0) { 
74                 prev[lvl] = curr[lvl];           // go to the next
75                 curr[lvl] = curr[lvl].next[lvl]; // if smaller;
76             }
77             if (curr[lvl] != null && key.equals(curr[lvl].key)) // don't 
78                 return;                          // include duplicates;
79             if (lvl > 0)                         // go one level down
80                 if (prev[lvl] == null) {         // if not the lowest
81                       curr[lvl-1] = root[lvl-1]; // level, using a link
82                       prev[lvl-1] = null;        // either from the root
83                 }
84                 else {                           // or from the predecessor;
85                      curr[lvl-1] = prev[lvl].next[lvl-1];
86                      prev[lvl-1] = prev[lvl];
87                 }
88         }
89         lvl = chooseLevel();                // generate randomly level 
90         newNode = new SkipListNode(key,lvl+1); // for newNode;
91         for (i = 0; i <= lvl; i++) {        // initialize next fields of
92             newNode.next[i] = curr[i];      // newNode and reset to newNode
93             if (prev[i] == null)            // either fields of the root
94                  root[i] = newNode;         // or next fields of newNode's
95             else prev[i].next[i] = newNode; // predecessors;
96         }
97     }
98 }

 

有的时候跳跃表常用来代替红黑树，因为跳跃表在维持结构平衡时成本较低，完全靠随机，而红黑树这一类查找树每一次添加删除后都需要rebalance。