机器学习——条件随机场CRF
看到条件随机场的时候想到了贝叶斯网... ...当初匆匆略过贝叶斯网就觉得，啊呀，用图和边表示这个随机变量之间是否有联系真的很方便啊。后面就看到了条件随机场。
如果接触过deeplab的还会记得有个全连接条件随机场，用于精细分割的结果，全连接条件随机场和条件随机场的关系又是什么？
（回过头看自己的博客，目前主要是为了记录给自己看的，等忙过秋招，就好好倒腾一下把）
1 如何引入条件随机场（条件随机场是什么鬼？）
情景：卷子：请问，何事秋风悲画扇？到底是因为什么事悲画扇呢？ 我（一脸懵逼... ...）：这个。。突然想到语文老师经常说的，一定要结合上下文，于是我回过头看那首诗句：
人生若只如初见，何事秋风悲画扇？
等闲变却故人心，却道故人心易变。
答：主人公呢是因为自己喜欢的人不喜欢自己了而伤心呢。
对的，你已经使用了条件随机场的思想，结合上下文的信息作出一些判断（所以，语文才是始终贯彻条件随机场啊）。
字面理解，条件嘛，肯定是会有些前提条件，然后让你求个条件概率什么的。场？联想到电场磁场，就两个或多个电极之间用虚线交流着...（脑补高中物理课本）。条件随机场就是给定一组输入随机变量条件下另一组输出随机变量的条件概率分布模型，其特点就是输出随机变量构成马尔科夫随机场。
嗯？！什么是马尔科夫随机场，为什么要来这个马场？
这个，让数学老师来讲吧~语文老师下线。
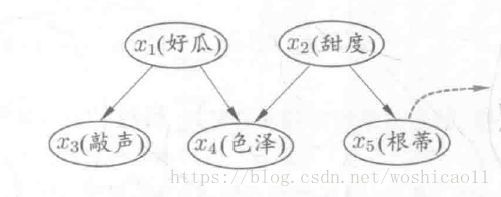
还记得朴素贝叶斯吗？我们需要求P(Y|x1,x2,...,xn)，但这个条件概率太难求了，因为如果特征之间独立还好办，直接相乘，但如果不独立，那你还需要x之间的关系。于是不朴素的劳模贝叶斯就想到了一个好办法，画图来刻画属性之间的关系：
所以，图用来刻画输入和输出的关系是非常方便的选择。节点表示属性，节点之间的有没有关系可以用线刻画。而马尔科夫随机场呢，它是满足一定条件的这么个图，因为它某些特性，简化了计算量。ok，现在看看马场是什么？
2 马尔科夫随机场
（联想到课本的电场磁场，就是几个点之间用虚线交流着，就明白为什么会定义为随机场了）
从数学上我们去定义这个模型，三要素，Graph，Node，Edge，用图Graph表示概率分布，Graph的节点Node表示随机变量，Graph的边Edge表示随机变量之间的依赖关系（不能反映多亲的依赖关系）
当这个Graph满足以下特性：
成对马尔可夫性
局部马尔可夫性
全局马尔可夫性
我们就成为这个概率图是马尔科夫随机场。而这三个特性是等价的，满足其中任一个，其它两个也必定满足。
解释一下这三个特性。
成对马尔可夫性，对，P(Yu,Yv|Yo)=P(Yu|Yo)P(Yv|Yo)
局部马尔可夫性，局，P(Yv|Yw)=P(Yu|Yw,Yo)
全局马尔可夫性，全，P(YA,YB|YC)=P(YA|YC)P(YB|YC)
而马尔科夫场有个定理，就是：
C为这个场的最大团，Yc表示这个团中的随机变量们，也就是马场的联合概率分布P（Y）可写作图中所有最大团C上的函数乘机的形式。
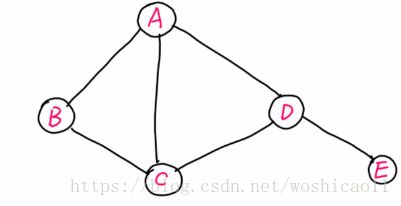
什么是最大团？
团：任意两个节点均有边连接的节点子集称为团，若这个团不能再加进任何一个节点使其成为一个更大的团，则为最大团。
这个定理有什么好处呢？当然，对于这种概率模型，学习的时候，要么最大化条件概率（如LR）要么最大化后验概率（朴素贝叶斯），这个定理肯定是能简化联合概率的求解。
3 条件随机场（条件）
条件随机场的数学模型：
对任意节点v成立。
表示出来v之外的所有节点w，
与节点v有边连接的所以节点w。
以下我们具体看一下特殊的条件随机场——线性链条件随机场：Y为线性链表示的随机变量，线性链如下图：
用公式表示：
这里最大团就是两个相邻的点：{Y1,Y2}，{Y2,Y3}，{Y3,Y4}，...，{Yn-1,Yn}，根据因子分解式：
那这个
如何确定呢？在此要介绍以下特征函数。
tk是定义在边上的特征函数，称为转移特征，依赖于当前和前一个位置，sl是定义在节点上的特征函数，称为状态特征，依赖于当前位置。通常tk和sl取值为1和0，满足条件时为1，否则为0。
这里可能会有疑问，i可以理解，为什么还有k呢？因为如果tk是定义在边上的特征函数，如果是线性链，不是两个节点只有一条边吗？
这个解释一下，比如，状态1-->状态2，状态1是高兴，状态2 取值可以是，高兴，也可以是不高兴，则t1（高兴，高兴，x，i=2）和t2（不高兴，高兴，x，i=2），这两个t前面的λ是不一样的。
线性链条件随机场也是对数线性模型。
嗯tk和sl可以统一用F(yi-1，yi，x，i)表示，以上可以写成统一格式：
求和可以写成内积的形式，所以求和项可以直接表示为WF。看到这个是不是很熟悉？最大熵模型。
模型确定后，就剩下学习了~~
3 学习算法（参数估计）
3.1 改进的迭代尺度法
待续...
3.2 拟牛顿法
待续...
3.3 预测算法（维特比法）
待续...