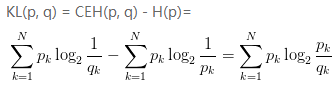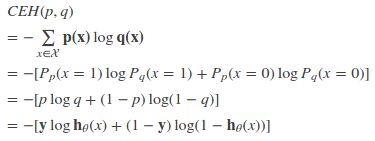线性回归、岭回归、逻辑回归、信息量与熵、多类的分类问题softmax、链式法则与BP神经网络

线性回归

       线性回归是我们比较熟悉的一类回归模型。已知自变量x和因变量y，利用这些值我们可以建立两者之间的线性关系。通常采用最小二乘法来求解。推导过程如下图：

岭回归

       当线性回归模型中存在多个相关变量时，它们的系数确定性变差并呈现高方差。比如说，在一个变量上的一个很大的正系数可能被在其相关变量上的类似大小的负系数抵消，岭回归就是通过在系数上施加约束来避免这种现象的发生。岭回归是一种求解近似解的方法，它的原理是牺牲解的无偏性来获得稳定的数值解。

       通常，引入一个正则参数来建立模型J。岭回归的解仍然是y的线性函数。

        注意到，岭回归在不同自变量的不同度量下的解是不同的，因此在进行岭回归的时候，要先将X和Y标准化。

逻辑回归

       与多重线性回归实际上有很多相同之处，最大的区别就在于它们的因变量不同，其他的基本都差不多。逻辑回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释。所以实际中最常用的就是二分类。逻辑回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别），所以利用了Logistic函数（或称为Sigmoid函数），它将数据拟合到logistic函数中，从而能够完成对事件发生的概率进行预测。

       主要用途：1、寻找危险因素：寻找某一疾病的危险因素等；2、预测：根据模型，预测在不同的自变量情况下，发生某病或某种情况的概率有多大；3、判别：实际上跟预测有些类似，也是根据模型，判断某人属于某病或属于某种情况的概率有多大，也就是看一下这个人有多大的可能性是属于某病。

       主要步骤是：1、寻找预测函数h函数（即hypothesis）；2、构造J函数（损失函数）；3、想办法使得J函数最小并求得回归参数（θ）

       

由图片可知，已经将log取为ln。

向量化及正则化见链接http://blog.csdn.net/pakko/article/details/37878837

************************************************************************************分界线******************************************************************************************

信息量

       信息量的大小应该可以衡量事件发生的“惊讶程度”或不确定性：如果有人告诉我们有个相当不可能的事件发生了，我们收到的信息要多于我们被告知某个很可能发生的事件发生时收到的信息。如果我们知道某件事情一定会发生，那么我们就不会接收到信息。 也就是说，信息量应该连续依赖于事件发生的概率分布p(x) 。因此，我们想要寻找一个基于概率p(x)计算信息量的函数h(x)，它应该具有如下性质：
       1、h(x) >= 0，因为信息量表示得到多少信息，不应该为负数。
       2、h(x, y) = h(x) + h(y)，也就是说，对于两个不相关事件x和y，我们观察到两个事件x, y同时发生时获得的信息应该等于观察到事件各自发生时获得的信息之和；
       3、h(x)是关于p(x)的单调递减函数，也就是说，事件x越容易发生（概率p(x)越大），信息量h(x)越小。
       又因为如果两个不相关事件是统计独立的，则有p(x, y) = p(x)p(y)。根据不相关事件概率可乘、信息量可加，很容易想到对数函数，看出h(x)一定与p(x)的对数有关。因此，有信息的量化计算：

                                                                                                               

熵（信息熵）

       对于一个随机变量X而言，它的所有可能取值的信息量的期望就称为熵。熵的本质的另一种解释：最短平均编码长度（对于离散变量）。
       离散变量：

                                                         

       连续变量：

                                                                                                           

交叉熵

       现有关于样本集的2个概率分布p和q，其中p为真实分布，q非真实分布。按照真实分布p来衡量识别一个样本的熵，即基于分布p给样本进行编码的最短平均编码长度为：

                                                                                               

       如果使用非真实分布q来给样本进行编码，则是基于分布q的信息量的期望（最短平均编码长度），由于用q来编码的样本来自分布p，所以期望与真实分布一致。所以基于分布q的最短平均编码长度，也即交叉熵的定义为：

                                                                                        

相对熵

       将由q得到的平均编码长度比由p得到的平均编码长度多出的bit数，即使用非真实分布q计算出的样本的熵(交叉熵)，与使用真实分布p计算出的样本的熵的差值，称为相对熵，又称KL散度。

                                                   

       相对熵（KL散度）用于衡量两个概率分布p和q的差异。注意，KL(p, q)意味着将分布p作为真实分布，q作为非真实分布，因此KL(p, q) != KL(q, p)。

代价函数与交叉熵

       若p(x) 是数据的真实概率分布，q(x) 是由数据计算得到的概率分布。机器学习的目的就是希望q(x)尽可能地逼近甚至等于p(x) ，从而使得相对熵接近最小值0。由于真实的概率分布是固定的，相对熵公式的后半部分（-H(p)） 就成了一个常数。那么相对熵达到最小值的时候，也意味着交叉熵达到了最小值。对q(x) 的优化就等效于求交叉熵的最小值。另外，对交叉熵求最小值，也等效于求最大似然估计（maximum likelihood estimation）。

       特别地，在逻辑回归中，p:真实样本分布，服从参数为p的0-1分布，即X~B(1,p)，P(X=1)=y,P(X=0)=1-y；

                                               q:待估计的模型，服从参数为q的0-1分布，即X~B(1,q)，P(X=1)=h(x),P(X=0)=1-h(x)

其中，h(x)为逻辑回归中的预测函数。

       两者的交叉熵为：

                                                         

对所有训练样本取均值得：

                                                         

这个结果与通过最大似然估计方法求出来的结果一致。

**************************************************************************************分界线******************************************************************************************

多类的分类问题softmax

       0-1分类问题解决将一个样本分配到A还是B的问题，总共只有两个类。而多类分类问题则包含多个类。

***************************************************************************************分界线**************************************************************************************

链式法则与BP神经网络

       最著名的运用bp算法的是训练神经网络，如果神经网络只有一个一层，通过梯度下降可以直接调整这一层的权重，但如果有多层，需要调整各个层次的权重，所以就需要链式求导法则求出各个层的梯度。

      参考链接 https://www.cnblogs.com/huahuahu/p/dao-shu-duo-yuan-han-shu-ti-du-lian-shi-fa-ze-ji-B.html

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

References

信息量、熵、交叉熵、相对熵与代价函数 https://www.cnblogs.com/llhthinker/p/7287029.html