数学建模三剑客MSN

1. 前言

不管是不是巴萨的球迷，只要你喜欢足球，就一定听说过梅西(Messi)、苏亚雷斯(Suarez)和内马尔(Neymar)这个MSN组合。在众多的数学建模辅助工具中，也有一个犀利无比的MSN组合，他们就是python麾下大名鼎鼎的 Matplotlib + Scipy + Numpy三剑客。

本文是我整理的MSN学习笔记，有些理解可能比较肤浅，甚至是错误的。如果因此误导了某位看官，在工作中造成重大失误或损失，我顶多只能赔偿一顿饭——还得是我们楼下的十元盒饭。特此声明。

文中代码均从我的这台时不时出点问题、闹个情绪的Yoga 3 pro上复制而来，这意味着所有的代码均可在下面的运行环境中顺利运行：

• pyhton 2.7.8
• numpy 1.11.1
• scipy 0.16.1
• matplotlib 1.5.1

---

2. 三剑客之Numpy

numpy是一个开源的python科学计算库，包含了很多实用的数学函数，涵盖线性代数、傅里叶变换和随机数生成等功能。最初的numpy其实是scipy的一部分，后来才从scipy中分离出来。

numpy不是python的标准库，需要单独安装。假定你的运行环境已经安装了python包管理工具pip，numpy的安装就非常简单：

pip install numpy

2.1 数组对象

ndarray是多维数组对象，也是numpy最核心的对象。在numpy中，数组的维度(dimensions)叫做轴(axes)，轴的个数叫做秩(rank)。通常，一个numpy数组的所有元素都是同一种类型的数据，而这些数据的存储和数组的形式无关。

下面的例子，创建了一个三维的数组（在导入numpy时，一般都简写成np）。

import numpy as np
a = np.array([[1,2,3],[4,5,6],[7,8,9]])

2.1.1 数据类型

numpy支持的数据类型主要有布尔型(bool)、整型(integrate)、浮点型(float)和复数型(complex)，每一种数据类型根据占用内存的字节数又分为多个不同的子类型。常见的数据类型见下表。

类型	描述
bool	用1位存储的布尔类型（值为TRUE或FALSE）
inti	由所在平台决定其精度的整数（一般为int32或int64）
int8	1字节整数
int16	2字节整数
int32	4字节整数
int64	8字节整数
uint8	1字节无符号整数
uint16	2字节无符号整数
uint32	4字节无符号整数
uint64	8字节无符号整数
float16	半精度浮点数（16位），1位符号，5位指数，10位尾数
float32	单精度浮点数（32位），1位符号，8位指数，23位尾数
float64/float	双精度浮点数（64位），1位符号，11位指数，52位尾数
complex64	复数，分别用32位表示实部和虚部
complex128/complex	复数，分别用64位表示实部和虚部

2.1.2 创建数组

通常，我们用np.array()创建数组。如果仅仅是创建一维数组，也可以使用np.arange()或者np.linspace()的方法。np.zeros()、np.ones()、np.eye()则可以构造特殊的数据。np.random.randint()和np.random.random()则可以构造随机数数组。

>>> np.array([[1,2,3],[4,5,6]])                # 默认元素类型为int32
array([[1, 2, 3],
       [4, 5, 6]])
>>> np.array([[1,2,3],[4,5,6]], dtype=np.int8) # 指定元素类型为int8
array([[1, 2, 3],
       [4, 5, 6]], dtype=int8)
>>> np.arange(5)                               # 默认元素类型为int32
array([0, 1, 2, 3, 4])
>>> np.arange(3,8, dtype=np.int8)              # 指定元素类型为int8
array([3, 4, 5, 6, 7], dtype=int8)
>>> np.arange(12).reshape(3,4)                 # 改变shape
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
>>> np.linspace(1,2,5)                        # 从1到2生成5个浮点数
array([ 1.  ,  1.25,  1.5 ,  1.75,  2.  ])
>>> np.zeros((2,3))                            # 全0数组
array([[ 0.,  0.,  0.],
       [ 0.,  0.,  0.]])
>>> np.ones((2,3))                             # 全1数组
array([[ 1.,  1.,  1.],
       [ 1.,  1.,  1.]])
>>> np.eye(3)                                  # 主对角线元素为1其他元素为0
array([[ 1.,  0.,  0.],
       [ 0.,  1.,  0.],
       [ 0.,  0.,  1.]])
>>> np.random.random((2,3))                    # 生成[0,1)之间的随机浮点数
array([[ 0.84731148,  0.8222318 ,  0.85799278],
       [ 0.59371558,  0.92330741,  0.04518351]])
>>> np.random.randint(0,10,(3,2))              # 生成[0,10)之间的随机整数
array([[2, 4],
       [8, 3],
       [8, 5]])

2.1.3 构造复杂数组

很多时候，我们需要从简单的数据结构，构造出复杂的数组。例如，用一维的数据生成二维格点。

2.1.3.1 重复数组: tile

>>> a = np.arange(5)
>>> a
array([0, 1, 2, 3, 4])
>>> np.tile(a, 2)
array([0, 1, 2, 3, 4, 0, 1, 2, 3, 4])
>>> np.tile(a, (3,2))
array([[0, 1, 2, 3, 4, 0, 1, 2, 3, 4],
       [0, 1, 2, 3, 4, 0, 1, 2, 3, 4],
       [0, 1, 2, 3, 4, 0, 1, 2, 3, 4]])

2.1.3.2 重复元素: repeat

>>> a = np.arange(5)
>>> a
array([0, 1, 2, 3, 4])
>>> a.repeat(2)
array([0, 0, 1, 1, 2, 2, 3, 3, 4, 4])

2.1.3.3 一维数组网格化: meshgrid

>>> a = np.arange(5)
>>> b = np.arange(5,10)
>>> np.meshgrid(a,b)
[array([[0, 1, 2, 3, 4],
       [0, 1, 2, 3, 4],
       [0, 1, 2, 3, 4],
       [0, 1, 2, 3, 4],
       [0, 1, 2, 3, 4]]), array([[5, 5, 5, 5, 5],
       [6, 6, 6, 6, 6],
       [7, 7, 7, 7, 7],
       [8, 8, 8, 8, 8],
       [9, 9, 9, 9, 9]])]
>>> 

2.1.3.4 指定范围和分割方式的网格化: mgrid

>>> np.mgrid[0:1:2j, 1:2:3j]
array([[[ 0. ,  0. ,  0. ],
        [ 1. ,  1. ,  1. ]],

       [[ 1. ,  1.5,  2. ],
        [ 1. ,  1.5,  2. ]]])
>>> np.mgrid[0:1:0.3, 1:2:0.4]
array([[[ 0. ,  0. ,  0. ],
        [ 0.3,  0.3,  0.3],
        [ 0.6,  0.6,  0.6],
        [ 0.9,  0.9,  0.9]],

       [[ 1. ,  1.4,  1.8],
        [ 1. ,  1.4,  1.8],
        [ 1. ,  1.4,  1.8],
        [ 1. ,  1.4,  1.8]]])

上面的例子中用到了虚数。构造虚数的方法如下：

>>> complex(2,5)
(2+5j)

2.1.4 数组的属性

numpy的数组对象除了一些常规的属性外，也有几个类似转置、扁平迭代器等看起来更像是方法的属性。扁平迭代器也许是遍历多维数组的一个简明方法，下面的代码给出了一个例子。

>>> a = np.array([[1,2,3],[4,5,6]])
>>> a.dtype               # 数组元素的数据类型
dtype('int32')
>>> a.dtype.itemsize      # 数组元素占据的内存字节数
4
>>> a.itemsize            # 数组元素占据的内存字节数
4
>>> a.shape               # 数组的维度
(2, 3)
>>> a.size                # 数组元素个数
6
>>> a.T                   # 数组行变列，类似于transpose()
array([[1, 4],
       [2, 5],
       [3, 6]])
>>> a.flat                # 返回一个扁平迭代器，用于遍历多维数组
<numpy.flatiter object at 0x037188F0>
>>> for item in a.flat:
	print item
1
2
... 

2.1.5 改变数组维度

numpy数组的存储顺序和数组的维度是不相干的，因此改变数组的维度是非常便捷的操作，除resize()外，这一类操作不会改变所操作的数组本身的存储顺序。

>>> a = np.array([[1,2,3],[4,5,6]])
>>> a.shape                     # 查看数组维度
(2, 3)
>>> a.reshape(3,2)              # 返回3行2列的数组
array([[1, 2],
       [3, 4],
       [5, 6]])
>>> a.ravel()                   # 返回一维数组
array([1, 2, 3, 4, 5, 6])
>>> a.transpose()               # 行变列（类似于矩阵转置）
array([[1, 4],
       [2, 5],
       [3, 6]])
>>> a.resize((3,2))             # 类似于reshape，但会改变所操作的数组
>>> a
array([[1, 2],
       [3, 4],
       [5, 6]])

2.1.6 索引和切片

对于一维数组的索引和切片，numpy和python的list一样，甚至更灵活。

a = np.arange(9)
>>> a[-1]                            # 最后一个元素
8
>>> a[2:5]                           # 返回第2到第5个元素
array([2, 3, 4])
>>> a[:7:3]                          # 返回第0到第7个元素，步长为3
array([0, 3, 6])
>>> a[::-1]                          # 返回逆序的数组
array([8, 7, 6, 5, 4, 3, 2, 1, 0])

假设有一栋2层楼，每层楼内的房间都是3排4列，那我们可以用一个三维数组来保存每个房间的居住人数（当然，也可以是房间面积等其他数值信息）。

>>> a = np.arange(24).reshape(2,3,4)    # 2层3排4列
>>> a
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],

       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]]])
>>> a[1][2][3]                          # 虽然可以这样
23
>>> a[1,2,3]                            # 但这才是规范的用法
23
>>> a[:,0,0]                            # 所有楼层的第1排第1列
array([ 0, 12])
>>> a[0,:,:]                            # 1楼的所有房间，等价与a[0]或a[0,...]
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
>>> a[:,:,1:3]                          # 所有楼层所有排的第2到4列
array([[[ 1,  2],
        [ 5,  6],
        [ 9, 10]],

       [[13, 14],
        [17, 18],
        [21, 22]]])
>>> a[1,:,-1]                           # 2层每一排的最后一个房间
array([15, 19, 23])

2.1.7 数组合并

数组合并除了下面介绍的水平合并、垂直合并、深度合并外，还有行合并、列合并，以及concatenate()等方式。假如你比我还懒，那就只了解前三种方法吧，足够用了。

>>> a = np.arange(9).reshape(3,3)
>>> b = np.arange(9,18).reshape(3,3)
>>> a
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])
>>> b
array([[ 9, 10, 11],
       [12, 13, 14],
       [15, 16, 17]])
>>> np.hstack((a,b))                        # 水平合并
array([[ 0,  1,  2,  9, 10, 11],
       [ 3,  4,  5, 12, 13, 14],
       [ 6,  7,  8, 15, 16, 17]])
>>> np.vstack((a,b))                        # 垂直合并
array([[ 0,  1,  2],
       [ 3,  4,  5],
       [ 6,  7,  8],
       [ 9, 10, 11],
       [12, 13, 14],
       [15, 16, 17]])
>>> np.dstack((a,b))                        # 深度合并
array([[[ 0,  9],
        [ 1, 10],
        [ 2, 11]],

       [[ 3, 12],
        [ 4, 13],
        [ 5, 14]],

       [[ 6, 15],
        [ 7, 16],
        [ 8, 17]]])

2.1.8 数组拆分

拆分是合并的逆过程，概念是一样的，但稍微有一点不同：

>>> a = np.arange(9).reshape(3,3)
>>> np.hsplit(a, 3)                        # 水平拆分，返回list
[array([[0],
       [3],
       [6]]), array([[1],
       [4],
       [7]]), array([[2],
       [5],
       [8]])]
>>> np.vsplit(a, 3)                        # 垂直拆分，返回list
[array([[0, 1, 2]]), array([[3, 4, 5]]), array([[6, 7, 8]])]
>>> a = np.arange(27).reshape(3,3,3)
>>> np.dsplit(a, 3)                        # 深度拆分，返回list
[array([[[ 0],
        [ 3],
        [ 6]],

       [[ 9],
        [12],
        [15]],

       [[18],
        [21],
        [24]]]), array([[[ 1],
        [ 4],
        [ 7]],

       [[10],
        [13],
        [16]],

       [[19],
        [22],
        [25]]]), array([[[ 2],
        [ 5],
        [ 8]],

       [[11],
        [14],
        [17]],

       [[20],
        [23],
        [26]]])]

2.1.9 数组运算

数组和常数的四则运算，是数组的每一个元素分别和常数运算；数组和数组的四则运算则是两个数组对应元素的运算（两个数组有相同的shape，否则抛出异常）。

>>> a = np.arange(4, dtype=np.float32).reshape(2,2)
>>> b = np.arange(4, 8, dtype=np.float32).reshape(2,2)
>>> a+2                # 数组和常数可以进行四则运算
array([[ 2.,  3.],
       [ 4.,  5.]], dtype=float32)
>>> a/b                # 数组和数组可以进行四则运算
array([[ 0.        ,  0.2       ],
       [ 0.33333334,  0.42857143]], dtype=float32) 
>>> a == b             # 最神奇的是，数组可以判断对应元素是否相等
array([[False, False],
       [False, False]], dtype=bool)
>>> (a == b).all()     # 判断数组是否相等
False

特别提示：如果想对数组内符合特定条件的元素做特殊处理，下面的代码也许有用。

>>> a = np.arange(6).reshape((2,3))
>>> a
array([[0, 1, 2],
       [3, 4, 5]])
>>> (a>2)&(a<=4)
array([[False, False, False],
       [ True,  True, False]], dtype=bool)
>>> a[(a>2)&(a<=4)]
array([3, 4])
>>> a[(a>2)&((a<=4))] += 10
>>> a
array([[ 0,  1,  2],
       [13, 14,  5]])

2.1.10 数组方法和常用函数

数组对象本身提供了计算算数平均值、求最大最小值等内置方法，numpy也提供了很多实用的函数。为了缩减篇幅，下面的代码仅以一维数组为例，展示了这些方法和函数用法。事实上，大多数情况下这些方法和函数对于多维数组同样有效，只有少数例外，比如compress函数。

>>> a = np.array([3,2,4])
>>> a.sum()                   # 所有元素的和
9
>>> a.prod()                  # 所有元素的乘积
24
>>> a.mean()                  # 所有元素的算数平均值
3.0
>>> a.max()                   # 所有元素的最大值
4
>>> a.min()                   # 所有元素的最小值
2
>>> a.clip(3,4)               # 小于3的元素替换为3，大于4的元素替换为4
array([3, 3, 4])
>>> a.compress(a>2)           # 返回大于2的元素组成的数组
array([3, 4])
>>> a.tolist()                # 返回python的list
[3, 2, 4]
>>> a.var()                   # 计算方差（元素与均值之差的平方的均值）
0.66666666666666663
>>> a.std()                   # 计算标准差（方差的算术平方根）
0.81649658092772603
>>> a.ptp()                   # 返回数组的最大值和最小值之差
2
>>> a.argmin()                # 返回最小值在扁平数组中的索引
1
>>> a.argmax()                # 返回最大值在扁平数组中的索引
2
>>> np.where(a == 2)          # 返回所有值为2的元素的索引
(array([1]),)
>>> np.diff(a)                # 返回相邻元素的差
array([-1,  2])
>>> np.log(a)                 # 返回对数数组
array([ 1.09861229,  0.69314718,  1.38629436])
>>> np.exp(a)                 # 返回指数数组
array([ 20.08553692,   7.3890561 ,  54.59815003])
>>> np.sqrt(a)                # 返回开方数组
array([ 1.73205081,  1.41421356,  2.        ])
>>> np.msort(a)               # 数组排序
array([2, 3, 4])
>>> a = np.array([1,4,7])
>>> b = np.array([8,5,2])
>>> np.maximum(a, b)          # 返回多个数组中对应位置元素的最大值数组
array([8, 5, 7])
>>> np.minimum(a, b)          # 返回多个数组中对应位置元素的最小值数组
array([1, 4, 2])
>>> np.true_divide(a, b)      # 对整数实现真正的数学除法运算
array([ 0.125,  0.8  ,  3.5  ])

2.2 矩阵对象

matrix是矩阵对象，继承自ndarray类型，因此含有ndarray的所有数据属性和方法。不过，当你把矩阵对象当数组操作时，需要注意以下几点：

• matrix对象总是二维的，即使是展平（ravel函数）操作或是成员选择，返回值也是二维的
• matrix对象和ndarray对象混合的运算总是返回matrix对象

2.2.1 创建矩阵

matrix对象可以使用一个Matlab风格的字符串来创建（以空格分隔列，以分号分隔行的字符串），也可以用数组来创建。

>>> np.mat('1 4 7; 2 5 8; 3 6 9')
matrix([[1, 4, 7],
        [2, 5, 8],
        [3, 6, 9]])
>>> np.mat(np.arange(1,10).reshape(3,3))
matrix([[1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]])

2.2.2 矩阵的特有属性

矩阵有几个特有的属性使得计算更加容易，这些属性有：

>>> m = np.mat(np.arange(1,10).reshape(3,3))
>>> m
matrix([[1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]])
>>> m.T             # 返回自身的转置
matrix([[1, 4, 7],
        [2, 5, 8],
        [3, 6, 9]])
>>> m.H             # 返回自身的共轭转置
matrix([[1, 4, 7],
        [2, 5, 8],
        [3, 6, 9]])
>>> m.I             # 返回自身的逆矩阵
matrix([[ -4.50359963e+15,   9.00719925e+15,  -4.50359963e+15],
        [  9.00719925e+15,  -1.80143985e+16,   9.00719925e+15],
        [ -4.50359963e+15,   9.00719925e+15,  -4.50359963e+15]])
>>> m.A             # 返回自身数据的二维数组的一个视图
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

2.2.3 矩阵乘法

对ndarray对象而言，星号是按元素相乘，dot()函数则当作矩阵相乘。对于matrix对象来说，星号和dot()函数都是矩阵相乘。特别的，对于一维数组，dot()函数实现的是向量点乘（结果是标量），但星号实现的却不是差乘。

>>> a = np.array([1,2,3])
>>> b = np.array([4,5,6])
>>> a*b               # 一维数组，元素相乘
array([ 4, 10, 18])
>>> np.dot(a,b)       # 一维数组，元素相乘再求和
32
>>> a = np.array([[1,2],[3,4]])
>>> b = np.array([[5,6],[7,8]])
>>> a*b               # 多维数组，元素相乘
array([[ 5, 12],
       [21, 32]])
>>> np.dot(a,b)       # 多维数组，实现的是矩阵相乘
array([[19, 22],
       [43, 50]])
>>> m = np.mat(a)
>>> n = np.mat(b)
>>> np.dot(m,n)       # 矩阵相乘
matrix([[19, 22],
        [43, 50]])
>>> m*n               # 矩阵相乘
matrix([[19, 22],
        [43, 50]])

2.3 线性代数模块

numpy.linalg 是numpy的线性代数模块，可以用来解决逆矩阵、特征值、线性方程组以及行列式等问题。

2.3.1 计算逆矩阵

尽管matrix对象本身有逆矩阵的属性，但用numpy.linalg模块求解矩阵的逆，也是非常简单的。

m = np.mat('0 1 2; 1 0 3; 4 -3 8')
mi = np.linalg.inv(m)           # mi即为m的逆矩阵。何以证明？
m * mi                          # 矩阵与其逆矩阵相乘，结果为单位矩阵
matrix([[ 1.,  0.,  0.],
        [ 0.,  1.,  0.],
        [ 0.,  0.,  1.]])

2.3.2 计算行列式

如何计算行列式，我早已经不记得了，但手工计算行列式的痛苦，我依然记忆犹新。现在好了，你在手机上都可以用numpy轻松搞定（前提是你的手机上安装了python + numpy）。

m = np.mat('0 1 2; 1 0 3; 4 -3 8')
np.linalg.det(m)                # 什么？这就成了？
2.0

2.3.3 计算特征值和特征向量

截至目前，我的工作和特征值、特征向量还有没任何关联。记录这一节，纯粹是为了我女儿，她正在读数学专业。

m = np.mat('0 1 2; 1 0 3; 4 -3 8')
>>> np.linalg.eigvals(m)        # 计算特征值
array([ 7.96850246, -0.48548592,  0.51698346])
>>> np.linalg.eig(m)            # 返回特征值及其对应特征向量的元组
(array([ 7.96850246, -0.48548592,  0.51698346]), matrix([[ 0.26955165,  0.90772191, -0.74373492],
        [ 0.36874217,  0.24316331, -0.65468206],
        [ 0.88959042, -0.34192476,  0.13509171]]))

2.3.4 求解线性方程组

有线性方程组如下：

x - 2y + z = 0
2y -8z = 8
-4x + 5y + 9z = -9

求解过程如下：

>>> A = np.mat('1 -2 1; 0 2 -8; -4 5 9')
>>> b = np.array([0, 8, -9])
>>> np.linalg.solve(A, b)
array([ 29.,  16.,   3.])  # x = 29, y = 16, z = 3

3. 三剑客之Matplotlib

matplotlib 是python最著名的绘图库，它提供了一整套和Matlab相似的命令API，十分适合交互式地进行制图。而且也可以方便地将它作为绘图控件，嵌入GUI应用程序中。matplotlib 可以绘制多种形式的图形包括普通的线图，直方图，饼图，散点图以及误差线图等；可以比较方便的定制图形的各种属性比如图线的类型，颜色，粗细，字体的大小等；它能够很好地支持一部分 TeX 排版命令，可以比较美观地显示图形中的数学公式。

3.1 pylot介绍

Matplotlib 包含了几十个不同的模块， 如 matlab、mathtext、finance、dates 等，而 pylot 则是我们最常用的绘图模块，这也是本文介绍的重点。

3.1.1 中文显示问题的解决方案

有很多方法可以解决此问题，但下面的方法恐怕是最简单的解决方案了（我只在windows平台上测试过，其他平台请看官自测）。如果想了解更多，也可以参考我N年前的一片博文：matplotlib显示中文的解决方案

>>> import matplotlib.pyplot as plt
>>> plt.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
>>> plt.rcParams['axes.unicode_minus'] = False     # 解决保存图像时'-'显示为方块的问题

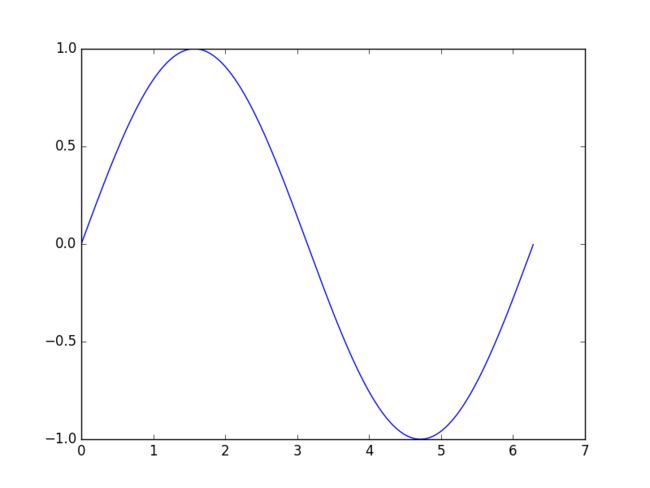
3.1.2 绘制最简单的图形

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> x = np.arange(0, 2*np.pi, 0.01)
>>> y = np.sin(x)
>>> plt.plot(x, y)
>>> plt.show()

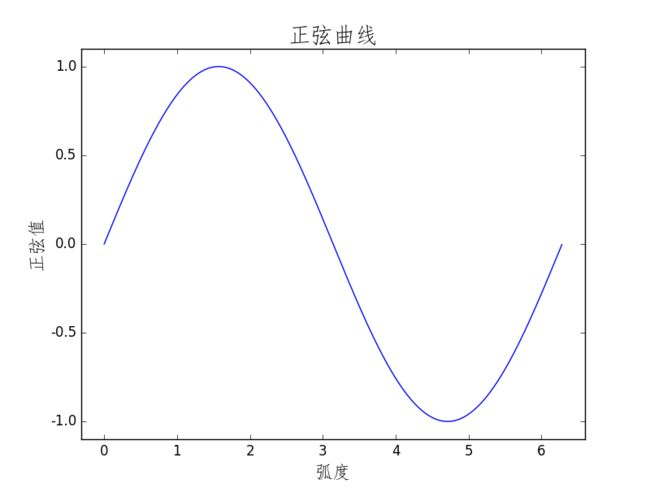
3.1.3 设置标题、坐标轴名称、坐标轴范围

如果你在python的shell中运行下面的代码，而shell的默认编码又不是utf-8的话，中文可能仍然会显示为乱码。你可以尝试着把 u’正弦曲线’ 写成 ‘正弦曲线’.decode(‘gbk’)或者’正弦曲线’.decode(‘utf-8’)

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from pylab import mpl
>>> mpl.rcParams['font.sans-serif'] = ['FangSong']
>>> mpl.rcParams['axes.unicode_minus'] = False
>>> x = np.arange(0, 2*np.pi, 0.01)
>>> y = np.sin(x)
>>> plt.plot(x, y)
>>> plt.title(u'正弦曲线', fontdict={'size':20})      # 设置标题
>>> plt.xlabel(u'弧度', fontdict={'size':16})         # 显示横轴名称
>>> plt.ylabel(u'正弦值', fontdict={'size':16})       # 显示纵轴名称
>>> plt.axis([-0.1*np.pi, 2.1*np.pi, -1.1, 1.1])     # 设置坐标轴范围
>>> plt.axis('equal')                                # xy轴等比例保持
>>> plt.show()

3.1.4 设置点和线的样式、宽度、颜色

plt.plot函数的调用形式如下：

plot(x, y, color='green', linestyle='dashed', linewidth=1, marker='o', markerfacecolor='blue', markersize=6)
plot(x, y, c='g', ls='--', lw=1, marker='o', mfc='blue', ms=6)

1. color指定线的颜色，可简写为“c”。颜色的选项为：

• 蓝色： ‘b’ (blue)
• 绿色： ‘g’ (green)
• 红色： ‘r’ (red)
• 墨绿： ‘c’ (cyan)
• 洋红： ‘m’ (magenta)
• 黄色： ‘y’ (yellow)
• 黑色： ‘k’ (black)
• 白色： ‘w’ (white)
• 灰度表示： e.g. 0.75 ([0,1]内任意浮点数)
• RGB表示法： e.g. ‘#2F4F4F’ 或 (0.18, 0.31, 0.31)

1. linestyle指定线型，可简写为“ls”。线型的选项为：

• 实线： ‘-’ (solid line)
• 虚线： ‘–’ (dashed line)
• 虚点线： ‘-.’ (dash-dot line)
• 点线： ‘:’ (dotted line)
• 无： '‘或’ ‘或’None’

1. linewidth指定线宽，可简写为“lw”。

2. marker描述数据点的形状

• 点线： ‘.’
• 点线： ‘o’
• 加号： '+
• 叉号： ‘x’
• 上三角： ‘^’
• 上三角： ‘v’

1. markerfacecolor指定数据点标记的表面颜色，可 简写为“ mfc”。

2. markersize指定数据点标记的大小，可 简写为“ ms”。

3.1.5 文本标注和图例

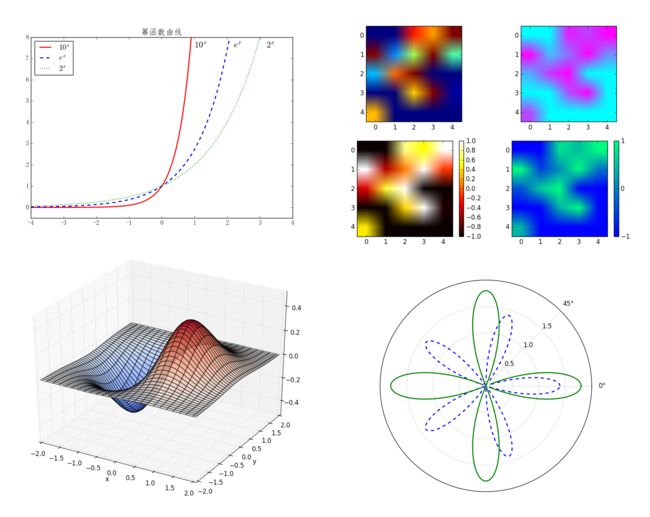
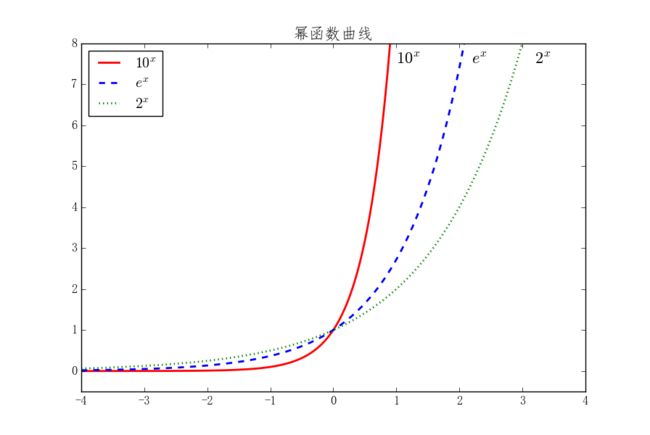
我们分别使用不同的线型、颜色来绘制以10、e、2为基的一组幂函数曲线，演示文本标注和图例的使用。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from pylab import mpl
>>> mpl.rcParams['font.sans-serif'] = ['FangSong']
>>> mpl.rcParams['axes.unicode_minus'] = False
>>> x = np.linspace(-4, 4, 200)
>>> f1 = np.power(10, x)
>>> f2 = np.power(np.e, x)
>>> f3 = np.power(2, x)
>>> plt.plot(x, f1, 'r', ls='-', linewidth=2, label='$10^x$')
>>> plt.plot(x, f2, 'b', ls='--', linewidth=2, label='$e^x$')
>>> plt.plot(x, f3, 'g', ls=':', linewidth=2, label='$2^x$')
>>> plt.axis([-4, 4, -0.5, 8])
>>> plt.text(1, 7.5, r'$10^x$', fontsize=16)
>>> plt.text(2.2, 7.5, r'$e^x$', fontsize=16)
>>> plt.text(3.2, 7.5, r'$2^x$', fontsize=16)
>>> plt.title('幂函数曲线', fontsize=16)
>>> plt.legend(loc='upper left')
>>> plt.show()

在绘制图例时，loc用于指定图例的位置，可用的选项有：

• best
• upper right
• upper left
• lower left
• lower right

3.2 绘制多轴图

在介绍如何将多幅子图绘制在同一画板的同时，顺便演示如何绘制直线和矩形。我们可以使用subplot函数快速绘制有多个轴的图表。subplot函数的调用形式如下：

subplot(numRows, numCols, plotNum)

subplot将整个绘图区域等分为numRows行 * numCols列个子区域，然后按照从左到右，从上到下的顺序对每个子区域进行编号，左上的子区域的编号为1。如果numRows，numCols和plotNum这三个数都小于10的话，可以把它们缩写为一个整数，例如subplot(323)和subplot(3,2,3)是相同的。subplot在plotNum指定的区域中创建一个轴对象。如果新创建的轴和之前创建的轴重叠的话，之前的轴将被删除。

>>> import matplotlib.pyplot as plt
>>> plt.subplot(221) # 两行两列的第1个位置
>>> plt.axis([-1, 2, -1, 2])
>>> plt.axhline(y=0.5, color='b')
>>> plt.axhline(y=0.5, xmin=0.25, xmax=0.75, color='r')
>>> plt.subplot(222) # 两行两列的第2个位置
>>> plt.axis([-1, 2, -1, 2])
>>> plt.axvline(x=0, ymin=0, linewidth=4, color='r')
>>> plt.axvline(x=1.0, ymin=-0.5, ymax=0.5, linewidth=4, color='g')
>>> plt.subplot(212) # 两行一列的第2个位置
>>> plt.axis([-1, 2, -1, 2])
>>> plt.axvspan(1.25, 1.55, facecolor='g', alpha=0.5)
>>> plt.axhspan(0.25, 0.75, facecolor='0.5', alpha=0.5)
>>> plt.show()

3.3 常用绘图类型

3.3.1 直方图

用numpy随机生成一个符合正态分布的数据集，统计分段区域内数据的个数。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> data = np.random.normal(5.0, 3.0, 1000)
>>> plt.hist(data)
>>> bins = np.arange(-5, 16, 1)
>>> plt.hist(data, bins) # 使用自定义的分段区域
>>> plt.show()

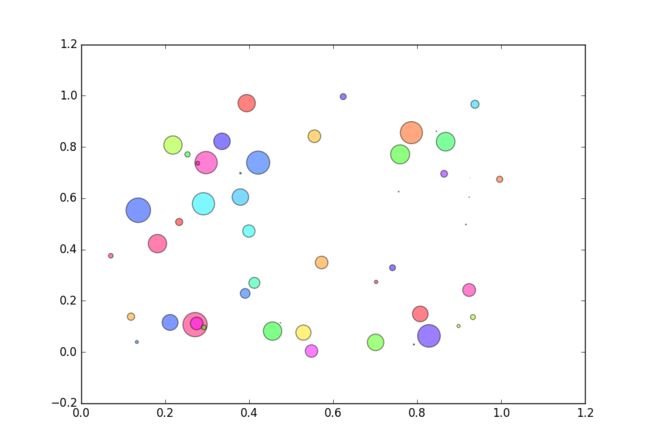
3.3.2 散点图

使用plot()绘图时，如果指定样式参数为仅绘制数据点（linestyle=‘None’），那么所绘制的就是一幅散列图。这种方法所绘制的点无法单独指定数据点的颜色和大小，而使用scatter()绘制散列图就可以指定每个点的颜色和大小。

plt.scatter函数的调用形式如下：

scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None, vmin=None, vmax=None, alpha=None, linewidths=None, verts=None, edgecolors=None, hold=None, data=None, **kwargs)

scatter()的前两个参数是数组，分别指定每个点的X轴和Y轴的坐标。s参数指定点的大 小，值和点的面积成正比，它可以是一个数，指定所有点的大小，也可以是数组，分别对每个点指定大小。c参数指定每个点的颜色，可以是数值或数组。这里使用一维数组为每个点指定了一个数值。通过颜色映射表，每个数值都会与一个颜色相对应。默认的颜色映射表中蓝色与最小值对应，红色与最大值对应。当c参数是形状为(N,3)或(N,4)的二维数组时，则直接表示每个点的RGB颜色。marker参数设置点的形状，可以是个表示形状的字符串，也可以是表示多边形的两个元素的元组，第一个元素表示多边形的边数，第二个元素表示多边形的样式，取值范围为0、1、2、3。0表示多边形，1表示星形，2表示放射形，3表示忽略边数而显示为圆形。alpha参数设置点的透明度。facecolors参数为“none”时，表示散列点没有填充色。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> x = np.random.rand(50)
>>> y = np.random.rand(50)
>>> area = np.pi * (15 * np.random.rand(50))**2
>>> color = 2 * np.pi * np.random.rand(50)
>>> plt.scatter(x, y, s=area, c=color, alpha=0.5, cmap=plt.cm.hsv)
>>> plt.show()

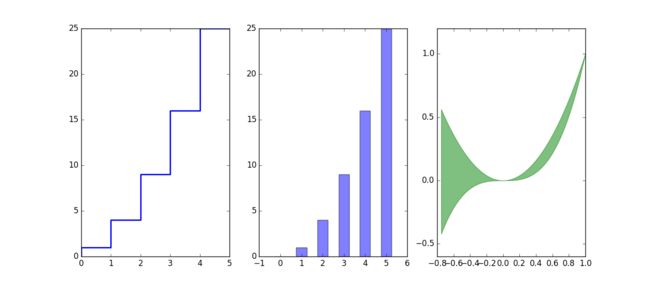
3.3.3 梯形图、柱状图、填充图

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> n = np.array([0,1,2,3,4,5])
>>> x = np.linspace(-0.75, 1., 100)
>>> plt.subplot(131)
>>> plt.step(n, n**2, lw=2)
>>> plt.subplot(132)
>>> plt.bar(n, n**2, align="center", width=0.5, alpha=0.5)
>>> plt.subplot(133)
>>> plt.fill_between(x, x**2, x**3, color="green", alpha=0.5)
>>> plt.show()

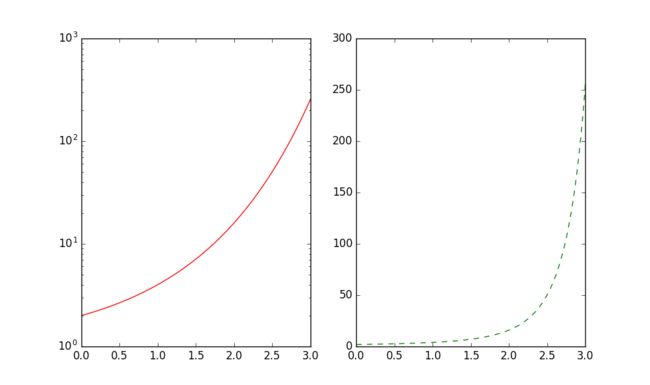
3.3.4 对数坐标

plot()所绘制图表的X-Y轴坐标都是算术坐标。绘制对数坐标图的函数有三个：semilogx()、semilogy()和loglog(),它们分别绘制X轴为对数坐标、Y轴为对数坐标以及两个轴都为对数坐标时的图表。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> x = np.linspace(0, 3, 100)
>>> y = np.power(2, np.power(2,x))
>>> plt.subplot(121)
>>> plt.semilogy(x, y , '-r')
>>> plt.subplot(122)
>>> plt.plot(x,y, '--g')
>>> plt.show()

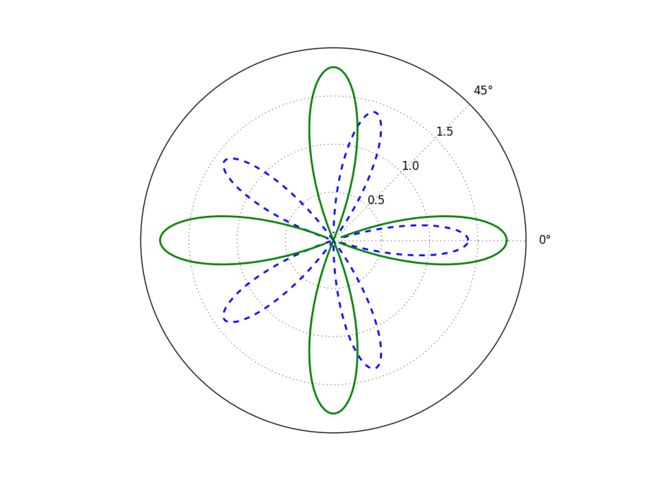
3.3.5极坐标绘图

极坐标系是和笛卡尔(X-Y)坐标系完全不同的坐标系，极坐标系中的点由一个夹角和一段相对中心点的距离来表示。polar(theta, r, **kwargs)可以直接创建极坐标子图并在其中绘制曲线。也可以使用程序中调用subplot()创建子图时通过设 polar参数为True,创建一个极坐标子图，然后调用plot()在极坐标子图中绘图。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> theta = np.arange(0, 2*np.pi, 0.02)
>>> plt.polar(theta, 1.4*np.cos(5*theta), "--", linewidth=2)
>>> plt.polar(theta, 1.8*np.cos(4*theta), linewidth=2)
>>> plt.rgrids(np.arange(0.5, 2, 0.5), angle=45)
>>> plt.thetagrids([0, 45])thetagridlabel objects>)
>>> plt.show()
>>> 

3.4 2D绘图

3.4.1 等值线图

所谓等值线，是指由函数值相等的各点连成的平滑曲线。等值线可以直观地表示二元函数值的变化趋势，例如等值线密集的地方表示函数值在此处的变化较大。matplotlib中可以使用contour()和contourf()描绘等值线，它们的区别是：contourf()所得到的是带填充效果的等值线。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> y, x = np.ogrid[-2:2:200j, -3:3:300j]
>>> z = x * np.exp( - x**2 - y**2)
>>> extent = [np.min(x), np.max(x), np.min(y), np.max(y)]
>>> plt.subplot(121)
>>> cs = plt.contour(z, 10, extent=extent)
>>> plt.clabel(cs)
<a list of 8 text.Text objects>
>>> plt.subplot(122)
>>> plt.contourf(x.reshape(-1), y.reshape(-1), z, 20)
>>> plt.show()

为了更淸楚地区分X轴和Y轴，这里让它们的取值范围和等分次数均不相同.这样得 到的数组z的形状为(200, 300),它的第0轴对应Y轴、第1轴对应X轴。

调用contour()绘制数组z的等值线图，第二个参数为10,表示将整个函数的取值范围等分为10个区间,即显示的等值线图中将有9条等值线。可以使用extent参数指定等值线图的X轴和Y轴的数据范围。

contour()所返回的是一个QuadContourSet对象， 将它传递给clabel()，为其中的等值线标上对应的值。

调用contourf(),绘制将取值范围等分为20份、带填充效果的等值线图。这里演示了另外一种设置X、Y轴取值范围的方法，它的前两个参数分别是计算数组z时所使用的X轴和Y轴上的取样点,这两个数组必须是一维的。

3.4.2 二维数据的平面色彩显示

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> data=np.clip(np.random.randn(5,5),-1,1)
>>> plt.subplot(221)
>>> plt.imshow(data)
>>> plt.subplot(222)
>>> plt.imshow(data,cmap=plt.cm.cool)
>>> plt.subplot(223)
>>> plt.imshow(data,cmap=plt.cm.hot)
>>> plt.colorbar()
>>> plt.subplot(224)
>>> im = plt.imshow(data,cmap=plt.cm.winter)
>>> plt.colorbar(im, cmap=plt.cm.winter, ticks=[-1,0,1])
>>> plt.show()

3.5 3D绘图

虽然matplotlib主要专注于绘图，并且主要是二维的图形，但是它也有一些不同的扩展，能让我们在地理图上绘图，让我们把Excel和3D图表结合起来。在matplotlib的世界里，这些扩展叫做工具包（toolkits）。工具包是一些关注在某个话题（如3D绘图）的特定函数的集合。

比较流行的工具包有Basemap、GTK 工具、Excel工具、Natgrid、AxesGrid和mplot3d。

mpl_toolkits.mplot3工具包提供了一些基本的3D绘图功能，其支持的图表类型包括散点图（scatter）、曲面图（surf）、线图（line）和网格图（mesh）。虽然mplot3d不是一个最好的3D图形绘制库，但是它是伴随着matplotlib产生的，因此我们对其接口已经很熟悉了。

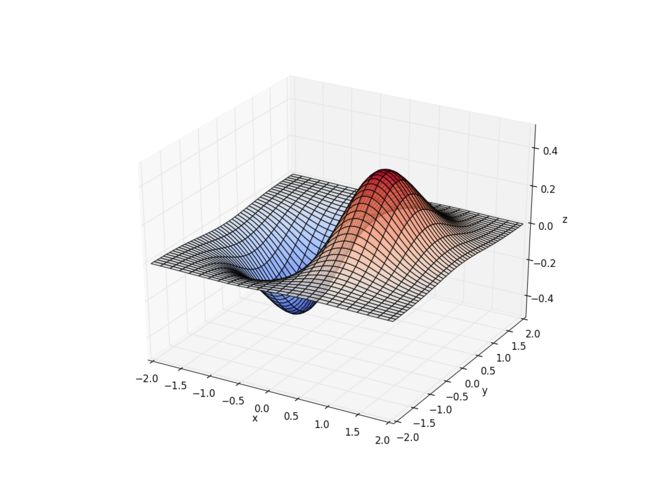
下面是一个使用plot_surface绘制3d曲面图的例子。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import mpl_toolkits.mplot3d
>>> x, y = np.mgrid[-2:2:50j,-2:2:50j]
>>> z = x*np.exp(-x**2-y**2)
>>> ax = plt.subplot(111,projection='3d')
>>> ax.plot_surface(x,y,z,rstride=2,cstride=1,cmap=plt.cm.coolwarm,alpha=0.8)
>>> ax.set_xlabel('x')
>>> ax.set_ylabel('y')
>>> ax.set_zlabel('z')
>>> plt.show()

4. 三剑客之Scipy

前面已经说过，最初的numpy其实是scipy的一部分，后来才从scipy中分离出来。scipy函数库在numpy库的基础上增加了众多的数学、科学以及工程计算中常用的库函数。例如线性代数、常微分方程数值求解、信号处理、图像处理、稀疏矩阵等等。由于其涉及的领域众多，我之于scipy，就像盲人摸大象，只能是摸到哪儿算哪儿。

4.1 插值

数据插值是数据处理过程中经常用到的技术，常用的插值有一维插值、二维插值、高阶插值等，常见的算法有线性插值、B样条插值、临近插值等。

4.1.1 一维插值

一维插值最常用的算法是线型插值和三阶样条插值，此外还有前点插值、后点插值、临近点插值、零阶插值（等同于前点插值）、一阶插值（等同于线性插值）、五阶插值等。下面的例子对以上8中插值方法进行了比较。

import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['FangSong']
plt.rcParams['axes.unicode_minus'] = False

x = np.linspace(0,10,11)
y = np.exp(-x/3.0)
x_new = np.linspace(0,10,100) # 期望在0-10之间变成100个数据点

f1 = interpolate.interp1d(x, y, kind='linear')
f2 = interpolate.interp1d(x, y, kind='nearest')
f3 = interpolate.interp1d(x, y, kind='zero')
f4 = interpolate.interp1d(x, y, kind='slinear')
f5 = interpolate.interp1d(x, y, kind='cubic')
f6 = interpolate.interp1d(x, y, kind='quadratic')
f7 = interpolate.interp1d(x, y, kind='previous')
f8 = interpolate.interp1d(x, y, kind='next')

plt.figure('Demo', facecolor='#eaeaea')
plt.subplot(221)
plt.plot(x, y, "o",  label=u"原始数据")
plt.plot(x_new, f2(x_new), label=u"临近点插值")
plt.plot(x_new, f7(x_new), label=u"前点插值")
plt.plot(x_new, f8(x_new), label=u"后点线性插值")
plt.legend()

plt.subplot(222)
plt.plot(x, y, "o",  label=u"原始数据")
plt.plot(x_new, f1(x_new), label=u"线性插值")
plt.plot(x_new, f3(x_new), label=u"零阶样条插值")
plt.plot(x_new, f4(x_new), label=u"一阶样条插值")
plt.legend()

plt.subplot(223)
plt.plot(x, y, "o",  label=u"原始数据")
plt.plot(x_new, f1(x_new), label=u"线性插值")
plt.plot(x_new, f5(x_new), label=u"三阶样条插值")
plt.legend()

plt.subplot(224)
plt.plot(x, y, "o",  label=u"原始数据")
plt.plot(x_new, f1(x_new), label=u"线性插值")
plt.plot(x_new, f6(x_new), label=u"五阶样条插值")
plt.legend()

plt.show()

不同的插值方法画在一起，对比之下效果会比较明显：

4.1.2 二维插值

二维数据，通常总是对应着一个网格，比如，经纬度网格。如果插值对象只有一个二维数组，那么我们可以用数组的行列号来构造网格。

import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['FangSong']
plt.rcParams['axes.unicode_minus'] = False

y, x = np.mgrid[-2:2:20j,-3:3:30j] # 30x20 = 600
z = x*np.exp(-x**2-y**2)
y_new, x_new = np.mgrid[-2:2:80j,-3:3:120j] # 120x80 = 9600

f1 = interpolate.interp2d(x[0,:], y[:,0], z, kind='linear') # 线性插值
f2 = interpolate.interp2d(x[0,:], y[:,0], z, kind='cubic') # 三阶样条
f3 = interpolate.interp2d(x[0,:], y[:,0], z, kind='quintic') # 五阶样条

z1 = f1(x_new[0,:], y_new[:,0])
z2 = f2(x_new[0,:], y_new[:,0])
z3 = f3(x_new[0,:], y_new[:,0])

plt.subplot(221)
plt.pcolor(x, y, z, cmap=plt.cm.hsv)
plt.colorbar()
plt.axis('equal')

plt.subplot(222)
plt.pcolor(x_new, y_new, z1, cmap=plt.cm.hsv)
plt.colorbar()
plt.axis('equal')

plt.subplot(223)
plt.pcolor(x_new, y_new, z2, cmap=plt.cm.hsv)
plt.colorbar()
plt.axis('equal')

plt.subplot(224)
plt.pcolor(x_new, y_new, z3, cmap=plt.cm.hsv)
plt.colorbar()
plt.axis('equal')

plt.show()

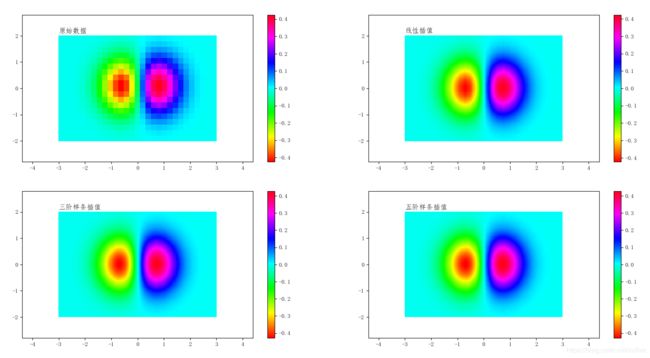
原始数据、线型插值数据、三阶插值数据、五阶插值数据的效果对比如下：

4.2 拟合

在工作中，我们常常需要在图中描绘某些实际数据观察的同时，使用一个曲线来拟合这些实际数据。所谓拟合，就是找出符合数据变化趋势的曲线方程，进而对变化趋势做出预测。

4.2.1 使用numpy.polyfit拟合

numpy.polyfit() 实现了最小二乘法，其功能是返回指定次数的多项式参数，这组参数使得多项式和样本数据的误差为最小。下面的代码，虚拟了谷神星的一段观测数据，籍此使用最小二乘法实现多项式拟合，进而推测出谷神星未来的运行轨迹。最后和虚拟的运行轨道方程比较。

# coding: utf-8

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['FangSong']
plt.rcParams['axes.unicode_minus'] = False

def f(t):
    """谷神星虚拟的运行轨道方程。我们假装不知道，仅用来验证预测结果是否准确"""
    
    t = t/7.5 -1
    return ((t**2-1)**3 + 0.5)*np.sin(2*t)

t = np.linspace(0, 20, 201) # 用于绘制实际的运行轨迹线

_x = np.linspace(0, 15, 16) # 观测数据时间序列
_y = f(_x) # 观测数据位置序列

x = np.linspace(15, 20, 6) # 待预测的时间序列

loss_list = list()
for i in range(2,16): # 从2次到15次多项式，逐一计算误差
    args = np.polyfit(_x, _y, i) # 用最小二乘法找到最佳的一组系数
    g = np.poly1d(args) # 用这组系数生成方程g(x)
    loss = np.sum(np.square(g(_x)-_y)) # 计算i次多项式拟合的误差
    loss_list.append(loss)
    print(i, loss)

k = loss_list.index(min(loss_list))+2
args = np.polyfit(_x, _y, k)
g = np.poly1d(args)

plt.figure('demo', facecolor='#eaeaea')
plt.plot(_x, _y, c='r', ls='', marker='o', label=u'观测数据')
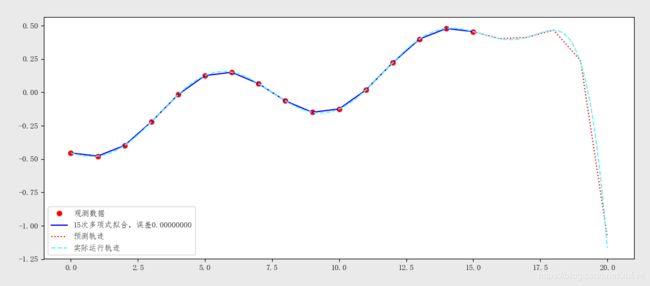
plt.plot(_x, g(_x), c='b', ls='-', label=u'%d次多项式拟合，误差%0.8f'%(k, loss_list[k-2]))
plt.plot(x, g(x), c='r', ls=':', label=u'预测轨迹')
plt.plot(t, f(t), c='#60f0f0', ls='--', label=u'实际运行轨迹')

plt.legend(loc='lower left')
plt.show()

将虚拟的运行轨道、虚拟的观测数据、拟合曲线、预测曲线绘制在一起，效果如下：

4.2.2 使用scipy.optimize.optimize.curve_fit拟合

不管曲线实际是什么样的，多项式拟合总是以一个有限次的多项式去逼近数据样本。还有一种拟合，就是我们知道曲线的标准方程，但有些系数或参数不确定，这样的拟合，也是要找到最佳系数或参数。scipy提供的拟合，需要先确定带参数的曲线方程，然后由scipy求解方程，返回曲线参数。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import optimize
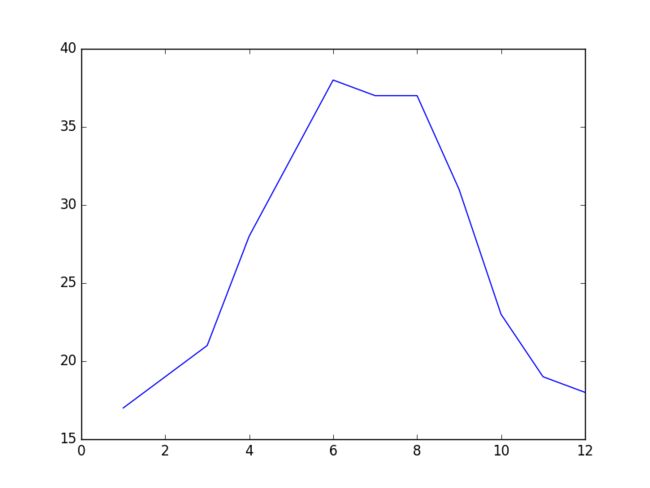
>>> x = np.arange(1,13,1)
>>> y = np.array([17,19,21,28,33,38,37,37,31,23,19,18 ])
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x04799D10>]
>>> plt.show()

可以看出，曲线近似正弦函数。构建函数y=asin(xpi/6+b)+c，使用scipy的optimize.curve_fit函数求出a、b、c的值：

>>> def fmax(x,a,b,c):
	return a*np.sin(x*np.pi/6+b)+c

>>> fita, fitb = optimize.curve_fit(fmax, x, y, [1,1,1])
>>> print fita
[ 10.93254951  -1.9496096   26.75      ]
>>> xn = np.arange(1,13,0.1)
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x04B160B0>]
>>> plt.plot(xn, fmax(xn, fita[0],fita[1],fita[2]))
[<matplotlib.lines.Line2D object at 0x04B16510>]
>>> plt.show()

4.3 求解非线性方程（组）

在数学建模中，需要对一些稀奇古怪的方程（组）求解，Matlab自然是首选，但Matlab不是免费的，scipy则为我们提供了免费的午餐！scipy.optimize库中的fsolve函数可以用来对非线性方程（组）进行求解。它的基本调用形式如下：

fsolve(func, x0)

func(x)是计算方程组误差的函数，它的参数x是一个矢量，表示方程组的各个未知数的一组可能解，func返回将x代入方程组之后得到的误差；x0为未知数矢量的初始值。

我们先来求解一个简单的方程：$ \sin(x) - \cos(x) = 0.2$

>>> from scipy.optimize import fsolve
>>> import numpy as np
>>> def f(A):
	x = float(A[0])
	return [np.sin(x) - np.cos(x) - 0.2]

>>> result = fsolve(f, [1])
array([ 0.92729522])
>>> print result
[0.92729522]
>>> print f(result)
[2.7977428707082197e-09]

哈哈，易如反掌！再来一个方程组：

$4x^2-2\sin (yz)=0$
$5y+3=0$
$yz-1.5=0$

>>> from scipy.optimize import fsolve
>>> import numpy as np
>>> def f(A):
	x = float(A[0])
	y = float(A[1])
	z = float(A[2])
	return [4*x*x - 2*np.sin(y*z), 5*y + 3, y*z - 1.5]

>>> result = fsolve(f, [1, 1, 1])
>>> print result
[-0.70622057 -0.6        -2.5       ]
>>> print f(result)
[-9.1260332624187868e-14, 0.0, 5.329070518200751e-15]

4.4 数值积分

数值积分是对定积分的数值求解，例如可以利用数值积分计算某个形状的面积。我们知道，半径为1的圆的方程可写成：

$$x^2+y^2=1$$

下面让我们来考虑一下如何计算半径为1的半圆的面积，根据圆的面积公式，其面积应该等于PI/2。单位半圆曲线可以用下面的函数表示：

$$y=\sqrt{1-x^2}$$

我们先定义一个计算根据x计算y的函数：

>>> def half_circle(x):
	return (1-x**2)**0.5

4.4.1 经典微分法

下面的程序使用经典的分小矩形计算面积总和的方式，计算出单位半圆的面积：

>>> N = 10000
>>> x = np.linspace(-1, 1, N)
>>> dx = 2.0/N
>>> y = half_circle(x)
>>> dx * np.sum(y[:-1] + y[1:]) # 面积的两倍
3.1412751679988937

4.4.2 使用定积分求解函数

如果我们调用scipy.integrate库中的quad函数的话，将会得到非常精确的结果：

>>> from scipy import integrate
>>> pi_half, err = integrate.quad(half_circle, -1, 1)
>>> pi_half*2
3.1415926535897984

4.5 图像处理

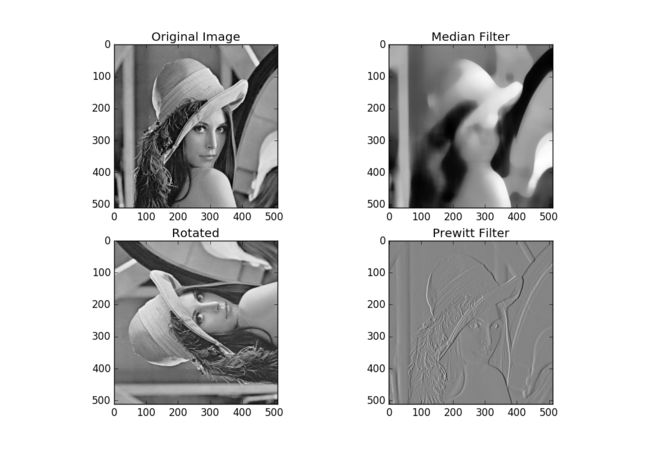
在scipy.misc模块中，有一个函数可以载入Lena图像——这副图像是被用作图像处理的经典示范图像。我只是简单展示一下在该图像上的几个操作。

1. 载入Lena图像，并显示灰度图像
2. 应用中值滤波扫描信号的每一个数据点，并替换为相邻数据点的中值
3. 旋转图像
4. 应用Prewitt滤波器（基于图像强度的梯度计算）

>>> from scipy import misc
>>> from scipy import ndimage
>>> img = misc.lena().astype(np.float32)
>>> plt.subplot(221)
>>> plt.title('Original Image')
>>> plt.imshow(img, cmap=plt.cm.gray)
>>> plt.subplot(222)
>>> plt.title('Median Filter')
>>> filtered = ndimage.median_filter(img, size=(42,42))
>>> plt.imshow(filtered, cmap=plt.cm.gray)
>>> plt.subplot(223)
>>> plt.title('Rotated')
>>> rotated = ndimage.rotate(img, 90)
>>> plt.imshow(rotated, cmap=plt.cm.gray)
>>> plt.subplot(224)
>>> plt.title('Prewitt Filter')
>>> filtered = ndimage.prewitt(img)
>>> plt.imshow(filtered, cmap=plt.cm.gray)
>>> plt.show()

5. 后记

这篇博文自2016年9月初动笔，断断续续写了5个多月。延宕这么久，除了自身懒惰的原因外，主要是因为MSN这个主题涉及的内容太过繁杂，又极其晦涩，无论怎么努力，总怕挂一漏万、贻笑大方。

现在好了，终于写完了。倘若哪位看官发现了谬误，请自行修改，顺便通知我一声；若因此文受益而想约饭、约酒，请发邮件至：[email protected]

近期有很多朋友通过私信咨询有关Python学习问题。为便于交流，我在CSDN的app上创建了“Python作业辅导”大本营，面向Python初学者，为大家提供咨询服务、辅导Python作业。欢迎有兴趣的同学使用微信扫码加入。

从博客到公众号，每一篇、每一题、每一句、每一行代码，都坚持原创，绝不复制抄袭，这是我坚守的原则。如果喜欢，请关注我的微信公众号“Python作业辅导员”。