全源最短路径算法-Floyd
一、思路
求全源最短路径可以采用单源最短路径算法实现,如采用贪心算法的Dijkstra,时间开销为|V|*O(E+VlgV),动态规划的Bellman-Ford, |V|*O(V pow 2 *E),还有Bellman的优化算法SPFA。但是呢,这样无疑会在时间开销上花费昂贵。
假设我们采用Bellman-Ford算法,
for (int i = 1; i < numOfVertex; i ++) //这里循环从1开始是因为开始节点已经存放在S中了,还有numOfVertex-1个节点要处理
{
for(int start=0;startd,c->e, c->b
{
int currentdist = distance[ start] + map[ start ][ j ];
if (currentdist < distance[ j ]) //distance[j = ]为开始到j的距离
{
distance[ j ] = currentdist;
prevVertex[ j ] = start;
}
}
}
}
} 看看矩阵的乘法:
- for(i=0;i<this->m;i++)
- for(j=0;j
- {
- for(k=0;k<this->n;k++)
- {
- m3.data[i][j]+=this->data[i][k]*m2.data[k][j];
- }
- }
二、采用动态规划思想
Floyd算法可以说是Warshall算法的扩展,三个for循环就可以解决问题,所以它的时间复杂度为O(n^3)。
Floyd算法的基本思想如下:从任意节点A到任意节点B的最短路径不外乎2种可能,1是直接从A到B,2是从A经过若干个节点X到B。所以,我们假设Dis(AB)为节点A到节点B的最短路径的距离,对于每一个节点X,我们检查Dis(AX) + Dis(XB) < Dis(AB)是否成立,如果成立,证明从A到X再到B的路径比A直接到B的路径短,我们便设置Dis(AB) = Dis(AX) + Dis(XB),这样一来,当我们遍历完所有节点X,Dis(AB)中记录的便是A到B的最短路径的距离。
但是这里我们要注意循环的嵌套顺序,如果把检查所有节点X放在最内层,那么结果将是不正确的,为什么呢?因为这样便过早的把i到j的最短路径确定下来了,而当后面存在更短的路径时,已经不再会更新了。
给出如下的代码:
#include
#include
#include
#include
using namespace std;
int map[][6] = { //定义无向图,或者有向图
{0, 6, 3, INT_MAX, INT_MAX, INT_MAX},
{6, 0, 2, 5,INT_MAX, INT_MAX},
{3, 2, 0, 3,4, INT_MAX},
{INT_MAX,5, 3, 0, 2, 3},
{INT_MAX,INT_MAX, 4, 2, 0, 5},
{INT_MAX,INT_MAX,INT_MAX,3,5,0}
};
void Dijkstra(
const int numOfVertex, /*节点数目*/
const int startVertex, /*源节点*/
int (map)[][6], /*有向图邻接矩阵*/
int *distance, /*各个节点到达源节点的距离*/
int *prevVertex /*各个节点的前一个节点*/
)
{
vector isInS; //是否已经在S集合中
isInS.reserve(0);
isInS.assign(numOfVertex, false); //初始化,所有的节点都不在S集合中 , 分配numOfVertex个字节
//step1
/*初始化distance和prevVertex数组*/
for(int i =0; i < numOfVertex; ++i)
{
distance[ i ] = map[ startVertex ][ i ]; //源节点到各个节点的距离,其中INT_MAX代表不可达
if(map[ startVertex ][ i ] < INT_MAX) //如果是可达的
prevVertex[ i ] = startVertex;
else
prevVertex[ i ] = -1; //表示还不知道前一个节点是什么
}
prevVertex[ startVertex ] = -1; //源节点无前一个节点
/*开始使用贪心思想循环处理不在S集合中的每一个节点*/
isInS[startVertex] = true; //开始节点放入S集合中
int currentVertex = startVertex;
for (int i = 1; i < numOfVertex; i ++) //这里循环从1开始是因为开始节点已经存放在S中了,还有numOfVertex-1个节点要处理
{
//step2
/*在Q中选择u到j的distance最小的一个节点, 如第一步A到C,最后目标到D*/
int minDistance = INT_MAX;
for(int j = 0; j < numOfVertex; ++j) //
{
if((isInS[j] == false) && (distance[j] < minDistance))//寻找初始currentVertexA到Q中distance最小的节点 最后为新的currentVertexC
{
currentVertex = j;
minDistance = distance[j];
}
}
isInS[currentVertex] = true;//将这个节点currentVertex放入S集合中
//step3
/*对这个新的currentVertexC做松弛计算,更新distance*/
for (int j =0; j < numOfVertex; j ++)
{
if (isInS[j] == false && map[currentVertex][j] < INT_MAX) //在Q中,有距离的为c->d,c->e, c->b
{
int currentdist = distance[ currentVertex] + map[ currentVertex ][ j ];
if (currentdist < distance[ j ]) //distance[j]为开始到j的距离
{
distance[ j ] = currentdist;
prevVertex[ j ] = currentVertex;
}
}
}
}
}
void Display(int (arr)[][6], int numOfVertex)
{
for(int i=0;i trace;
while (preVertex[index] != -1) {
trace.push(preVertex[index]);
index = preVertex[index];
}
cout << "路径:";
while (!trace.empty()) {
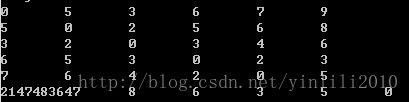
cout< 对比可以看出Dijkstra和Floyd的结果,在Floyd算法中,如果最外层的k循环只进行一圈,可能会造成中间某个点之间的路径由于中间路径没有完全更新而导致无法更新求到正确的结果。如C=1中本例的结果如下:
即5到节点0之间的距离为无穷。很明显的知道0到5的距离是9,由于这是无向图,5到0的距离也是9,所以将K循环两圈,及c<1改为c<2让他可以来的及更新值,得到如下的结果: