人工智能 一种现代方法 第7章 逻辑Agent（命题逻辑）

基于知识的Agent。第3,4章中的问题求解Agent有局限性，而且法法灵活性。
第6章介绍了 用变量赋值表示状态的思想，这是朝向正确方向的一步，使得Agent的部分工作可以独立于领域，并允许更有效的算法。

本文旨在讲清楚：
1）KBA（knowledge based agent）与逻辑
2）模型，有效性，可满足性，蕴含，推理过程
3）如何证明KB蕴含a（模型检验，逻辑等价，推理规则）

KBA(Knowledge based agent)与逻辑

KBA

基于知识的Agent的核心部件是其知识库，或称KB。
知识库(KB)：是一个语句（用知识表示语言表达，表示了关于世界的某些断言）集合。有时，当某语句是直接给定而不是推导得到的时候，我们将其尊称为公理。

Ask：查询目前所知内容
Tell：将新语句添加到知识库
二者都涉及推理，即从原有语句中推导出新语句。

KBA（Knowledge based agent），即基于知识的Agent，通过感知器，把感知信息加入知识库，向知识库询问最好改采取哪个行动，并告诉知识库它会实施该行动。

Wumpus世界

PEAS描述：

• 1）性能度量：带着金子爬出洞口+1000，掉入洞or被Wumpus吃-1000，采用一个行动-1，用掉箭-10。Agen死亡or出洞，则游戏结束。
• 2）环境：[1,1]始发为止，Wumpus，无底洞均匀分布
• 3）执行器：Agent移动，射箭。

1. Left turn,Right turn,Forward,Grab,Shoot
2. Agent可以向前移动、左转或者右转；
3. Agent碰上无底洞pit或者活着的Wumpus，它将悲惨的死去；
4. 如果Agent前方是一堵墙，那么它将不能移动；
5. 行动Grab可以用于捡起Agent所处方格内的物体；
6. 行动Shoot用于向Agent所对的方向射箭，箭向前运动直到击中Wumpus（此时Wumpus死亡）或者墙；
7. Agent只有一支箭；
8. 行动Climb用于爬出洞口；
9. Wumpus不能移动

• 4）传感器：5个
  Stench(臭气) , in,4-adjacent
  Breeze(微风), 4-adjacent
  Glitter(闪光), in
  Bump(碰撞), walking into a wall
  Scream(尖叫), wumpus killed, anywhere

1. 在与无底洞相邻的方格内，Agent能感知到微风；
2. 在与Wumpus相邻的方格内，Agent能感受到臭气；
3. 在金子所处方格，Agent能感受到闪闪金光；
4. 当Agent碰到墙时，它感知到碰撞；
5. 当Wumpus被杀死后，它发出的嚎叫声在洞穴（所有房间组成一个山洞）内的任何地方都能感受到；

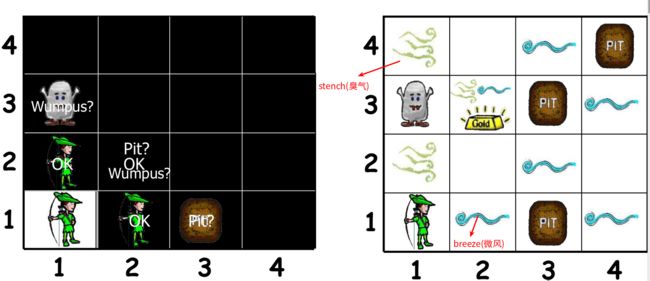
Wumpus world can be solved using logic：

• Agent在[1,1]的感知是[None,None,None,None,None](对应于(stench ,breeze,glitter,bump,scream))，因此Agent可以判断相邻的[1,2]和[2,1]是安全的，标注为ok；
• 假设Agent移动到安全的[2,1]。Agent感受到微风，因此在相邻的方格内必有一个无底洞。用于无底洞不可能在[1,1]，因此只能在[2,2]或者[3,1]或者二者都有，Pit？表示可能有无底洞；
• 此时标注ok的只有[1,2],因此Agent转身到[1,1],然后前进到[1,2];
• Agent在[1,2]感受到臭气，意味着周围一定有Wumpus。而Wumpus不可能在[1,1],也不可能在[2,2],否则Agent在[2,1]时就会感受到臭气；
• 前面讲到无底洞在[2,2]或者[3,1],而在[1,2]中感受不到微风，因此无底洞不在[2,2],故只能在[3,1];
• 现在检测到[2,2]中没有无底洞和Wumpus，因此Agent可以移动到[2,2]；
• 假定Agent转身并移动到[2,3]，感受到闪闪发光，捡到金子。

知识库KB的完备性、可靠性

一个知识库KB就是句子构成的集合。
一个模型m是一个知识库的模型当且仅当这个模型是知识库中所有句子的模型。也就是说在知识库中的所有句子在模型m下都是真的。
例如：
KB={P, P∨R}
M(KB)={“P=T,R=T”,“P=T,R=F”}

一个知识库KB是可满足的当且仅当这个知识库的模型M(KB)是非空集合。即，一个知识库KB是不可满足的当且仅当这个知识库的模型M(KB)是空集。
KB1 = {P, ￢Q∧ R} is satisfiable
KB2 = {￢P∨RP} is satisfiable
KB3 = {P, ￢P} is unsatisfiable

知识库KB蕴含α：KB ╞ α，
x+y = 4 ╞ 4 = x+y ? (yes)
x^2 +y^2 <=4 ╞ x^2 +y^2 <=16 ? (yes)
P ╞ P ∧ R ? (no)

KB ╞ α

• iff M(KB) ⊆ M(α)
• iff {KB,￢α} is unsatisfiable,
• iff KB ⇒ α is valid,
• iff KB,￢α ╞ False

推理算法i从KB中导出语句α或语句α通过i从KB导出记为: $KB{⊢}_i\alpha$
Soundness(可靠性)：对于推理过程i从KB推理出的每条语句α,都有KB╞α,则i是可靠的或真值保持的
Completeness(完备性)：对于KB蕴涵的每条语句α,推理过程i都能从KB推理出α,则i是完备的

命题逻辑：一种简单逻辑

语法

原子语句：单个命题词组成，每个命题词代表一个真或假的命题
复合句：简单语句和逻辑连接词构造而成
文字：原子命题及其否定。
互补文字：一个文字是另一文字的否定。
子句：文字的析取式。单个文字可以被视为只有一个文字的析取式，也叫单元子句。
归并：去除文字的多余副本。

5种常用逻辑连接词：
1）非 ￢，否定式
2）与 ∧，合取式
3）或 ∨，析取式
4）蕴含 ⇒或→或⊃，蕴含式
蕴含式也称为规则或if-then语句。
5）当且仅当 ⇔(英文：If and only if, 或者：iff)，双向蕴含式

语义

定义了用于判定特定模型中的语句真值的规则。在命题逻辑里面，命题词的真值只有两个——true或false。

模型：语句α在模型m中为真，称m满足α，或者m是α的一个模型。M(α)表示α的所有模型。

• “x=2,y=2” is a model of x 2 +y 2 <=16
• “x=3,y=3” is not a model of x 2 +y 2 <=16
• “P=T,Q=T” is a model of P ∧ Q.
• “P=T,Q=F” is not a model of P ∧ Q

考虑一个具有四个命题A、B、C、D的词表，对于下列语句分别有多少个模型？

• B∨C ,(2^4-1* 2^2=12)
• ￢A∨￢B∨￢C∨￢D ,(2^4-1=15)

区分⇒和╞

（1）⇒表示语言的一个组成部分
语句P⇒Q只有当P=true，Q=false时为False，其余为True。
P⇒Q等价于￢P∨Q
不要有P为真则Q为真的错觉
命题逻辑不要求P和Q之间存在相关性或因果关系。例如，语句“5是奇数蕴含北京是中国的首都”是命题逻辑的真语句
前提为假的任意蕴含都为真

（2）╞表示推理，语句间的逻辑蕴含关系
逻辑蕴含关系类似于算术：语句x=0蕴含了语句xy=0。
α╞β（蕴含）当且仅当在使α为真的每个模型中，β也为真。
α╞β 当且仅当 M(α) ⊆ M(β)
P⇒Q为假，除非P在m中为真且Q在m中为假

对任意语句α和β，α╞β 当且仅当语句α⇒β是有效的
对任意语句α和β，α╞β 当且仅当语句α∧￢β是不可满足的

命题逻辑定理的证明

逻辑推理：用蕴含推导出结论
模型检验：通过枚举所有可能的模型来检验KB为真的情况下α都为真，即M(KB) ⊆ M(α)

有效性：一个语句是有效的，如果在所有的模型中它都为真。（有效语句也叫重言式——必定为真）例如￢P∨P为有效的
对任意语句α和β，α╞β 当且仅当语句α⇒β是有效的

可满足性：如果一个语句在某些模型中为真，则可满足。
对任意语句α和β，α╞β 当且仅当语句α∧￢β是不可满足的

SAT问题：命题逻辑语句的可满足性判定。是第一个被证明为NP完全的问题。（如CSP，就是询问在某个赋值下约束是否满足的）

单调性：逻辑蕴含语句集会随着添加到知识库的信息的增长而增长。
对任意语句α和β，如果KB╞α，那么KB∧β╞α

推导和证明

推导规则：
1）假言推理规则（Modus Ponens，拉丁文）

$$\frac{\alpha \Rightarrow \beta ,\alpha }{\beta }$$

2）消去合取词

$$\frac{\alpha \wedge \beta }{\alpha }$$
3）逻辑等价
逻辑等价：如果两个语句在同样的模型集合中为真，则二者逻辑等价。

$$\alpha \iff \beta \equiv (\alpha \Rightarrow \beta )\wedge (\beta \Rightarrow \alpha )$$
$$\frac{\alpha \iff \beta }{(\alpha \Rightarrow \beta )\wedge (\beta \Rightarrow \alpha )}$$
$$\frac{(\alpha \Rightarrow \beta )\wedge (\beta \Rightarrow \alpha )}{\alpha \iff \beta }$$

任意搜索算法来找出证明序列，只需定义如下证明问题：

• 初始状态：初始KB
• 行动：行动集合由应用于语句的所有推理规则组成
• 结果：将推理规则下半部分的语句实例加入KB
• 目标：要证明的语句状态

（这叫搜索证明，是模型枚举的一个替代方法）

归结证明（只针对文字的析取式：子句）

单元归结

若每个l都是一个文字，而且$l_i$和m是互补文字，则有：
$$\frac{l1\vee ...\vee l_k,m}{l1\vee ...\vee l_{i-1}\vee l_{i+1}\vee ,...,\vee l_k}$$

全归结

$l_i$和$m_j$是互补文字：
$$\frac{l_1\vee ...\vee l_k,m_1\vee ...\vee m_n}{l_1\vee ...\vee l_{i-1}\vee l_{i+1}\vee ,...,\vee l_k\vee m_1\vee ...\vee m_{j-1}\vee m_{j+1}\vee ...\vee m_n}$$
归结规则的可靠性证明：已知$l_1\vee ...\vee l_k和m_1\vee ...\vee m_n$,则这两个子句为真。如果$l_i$为真，则由于是互补文字知$m_j$为假，则$m_1\vee ...\vee m_{j-1}\vee m_{j+1}\vee ...\vee m_n$必为真。如果$l_i$为假，则$j_1\vee ...\vee j_{i-1}\vee j_{i+1}\vee ...\vee j_k$必为真。因此，结论必定成立。

归结选取两个子句并生成一个新的子句，该子句包含除了两个互补文字以外的原始子句中的所有文字。
归结规则中每个文字只能出现一次。例如，（A∨B）和（A∨￢B）归结得(A∨A)，简化为A。

合取范式CNF

CNF：子句的合取式

析取范式DNF

归结算法-如何证明蕴含(归结演绎推理)╞

归结演绎推理是一种基于逻辑“反证法”的机械化定理证明方法。其基本思想是把永真性的证明转化为不可满足性的证明。即要证明 P→QP永真，只要能够证明P∧﹁Q 为不可满足即可。
对于知识库而言，为了证明KB ╞ α，需要证明{KB,¬α}(或KB∧¬α)是不可满足的。

步骤：
（1）将(KB∧¬α)转化成CNF。
（2）对结果子句运用归结规则，对含有互补文字的子句进行归结产生新的子句，如果该新的子句没有出现过就将其加入子句集中。
如果含有多个互补文字，需要一次性进行归结(￢B、A∨B,C∨B)归结得(A,C)而不是(A,C∨B)
（3）持续上面两步，直到：

• 没有可以添加的新语句，此时，KB不蕴含α
• 两个子句归结出空子句，则KB ╞ α

horn子句和限定子句

限定子句：受限形式的一种子句,它是指恰好只含一个正文字的析取式。例如：(A∨B∨￢C)不是限定子句，而(A∨￢B∨￢C)是限定子句。
每个限定子句可写为蕴含式

Horn子句：至多只有一个正文字的析取式。如：(A∨￢B∨￢C)和(￢A∨￢B∨￢C)都是horn子句。
Horn子句在归结下是封闭的:如果对两个Horn子句进行归结,结果依然是Horn子句。

目标子句：没有正文字的析取式。如：(￢A∨￢B∨￢C)就是目标子句。
horn子句=限定子句+目标子句

命题逻辑的前向链接和反向链接

前向链接

前向链接：从知识库中的已知事实(正文字)开始。如果蕴涵的所有前提已知，那么把它的结论加到已知事实集。持续这一过程，直到询问q被添加或者直到无法进行更进一步的推理。前向链接的运行时间是线性的。

前向链接是数据驱动推理的实例——即推理是从已知数据开始的。对于Horn KB，前向链接是

• 可靠的：每个推理本质上是分离规则的一个应用
• 完备的：每个被蕴涵的原子语句都将得以生成

反向链接

反向链接：反向链接算法正如它的名字，从查询开始进行推理。如果查询q已知为真,那么无需进行任何操作。否则,寻找知识库中那些以q为结论的蕴含式。如果其中某个蕴含式的所有前提都能证明为真(通过反向链接),则q为真。 与前向链接一样,有效实现的时间复杂度是线性的。
反向链接是一种目标制导的推理形式。

总结

本章讨论丁基于知识的 Agent,指明了如何定义一种逻辑,使得 Agent 可以使用这种逻辑对世界进行推理。
本章主要知识点如下:

• 智能Agent需要关于世界的知识以制订好的决策。
• Agent 的知识以知识表示语言的语句形式存储在Agent 的知识库中。
• 基于知识的Agent 由知识库和推理机制组成。它的工作方式是把描述世界的语句存储到它的知识库中,使用推理机制推导出新的语句,并根据这些语句来决策采取什么行动。
• 一种表示语言是通过语法和语义来定义的,其中语法指明语句的结构,而语义定义了每个语句在每个可能世界或模型中的真值。
• 语句之间的蕴涵关系对于理解推理至关紧要。如果b语句在所有a语句为真的世界中都为真,则a蕴涵b。等价定义包括语句a⇒b是有效的和语句a∧￢b是不可满足的.
• 推理是从旧语句生成新语句的过程。 可靠的推理算法只生成被蕴涵的语句;完备的算法生成所有被蕴涵的语句。
• 命题逻辑是由命题词和逻辑连接词组成的简单语言。它可以处理已知为真、已知为假或完全未知的命题。
• 给定一个固定的命题词汇表,它的可能模型集是有限的,因此蕴涵可以通过枚举模型来进行检验。用于命题逻辑的有效模型检验推理算法包括回溯和局部搜索方法,通常可以快速求解大规模的问题。
• 推理规则是用来寻找证明的可靠推理模式。消解规则是用在表示为合取范式的知识库上的完备推理算法。前向链接和反向链接都是用在Horn子句表示的知识库上的自然的推理算法。
• 局部搜索算法如WALKSAT可以用于问题求解。 这样的算法是可靠的但是不完备。
• 逻辑状态评估涉及的是维护与观察历史一致的描述可能状态集的逻辑语句。每一更新步骤要求使用环境的转移模型,转移模型可以从后继状态公理构建。
• 逻辑 Agent 的决策可以通过 SAT 求解进行:找出模型规范到达目标的未来可能的行动序列。这种方法只适用于完全可观察或无传感信息的环境。
• 命题逻辑无法扩展到无限的环境,原因是它缺之足够的表达能力来准确地处理时间、空间以及对象间关系的模式。

资源分享

实验代码下载：
https://github.com/yyl424525/AI_Homework
人工智能-一种现代方法中文第三版pdf、课件、作业及解答、课后习题答案、实验代码和报告、历年考博题下载：https://download.csdn.net/download/yyl424525/11310392