Merkle Patricia Tree (MPT) 以太坊merkle技术分析

一 传统merkle树缺陷

我的这篇博客merkle tree 分析 详细解释了merkle树的原理和作用，然而传统的merkle树有他的局限性
以下对Vitalik blog原文的翻译可以很好的阐述

传统merkle树的一个特别的限制是，它们虽然可以证明包含此交易，但无法证明任何当前的状态（例如：数字资产的持有，名称注册，金融合约的状态等）。你现在拥有了多少个比特币？一个比特币轻客户端，可以使用一种涉及查询多个节点的协议，并相信其中至少会有一个节点会通知你关于你的地址中任何特定的交易支出，而这可以让你实现更多的功能。但对于其他更为复杂的应用而言，这些远远是不够的。一笔交易影响的确切性质（precisenature），可以取决于此前的几笔交易，而这些交易本身则依赖于更为前面的交易，所以最终你可以验证整个链上的每一笔交易。为了解决这个问题，以太坊的梅克尔树的概念，会更进一步。

二 以太坊的改进

1、先说前缀树

MPT中的Patricia即patricia tree 前缀树，也叫trie或者字典树，刷过oj的同学都体验过这个数据结构的查找速度有多快，甚至超过hash
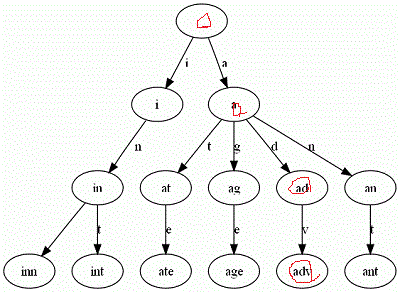
传统的前缀树如下：

上面这棵trie包含这样一组单词，inn, int, at, age, adv, ant 每个节点存储的是字符串中的谋和字符，每个从根到某个节点的路径（不一定到叶子节点）代表了一个存储的字符串，如果我想查找adv是否存在，只需要走红圈这样的路径即可

上图是一个简略视图，实际上trie每个节点是一个确定长度的数组，数组中每个节点的值是一个指向子节点的指针，最后有个标志域，标识这个位置为止是否是一个完整的字符串，并且有几个这样的字符串

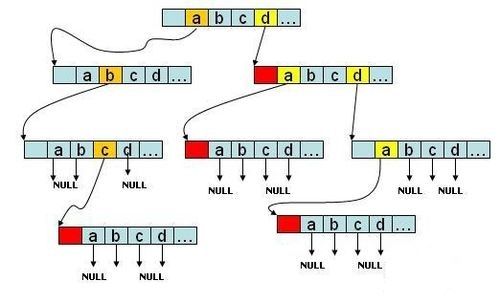
常见的用来存英文单词的trie每个节点是一个长度为27的指针数组，index0-25代表a-z字符，26为标志域

如图

2、传统trie的局限

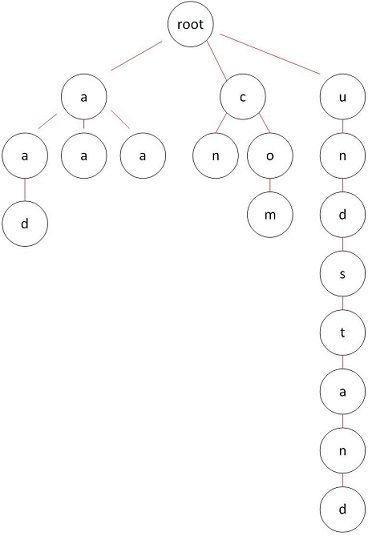
1 高度不可控

如上图所示，如果有一个字符串很长，且跟其他字符串没有公共前缀，就会形成这样的一棵极其不平衡的树，整棵树的性能会被少量的这样的字符串拖慢，并且给攻击者提供了可能

2 安全系数不高

传统的trie是由内存指针来连接节点，并且字符串的值就相当于存储在这棵树中，两者完全暴露在外，毫无安全性可言

3、以太坊漂亮的改进

1 压缩路径

传统的trie只有一种节点，该节点是一个数组，每个index是指向子节点的指针

以太坊增加了两个新的节点，称为叶节点和扩展节点，两个节点的形式一样，都是一个[key,value]的组合，原来的节点称为分支节点

key value 有没有感觉很熟悉？是的就是数据库，以太坊的数据存放在google的levelDB关系数据库中

叶子节点和扩展节点的区别在于，value 域，叶子节点的value就是字符串的值，而扩展节点的value是一个指向另一个节点的指针

详细的增删改查操作原理非常长我不在这里阐述，这篇博客 以及 这篇写的非常好，也非常详细，我只总结一些关键的东西

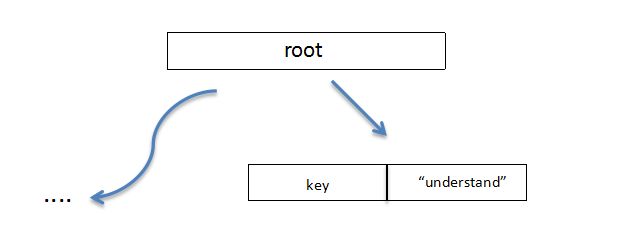
我们来看看这个两个增加的神奇节点，回想我们上面的图，当一个长长长长的字符串被插入trie很不幸又没有其他字符串与他相匹配时，会形成一个很长的路径

如今，当我们发现新加入了一个这样的节点，我们直接生成一个value为“understand”的叶子节点，长度从10直接压缩到了1!

如果再插入一个“understood”，那么我们会新建一个分支节点，不妨称为node，生成一个key为“underst”value为指向node指针的扩展节点，不妨称为extension ，指向新创建的两个叶子节点，leaf1 leaf2，value分别为“understand”和“understood”

2 安全性

MPT中的节点是一个key：value的组合，但是并直接存储值，而是经过编码的值，此处的编码方式为RLP编码，而key是RPL编码的hash值，指针依然不是内存地址，而是hash值
所有非叶节点存在levelDB数据库中

3 带来的新特性

• 树的深度是有限制的，即使考虑攻击者会故意地制造一些交易，使得这颗树尽可能地深。不然，攻击者可以通过操纵树的深度，执行拒绝服务攻击（DOS attack），使得更新变得极其缓慢。

• 树的根只取决于数据，和其中的更新顺序无关。换个顺序进行更新，甚至重新从头计算树，并不会改变根。

三 以太坊的应用

（以下引用来自巴比特翻译的Vitalik的博客）

以太坊的每一个区块头，并非只包含一颗梅克尔树，而是包含了三颗梅克尔树，分别对应了三种对象：

• 交易（Transactions）

• 收据（Receipts，基本上，它是展示每一笔交易影响的数据条）

• 状态（State）

它允许轻客户端轻松地进行并核实以下类型的查询答案：

• 这笔交易被包含在特定的区块中了么？

• 告诉我这个地址在过去30天中，发出X类型事件的所有实例（例如，一个众筹合约完成了它的目标）

• 目前我的账户余额是多少？

• 这个账户是否存在？

• 假装在这个合约中运行这笔交易，它的输出会是什么？

第一种是由交易树（transaction tree）来处理的；第三和第四种则是由状态树（state tree）负责处理，第二种则由收据树（receipt tree）处理。计算前四个查询任务是相当简单的。服务器简单地找到对象，获取梅克尔分支，并通过分支来回复轻客户端。

第五种查询任务同样也是由状态树处理，但它的计算方式会比较复杂。这里，我们需要构建下我们称之为梅克尔状态转变的证明（Merkle state transition proof）。从本质上来讲，这样的证明也就是在说“如果你在根S的状态树上运行交易T，其结果状态树将是根为S’，log为L，输出为O” （“输出”作为存在于以太坊的一种概念，因为每一笔交易都是一个函数调用，它在理论上并不是必要的）。

为了推断这个证明，服务器在本地创建了一个假的区块，将状态设为 S，并假装是一个轻客户端，同时请求这笔交易。也就是说，如果请求这笔交易的过程，需要客户端确定一个账户的余额，这个轻客户端会发出一个余额疑问。如果这个轻客户端需要检查存储在一个特定合约的特定项目，该轻客户端会对此发出针对查询。服务器会正确地“回应”它所有的查询，但服务器也会跟踪它所有发回的数据。然后，服务器会把综合数据发送给客户端。客户端会进行相同的步骤，但会使用它的数据库所提供的证明。如果它的结果和服务器要求的是相同的，那客户端就接受证明。