python判断散点是否在多边形内部

第一次在csdn上写心得，就当做自己的学习笔记吧

判断一个散点是否在多边形内部的主要依据有如下几点：

1、过散点做X轴平行线，与多边形相交。

2、左边交点数为基数，在内部，偶数在外部

3、散点在多边形上的情况 可自定义算成内部或外部

下面逐步讲解：

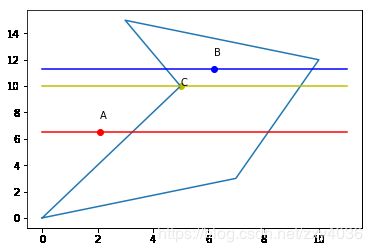
一、首先生成多边形和几个散点

import numpy as np
x1 = np.linspace(0, 5, 10)
x2 = np.linspace(5, 3, 10)
x3 = np.linspace(3, 10, 20)
x4 = np.linspace(10, 7, 30)
x5 = np.linspace(7, 0, 30)

y1 = np.linspace(0, 10, 10)
y2 = np.linspace(10, 15, 10)
y3 = np.linspace(15, 12, 20)
y4 = np.linspace(12, 3, 30)
y5 = np.linspace(3, 0, 30)

# 合并散点坐标
x = np.concatenate([x1, x2, x3, x4, x5], axis=0)
y = np.concatenate([y1, y2, y3, y4, y5], axis=0)

# 用来判定的散点
xa = 2.1
ya = 6.5
xb = 6.2
yb = 11.3
xc = 5
yc =10
pa = [xa, ya]
pb = [xb, yb]
pc = [xc, yc]

# 图形见开始
import matplotlib.pyplot as plt
plt.plot(x, y)
plt.scatter(pa[0], pa[1], c="r")
plt.text(pa[0], pa[1]+1, "A")
plt.scatter(pb[0], pb[1], c="b")
plt.text(pb[0], pb[1]+1, "B")
plt.scatter(pc[0], pc[1], c="y")
plt.text(pc[0], pc[1], "C")
plt.plot([0, 11], [pa[1], pa[1]], c="r")
plt.plot([0, 11], [pb[1], pb[1]], c="b")
plt.plot([0, 11], [pc[1], pc[1]], c="y")
plt.show()

 

 

二、确定交点

以红色的A点为例子，思路为与多边形边上的各个点的Y坐标相减，如果相交，则相邻的两个交点的差值必然一个>=0，另一个<=0，两者相乘，其积<=0

dya = y[:-1] - ya  # 往前位移一个点，如果是第一个点，则把最后一个点挪到第一个，默认是顺时针方向画图，如果是逆时针，需要修改下程序，也可以参考我另外一篇博客

dya_next =dya.copy()
dya_next[0] = dya[-1]
dya_next[1:] = dya[:-1] 

# 两者相乘

dya_mu = dya * dya_next

# 确定两个矩阵相乘为<=0的位置

negative_index = np.where(dya_mu <=0)

print(negative_index )

输出为:
(array([ 6, 58], dtype=int64),)

三、判断散点左边的交点个数，奇数在内,偶数在外

x_p = x[np.where(dya_mu <=0)] 

left_num = len(x_p[np.where(x_p< xa)])

# left_num = 0

结果为偶数，A点在外面，如果在边界上，则需要先确定是算在内部还是外部。

四、下面把过程写成函数

def is_inpolygon(ploygon_point, scatter_point, border=True):
    # 判断散点是否在多边形内部，border=True表示在边界上的也作为内部，否则作为外部
    # 输入的多边形为二维数组(x, y)，多行两列，默认顺时针，不是的话需要重新排序转换为顺时针，散点为单个
    # 1、过散点做X轴平行线，与多边形相交。
    # 2、左边交点数为基数，在内部，偶数在外面
    # 3、散点在多边形上的情况 算成内部
    # 输出True为在内部, False在外部
    
    # 1、将散点按顺时针排序
    new_pp = reorder_clockwise(polygon_point)

    # 1、确保输入的值为numpy类型
    pp = np.array(new_pp)
    sp = np.array(scatter_point)    

    # 2、如果多边形的头尾相连，去掉重复的一个点
    if (pp[0] == pp[-1]).all():
        pp = np.delete(pp, -1, axis=0)

    # 3、 确定交点，    
    x = pp[:, 0]
    y = pp[:, 1]
    px = sp[0]
    py = sp[1]
    print("x=", x)
    print("y=", y)
    print("px=", px)
    print("py=", py)
    

    # 边上的各个点的Y坐标与散点的Y坐标相减，如果相交，则相邻的两个交点的差值必然一个>=0，另一个<=0
    dy = y - py  
    
    # 需要判断多边形绘图是顺时针还是逆时针，顺时针则是后面的点向前位移一格，逆时针则是前面的点向后位移一格
    
    dy_next = dy.copy()
    dy_next[0] = dy[-1]
    dy_next[1:] = dy[:-1]
    print("dy=", dy)
    print("dy_next=", dy_next)

    # 两者相乘，其积<=0 则为相交点
    dy_mu = dy * dy_next
    print("dy_mu=", dy_mu)
    negative_index = np.where(dy_mu <=0)
    print("negative_index=", negative_index)
    # 如果有交点，判断散点左边的交点个数，奇数在内,偶数在外,
    if len(negative_index) >0 :        
        isp = pp[np.where(dy_mu <= 0)]
        print("isp=", isp)
        if not border:
            # 如果有交点与原多边形的点重合，会出现2个一样的行，删除重复的行
            isp = np.unique(isp, axis=0)            
            left_num = len(isp[np.where(isp[:, 0] <= px)]) # 计算左边点个数,包括本身
        else:
            left_num = len(isp[np.where(isp[:, 0] < px)])  # 计算左边点个数

        # 计算奇偶数
        if left_num % 2 ==0 :
            return False
        else:
            return True

    else:
        return False
  
# 测试
is_a = is_inpolygon(np.array([x, y]).T, pa)  # 输出False 
is_b = is_inpolygon(np.array([x, y]).T, pb)  # 输出True 
is_c = is_inpolygon(np.array([x, y]).T, pc)  # 边上的算成内部，输出True 
is_d = is_inpolygon(np.array([x, y]).T,  pc, False)  # 边上的算成外部，输出False