LeetCode刷题笔记(Java)---第41-60题
文章目录
- 前言
- 全部章节
- 1-18题
- 19-40题
- 41-60题
- 61-80题
- 81-100题
- 101-120题
- 121-140题
- 41. 缺失的第一个正数
- 42. 接雨水
- 43. 字符串相乘
- 44. 通配符匹配
- 45. 跳跃游戏 II
- 46. 全排列
- 47. 全排列 II
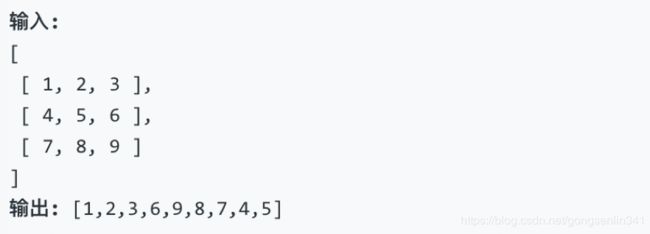
- 48. 旋转图像
- 49. 字母异位词分组
- 50. Pow(x, n)
- 51-52. N皇后
- 53. 最大子序和
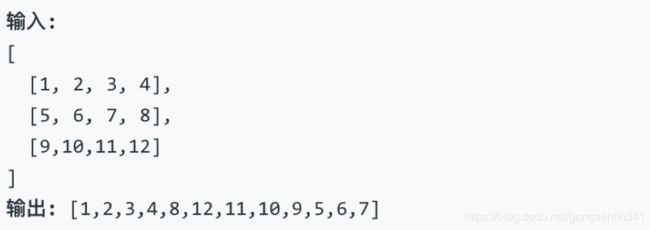
- 54. 螺旋矩阵
- 55. 跳跃游戏
- 56. 合并区间
- 57. 插入区间
- 58. 最后一个单词的长度
- 59. 螺旋矩阵 II
- 60. 第k个排列
前言
第51-52题N皇后问题,希望各位大神指点哪里还可以改进。谢谢!
全部章节
1-18题
19-40题
41-60题
61-80题
81-100题
101-120题
121-140题
41. 缺失的第一个正数
给定一个未排序的整数数组,找出其中没有出现的最小的正整数。
示例 1:

示例 2:

示例 3:

说明:
你的算法的时间复杂度应为O(n),并且只能使用常数级别的空间。
- 解答
public int firstMissingPositive(int[] nums) {
int len = nums.length;//计算数组的长度
int[] num = new int[len + 1];//新建一个数组,长度是nums的长度+1
//遍历nums,将正数且小于nums长度的值填入到该值对应下标的位置。
for (int i = 0; i < len; i++) {
if (nums[i] <= len && nums[i] > 0)
num[nums[i]] = nums[i];
}
//遍历新建的数组,找到第一个为0的值,直接返回下标,表示找到缺失的第一个正数。若没有为0的数,则直接返回num.length。表示数组中都是有序的,缺失的第一个正数等于最大值加1,即num.length。
for (int i = 1; i < num.length; i++) {
if (num[i] == 0) {
return i;
} else if (i == num.length - 1) return num.length;
}
// 若nums为空则返回1。
return 1;
}
-
分析
1.要满足算法的时间复杂度,则不可以对原数组进行排序。
2.缺失的第一个正数,一定在原数组的长度+1的范围内,所以大于原数组长度的值不需要考虑。
3.可利用新的数组,将满足上述条件的值添加进去,即可找到空缺的值。
42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
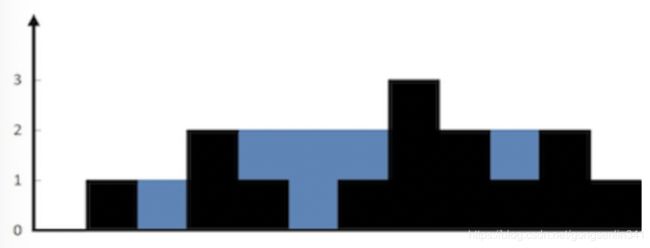
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。 感谢 Marcos 贡献此图。
- 解答
public static int trap(int[] height) {
int maxIndex = findMax(height);//求出最高的位置
int res = 0;//用于接收答案
if (height.length == 0) return 0;//若给定数组长度为0,则返回0。
int leftMax = height[0], rightMax = height[height.length - 1];//定义左边最高和右边最高,初始化为两端。
//从左边到最高位置遍历
for (int i = 1; i < maxIndex; i++) {
//若当前位置小于左边最高位置,则res加上leftMax-height[i]。
if (height[i] < leftMax) res += leftMax - height[i];
//否则左边最高位置修改为height[i]
else leftMax = height[i];
}
//同理从右边开始遍历。过程如上。
for (int i = height.length - 1; i > maxIndex; i--) {
if (height[i] < rightMax) res += rightMax - height[i];
else rightMax = height[i];
}
return res;
}
//找到最高点的位置。
public static int findMax(int[] height) {
int max = 0;
int maxi = 0;
for (int i = 0; i < height.length; i++) {
if (height[i] > max) {
max = height[i];
maxi = i;
}
}
return maxi;
}
-
分析
1.首先找到最高的位置,之后从两边开始遍历。
2.定义左边最高leftMax,然后从左开始遍历数组,只要满足当前位置小于leftMax,则说明可以接到水,因为右边有最高的那根柱子,所以只要比较与左边的最高差即可。
3.同理,从右边向最高位置遍历,累加起来即可得到答案。
43. 字符串相乘
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
- 解答
public String multiply(String num1, String num2) {
//特例判断
if (num1 == null || num2 == null || num1.length() == 0 || num2.length() == 0 || num1.equals("0")
|| num2.equals("0")) {
return "0";
}
int n1 = num1.length();//第一个字符串长度
int n2 = num2.length();//第二个字符串长度
int len = n1 + n2;//乘积的长度
int[] rst = new int[len];//用来答案。
//遍历。从个位数开始。按照乘法的计算方式。
for (int i = n1 - 1; i > -1; i--) {
int d = num1.charAt(i) - '0';
for (int j = n2 - 1; j > -1; j--) {
//除了两个数相乘还要加上进位。
int carry = d * (num2.charAt(j) - '0') + rst[i + j + 1];
//两数相乘的个位
rst[i + j + 1] = carry % 10;
//两数相乘的十位,即进位。
rst[i + j] += carry / 10;
}
}
//StringBuilder 效率更高
StringBuilder sb = new StringBuilder();
//若最高位位0,则从后一位算起。
int k = rst[0] == 0 ? 1 : 0;
for (; k < len; k++) {
sb.append(rst[k]);
}
return sb.toString();
}
-
分析
1.两数相乘的积最大的长度是两个数长度的和。
如99*99 = 9801 即 2+2=4
2.按照乘法的手算方式。两两相乘,得进位与余下的一位。
44. 通配符匹配
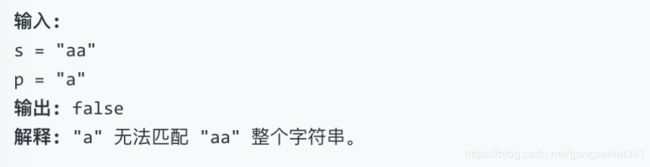
给定一个字符串 (s) 和一个字符模式 § ,实现一个支持 ‘?’ 和 ‘*’ 的通配符匹配。
说明:

示例 1:
示例 2:
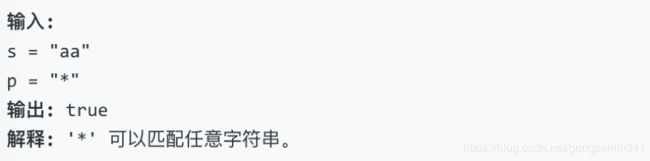
示例 3:

示例 4:

示例 5:

- 解答
public static boolean isMatch2(String s, String p) {
//dp数组,表示比较s到i和p到j的字符串是否匹配。boolean初始化默认是false;
boolean[][] dp = new boolean[s.length() + 1][p.length() + 1];
//字符串s和p都为空,表示匹配,设为true
dp[0][0] = true;
//字符串s为空,若p的第j位为‘*’,即下标j-1为‘*’
//则表示“*”匹配空字符串。
for (int j = 1; j < p.length() + 1; j++) {
if (p.charAt(j - 1) == '*') {
dp[0][j] = dp[0][j - 1];
}
}
//判断s到i和p到j的字符串匹配。
for (int i = 1; i < s.length() + 1; i++) {
for (int j = 1; j < p.length() + 1; j++) {
//若s的第i位与p的第j位相同,或p的第j位等于‘?’,则表示两位置匹配,设置dp[i][j] = dp[i - 1][j - 1]。
if (s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '?') {
dp[i][j] = dp[i - 1][j - 1];
}
//若p的第j位是“*”
else if (p.charAt(j - 1) == '*') {
//dp[i][j-1]表示“*”匹配空字符串
//dp[i-1][j]表示“*”匹配任意字符串
dp[i][j] = dp[i][j - 1] || dp[i - 1][j];
}
}
}
//返回最后的位置,表示s和p是否完全匹配
return dp[s.length()][p.length()];
}
-
分析
1.使用动态规划
dp[i][j]表示s到i位置,p到j位置是否匹配
2.初始化dp[0][0],表示两个空数组匹配,
第一行dp[0][j],表示s位空,p只要是“*”组成的则匹配
第一列dp[i][0],表示p位空,s不为空,无法匹配。
3.动态方程
若s[i]等于p[j] 或p[j]等于’?'且前一位匹配dp[i-1][j-1]等于true,则dp[i][j]=true
若p[j]等于 " * " ,且dp[i-1][j]等于true或dp[i][j-1]等于true,则dp[i][j]=true
dp[i-1][j],表示" * “与空字符匹配。
dp[i][j-1],表示” * "与非空字符匹配。
45. 跳跃游戏 II
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
public int jump(int[] nums) {
int end = 0;//用于记录边界
int maxPosition = 0;//每个位置最远可达的地方
int steps = 0;//步数
//从第一个位置出发,根据贪心原则,寻找可跳最远的地方。
for (int i = 0; i < nums.length - 1; i++) {
//找到跳的最远
maxPosition = Math.max(maxPosition, nums[i] + i);
if (i == end) { //i已经遍历到当前已知可达最远处,更新边界。步数+1。
end = maxPosition;
steps++;
//若当前边界已经最大边界,不用继续判断。
if (end >= nums.length - 1) break;
}
}
return steps;
}
-
分析
1.利用贪心原则+动态规划的原则。在一定范围内选择可跳最远点。
例如nums = [2,3,1,1,4]
起始范围在0点,只有一种情况nums[0]=2,最远可跳2个单位。
则修改边界到2,步数+1,在1-2的范围内,寻找下一个可达最远的点。
nums[i]+i,表示在i点可达最远的地方。
nums[1]+1=4,nums[2]+2=3,最远可达的点是4。
修改边界到4,步数+1。此时边界大于等于最大边界,返回步数。
46. 全排列
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
- 解答
public List<List<Integer>> permute(int[] nums) {
//用来保存答案
List<List<Integer>> res = new ArrayList<>();
//用来记录已经使用过的数字。
int[] visited = new int[nums.length];
//回溯算法
backtrack(res, nums, new ArrayList<>(), visited);
return res;
}
private void backtrack(List<List<Integer>> res, int[] nums, ArrayList<Integer> tmp, int[] visited) {
//当组合内元素的数量等于数组的长度,则说明找到符合条件的组合,添加到答案中。
if (tmp.size() == nums.length) {
res.add(new ArrayList<>(tmp));
return;
}
//遍历数组。
for (int i = 0; i < nums.length; i++) {
//找到还没被用过的数字
if (visited[i] == 1) continue;
//标记为已经使用
visited[i] = 1;
//将该数字加入到组合中
tmp.add(nums[i]);
//递归调用回溯算法。
backtrack(res, nums, tmp, visited);
//回溯,将这一层递归中加入到组合中的数字拿出来
//标记为未被使用。
visited[i] = 0;
//从组合中移除。
tmp.remove(tmp.size() - 1);
}
}
-
分析
1.类似这种有规律的排列组合的问题,可以用回溯的模版来实现。
2.已经做过的题目中有39和40题。方法流出整体相似。
3.回溯算法关键在于:不满足条件就返回到上一步。此题目就是将刚加入的数字去除。
47. 全排列 II
给定一个可包含重复数字的序列,返回所有不重复的全排列。
- 解答
public static List<List<Integer>> permuteUnique(int[] nums) {
//用于接收答案
List<List<Integer>> res = new ArrayList<>();
//用于记录数字是否被使用过
int[] visited = new int[nums.length];
//对数组进行排序,方便后面去重
Arrays.sort(nums);
//调用回溯算法
backtrack3(res, nums, new ArrayList<>(), visited);
return res;
}
public static void backtrack3(List<List<Integer>> res, int[] nums, ArrayList<Integer> tmp, int[] visited) {
//若已找到组合,则添加到答案中。
if (tmp.size() == nums.length) {
res.add(new ArrayList<>(tmp));
return;
}
//遍历数组
for (int i = 0; i < nums.length; i++) {
//若当前添加的数字和前一个一样,并且前一个还没有被使用过则跳过。下面分析会解释。
if (i > 0 && nums[i] == nums[i - 1] && visited[i - 1] != 1) continue;
//若当前数字已经使用过则跳过
if (visited[i] == 1) continue;
//标记该数字已使用
visited[i] = 1;
//添加到组合中
tmp.add(nums[i]);
//递归调用算法。
backtrack3(res, nums, tmp, visited);
//回溯,刚加入的数字拿出,标记为未被使用
visited[i] = 0;
//从组合中删去该数字。
tmp.remove(tmp.size() - 1);
}
}
-
分析
1.这题相对于上一题的难点在于去重。
方法一,可以使用Set来实现去重,简单暴力。
方法二,如同上面代码一样。加一句判断即可。
if (i > 0 && nums[i] == nums[i - 1] && visited[i - 1] != 1)
假设给定数组[1,2,1],事先排序后为[1,1,2]
nums[i] == nums[i-1]表示前后数字一样。此时就要考虑两种情况。
1.是按照排序后的数组按顺序添加的数字。第一个1加入到组合中。第二个1,根据这一条语句判断是和前一个数字一样的。如果此时没有visited[i - 1] != 1 这一句的话。则会跳过第二个1。而加上才会得到[1,1,2]的组合。
2.不是按照顺序添加的数字。算法多次递归回溯后。组合中会出现一种情况,那就是组合为空,第二个1准备加入组合中。根据
if (i > 0 && nums[i] == nums[i - 1] && visited[i - 1] != 1)
判断前一个1位被使用过,则不会加入到组合中。这样就避免了出现两组[1,1,2]的情况。
48. 旋转图像
给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。
说明:
你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
- 解答
public static void rotate(int[][] matrix) {
int len = matrix.length;
//矩阵转置
for (int i = 0; i < len; i++) {
for (int j = i + 1; j < len; j++) {
int tmp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = tmp;
}
}
//左右对称变换
for (int i = 0; i < len; i++) {
for (int j = 0; j < len / 2; j++) {
int tmp = matrix[i][j];
matrix[i][j] = matrix[i][len - j - 1];
matrix[i][len - j - 1] = tmp;
}
}
}
-
分析
1.旋转90度相当于先转置后镜像对称。
49. 字母异位词分组
给定一个字符串数组,将字母异位词组合在一起。字母异位词指字母相同,但排列不同的字符串。
-
所有输入均为小写字母。
-
不考虑答案输出的顺序。
-
解答
public static List<List<String>> groupAnagrams(String[] strs) {
//用于存储不同的组合
//key 表示不同类型的字符串,相同字符组成的字符串放入对应的value中。
HashMap<String,ArrayList<String>> map=new HashMap<>();
//遍历字符串数组
for(String s:strs){
//字符串转成字符数组
char[] ch=s.toCharArray();
//排序
Arrays.sort(ch);
//转成排序后的字符串
String key=String.valueOf(ch);
//若map中步包含此key,则将其存入map中
if(!map.containsKey(key)) map.put(key,new ArrayList<>());
//将相同字母组成的字符串存入对应的key映射的value中。
map.get(key).add(s);
}
return new ArrayList(map.values());
}
-
分析
1.利用HashMap,key唯一的特点。可以将不同字母组成的字符串作为key,符合相同字母组成的字符串加入到对应的value中。
2.排序是为了相同的字母组合得到相同的字符串结果。
50. Pow(x, n)
实现 pow(x, n) ,即计算 x 的 n 次幂函数。
- -100.0 < x < 100.0
- n 是 32 位有符号整数,其数值范围是 [−231, 231 − 1] 。
- 解答
public double myPow(double x, int n) {
double res = 1.0;
for (int i = n; i != 0; i /= 2) {
if (i % 2 != 0) {
res *= x;
}
x *= x;
}
return n < 0 ? 1 / res : res;
}
-
分析
1.刚开始使用递归做,发现会栈溢出,改用for循环。
2.每次将i除以2,若i是偶数,则将底数*底数。
例如2的8次方 = 2的2次方的4次方 = 4的4次方
若i是奇数,则将答案乘以x。即将n-1.
例如2的9次方 = 2 * 2的8次方。
3.根据指数n是否小于0,返回结果。
51-52. N皇后
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
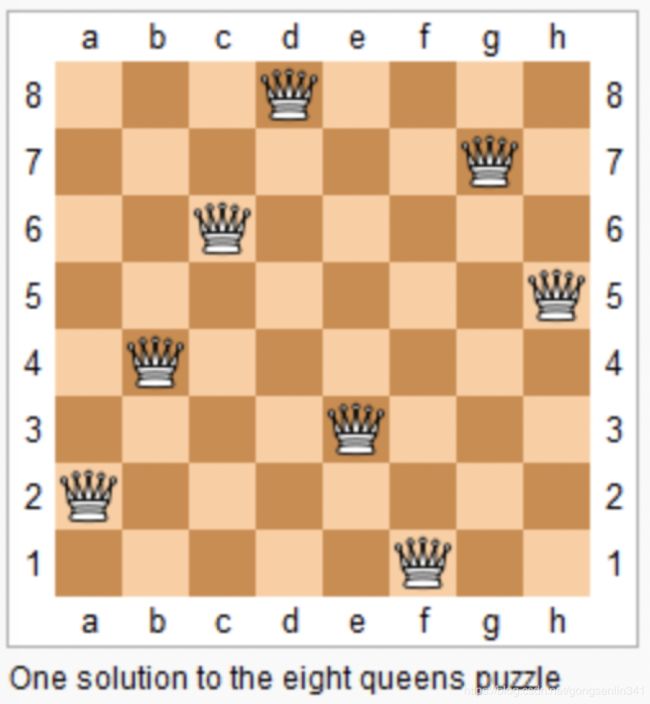

上图为 8 皇后问题的一种解法。
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
示例:
public static List<List<String>> solveNQueens(int n) {
List<List<String>> res = new ArrayList<>();//用于存储答案
boolean[][] visited = new boolean[n][n];//用于标记已经使用的位置。
//回溯算法
backtrack4(res, new ArrayList<>(), visited);
return res;
}
//回溯算法
public static void backtrack4(List<List<String>> res, List<String> tmp, boolean[][] visited) {
//当tmp的大小等于棋子的数量,说明满足条件,将其加入答案中
if (tmp.size() == visited.length) {
res.add(new ArrayList<>(tmp));
}
//遍历行
for (int row = 0; row < visited.length; row++) {
//若当前行已经越过tmp的大小。则结束行遍历。
//因为棋子是一行一行的放入的,若当前行的前面有一行没有放棋子,则不用考虑之后的行。
if (row > tmp.size()) break;
//遍历列
for (int i = 0; i < visited.length; i++) {
//判断是否可以填入棋子
if (check(visited, row, i)) {
//将其标记为已使用
visited[row][i] = true;
//得到这一行的结果
String string = add(i, visited.length);
//添加到组合中
tmp.add(string);
//递归
backtrack4(res, tmp, visited);
//回溯,拿回棋子。
visited[row][i] = false;
tmp.remove(string);
}
}
}
}
//判断是否可以放入棋子
public static boolean check(boolean[][] visited, int row, int column) {
//判断放入棋子的行列是否已经有棋子。
for (int i = 0; i < visited.length; i++) {
if (visited[row][i]) return false;
if (visited[i][column]) return false;
}
//下面两个for是判断该位置的X型的线上是否有棋子。
for (int i = 0; i < row; i++) {
if (row - i - 1 >= 0) {
if (column - i - 1 >= 0) {
if (visited[row - i - 1][column - i - 1])
return false;
}
if (column + i + 1 < visited.length) {
if (visited[row - i - 1][column + i + 1])
return false;
}
}
}
int index = 0;
for (int i = row + 1; i < visited.length; i++) {
if (row + index + 1 < visited.length) {
if (column - index - 1 >= 0) {
if (visited[row + index + 1][column - index - 1])
return false;
}
if (column + index + 1 < visited.length) {
if (visited[row + index + 1][column + index + 1])
return false;
}
}
index++;
}
return true;
}
//得到放入棋子后这一行的字符串表示
public static String add(int index, int len) {
StringBuilder stringBuilder = new StringBuilder();
for (int i = 0; i < len; i++) {
if (i != index)
stringBuilder.append(".");
else stringBuilder.append("Q");
}
return stringBuilder.toString();
}
-
分析
1.这也是一种排列组合的问题,使用回溯来做。
2.主要考虑棋子是否可以放入。
3.if (row > tmp.size()) break;这一句代码一开始没加,思考了好久才发现问题。这里回溯法棋子放入是要按照行顺序的。所以如果遍历的此行已经比已经得到的组合数大2,就说明有一行没有添加棋子,则直接结束即可。
4.52题输出组合数量即可。
53. 最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
- 解答
public int maxSubArray(int[] nums) {
int res = nums[0];//用于存储答案
int sum = 0;//每一步的和
for (int i = 0; i < nums.length; i++) {
if (sum > 0){//若子序列和大于0,则加上下一位数字
sum += nums[i];
}else//若小于等于零,则等于这一位数字。
sum = nums[i];
//每次组合变动都比较一下最大值。保存下来。
res = Math.max(res,sum);
}
return res;
}
-
分析
1.最大子序列和的第一个数字必定是大于0的。
2.在已找到一个数字的基础上,继续扩大范围,每一次的扩大都与答案进行比较,保留下更大的和。
3.当组合小于0的时候,新的组合开始。跳过组合中的正值。是因为若组合中的第一位去掉了。那么剩余的数字之和会更小。所以不用考虑当前组合中的正数。从下一位正数开始即可。
54. 螺旋矩阵
给定一个包含 m x n 个元素的矩阵(m 行, n 列),请按照顺时针螺旋顺序,返回矩阵中的所有元素。
- 解答
public static List<Integer> spiralOrder(int[][] matrix) {
List<Integer> res = new ArrayList<>();
int row = matrix.length;
if (row == 0) return res;
int column = matrix[0].length;
add(matrix, row, column, 0, res);
return res;
}
// number 表示第几层从外向里,rowNumber和columnNumber表示行数与列数。
public static void add(int[][] matrix, int rowNumber, int columnNumber, int number, List<Integer> res) {
//这一层的上面一行
for (int i = number; i < columnNumber - number; i++) {
res.add(matrix[number][i]);
}
//这一层的右侧一列(除上下两端)
for (int i = number + 1; i <= rowNumber - number - 2; i++) {
res.add(matrix[i][columnNumber - number - 1]);
}
//这一层的下面一行
if (rowNumber - 2 * (number + 1) >= 0)
for (int i = columnNumber - number - 1; i >= number; i--) {
res.add(matrix[rowNumber - 1 - number][i]);
}
//这一层的左侧一列(除上下两端
if (columnNumber - 2 * (number + 1) >= 0)
for (int i = rowNumber - 2 - number; i > number; i--) {
res.add(matrix[i][number]);
}
//若还有下一层,则进入下一层。
if (columnNumber - 2 * (number + 1) > 0 && rowNumber - 2 * (number + 1) > 0)
add(matrix, rowNumber, columnNumber, ++number, res);
}
-
分析
1.用递归来实现,根据回字形来层层输出,每一次完成一层直到最里层。
2.关键在于回字形输出和行列以及层数之间的关系。
55. 跳跃游戏
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个位置。
- 解答
public static boolean canJump(int[] nums) {
int max = nums[0];//当前可走最远距离。
if (nums.length == 0 || nums.length == 1) return true;
// 遍历数组
for (int i = 0; i < nums.length; i++) {
//若当前位置加其可走的最远距离 大于 当前最远距离,并且当前位置小于当前最远距离,更新当前位置最远距离。
if (i + nums[i] > max && i <= max)
max = i + nums[i];
//若当前可走最远距离大于等于数组最后一个位置,则返回true
if (max >= nums.length - 1) return true;
}
//遍历结束 当前最远距离不能到达数组末尾。返回false。
return false;
}
-
分析
1.数组是非负整数,从第一个位置开始。若数组长度为0或1,直接返回true。表示可达。
2.根据遍历数组,可以计算出可以走的最远距离。根据最远距离和数组长度判断,得出是否可达数组末尾。
56. 合并区间
给出一个区间的集合,请合并所有重叠的区间。
- 解答
public static int[][] merge(int[][] intervals) {
//根据区间的左边排序,重写compare方法。
Arrays.sort(intervals,new Comparator<int[]>(){
@Override
public int compare(int[] a,int[] b){
return a[0]-b[0];
}
});
//特殊情况判断。长度为0或1,不需合并区间。
if (intervals.length == 1 || intervals.length == 0) return intervals;
List<int[]> res = new ArrayList<>();
//用于记录临时的区间
int left = intervals[0][0];
int right = intervals[0][1];
for (int i = 1; i < intervals.length; i++) {
//若新的区间左边大于记录的临时区间的右边,则将临时区间加入答案中。
//更新临时区间。
if (intervals[i][0] > right) {
int[] tmp = new int[]{left, right};
res.add(tmp);
left = intervals[i][0];
right = intervals[i][1];
}
//若新的区间左边包含在临时区间中,右边在区间歪,则根须临时区间的右侧。
else if (intervals[i][0] <= right && intervals[i][1] > right)
right = intervals[i][1];
}
//最后一个临时区间还未加入答案中。加入!
int[] tmp = new int[]{left, right};
res.add(tmp);
return (int[][]) res.toArray(new int[0][]);
}
-
分析
1.先根据区间的左侧进行排序
2.判断区间之间是否重叠,合并他们
3.用List可以添加数组的大小。不用事先知道需要多大的数组空间。
57. 插入区间
给出一个无重叠的 ,按照区间起始端点排序的区间列表。
在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。
- 解答
public static int[][] insert(int[][] intervals, int[] newInterval) {
int n = intervals.length;
int[] last = newInterval;//以要插入的区间作为基准。
List<int[]> res = new ArrayList<>();
//迭代已有的区间数组。
for (int[] curr:intervals) {
//寻找和基准区间重叠的区间进行合并。
if (last != null && last[1] >= curr[0] && last[0] <= curr[1]){
last[0] = Math.min(curr[0], last[0]);
last[1] = Math.max(curr[1], last[1]);
} else {
// 当基准区间在某区间之外,则将基准区间添加如答案中。
if(last != null && last[1] < curr[0]) {
res.add(last);
last = null;
}
//其余的区间插入。
res.add(curr);
}
}
if(last != null) res.add(last);
return res.toArray(new int[res.size()][]);
}
-
分析
1.寻找可以和插入数组合并的区间,包括合并后的新区间与其余的区间重叠的合并。一直到没有重叠区间。
2.其余的区间只需要原封不动的插入。
58. 最后一个单词的长度
给定一个仅包含大小写字母和空格 ’ ’ 的字符串 s,返回其最后一个单词的长度。如果字符串从左向右滚动显示,那么最后一个单词就是最后出现的单词。
如果不存在最后一个单词,请返回 0 。
说明:一个单词是指仅由字母组成、不包含任何空格字符的 最大子字符串。
- 解答
public static int lengthOfLastWord(String s) {
int length = 0;//用于记录最后一个单词的长度
//从后往前遍历
for (int i = s.length() - 1; i >= 0; i--) {
//不是空格则长度加一
if (s.charAt(i) != ' ') {
length++;
}
//当遇到空格,并且记录的长度不为0的时候,说明最后一个单词已经找到。直接返回此时记录的长度。
else if (length != 0) {
return length;
}
}
//遍历结束返回长度,说明第一个单词也是最后一个单词。
return length;
}
-
分析
1.此题很简单,找出最后一个单词。
2.从后开始遍历,去掉空格,因为测试用例中有末尾带空格的字符串,遇到字母记录长度。当再此遇到空格返回长度。
59. 螺旋矩阵 II
给定一个正整数 n,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的正方形矩阵。
- 解答
public static int[][] generateMatrix(int n) {
int[][] res = new int[n][n];
//用于生成数字。
generate(res,0,1,n);
return res;
}
// 参数第一个是接收答案存放数字的矩阵,第二个参数是当前层(从0开始,层表示从外向里,回字形的一层),第三个参数是记录数字,第四个参数是给定的正整数n。
public static void generate(int[][] matrix, int index, int number, int n) {
//这一层的最上面一行
for (int i = index; i < matrix.length - index; i++)
matrix[index][i] = number++;
//表示,若当前层不止一行
if ((index+1) * 2 <= n) {
//这一层右边一列(除上下两端)
for (int i = index + 1; i < matrix.length - index - 1; i++) {
matrix[i][matrix.length - index - 1] = number++;
}
//这一层下面的一行
for (int i = matrix.length - index - 1; i >= index; i--) {
matrix[matrix.length - index - 1][i] = number++;
}
//这一层左边的一列(除上下两端)
for (int i = matrix.length - index - 2; i > index; i--) {
matrix[i][index] = number++;
}
}
//若这一层里还有包裹的层,则递归,层数+1,number继承下去。
if (index * 2 < n) {
generate(matrix, ++index, number, n);
}
}
-
分析
1.和之前的螺旋矩阵1,有相似之处,相比较来说更加的简单。因为矩阵是一个正方形。每一层都是正方形构成。
2.除了层的上面一行,其余的三边,可以根据判断(index+1) * 2 <= n是否成立,来确定。
3.递归调用,层层按照题目要求填入数字即可。
60. 第k个排列
给出集合 [1,2,3,…,n],其所有元素共有 n! 种排列。
按大小顺序列出所有排列情况,并一一标记,当 n = 3 时, 所有排列如下:

给定 n 和 k,返回第 k 个排列。
说明:
给定 n 的范围是 [1, 9]。
给定 k 的范围是[1, n!]。
- 解答
方法一:
public String getPermutation(int n, int k) {
List<String> list = new ArrayList<>();
backtrack(list, new StringBuilder(), n, new int[n], k);
return list.get(k - 1);//列表是从0开始的 所以第k个就要取k-1.
}
//第一个参数,用来记录数字排列情况;第二个参数,用来记录当前组合;第三个参数用来记录n个数字;第四个参数用来记录数字是否被使用过。最后一个参数是记录要寻找的第k个组合。
public void backtrack(List<String> list, StringBuilder tmp, int n, int[] visited, int k) {
//当前组合满足长度n,则加入排列组合集合中。
if (tmp.length() == n) {
list.add(tmp.toString());
}
//当前集合中已经有k个组合,则不再进行递归。
if (list.size() == k) return;
//遍历数字。
for (int i = 0; i < n; i++) {
//若没有被使用过,则加入当前组合。
if (visited[i] != 1) {
tmp.append(i + 1);
visited[i] = 1;
//递归
backtrack(list, tmp, n, visited, k);
//回溯,去除刚加入的数字。
visited[i] = 0;
tmp.delete(tmp.length() - 1, tmp.length());
}
}
}
方法二:
public String getPermutation2(int n, int k) {
int[] digit = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
List<Integer> digitList = Arrays.stream(digit).boxed().collect(Collectors.toList());
int[] factor = {1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880};
StringBuilder sb = new StringBuilder();
k--;
while (n > 0) {
int val = k / factor[n - 1];
sb.append(digitList.get(val + 1));
digitList.remove(val + 1);
k = k % factor[n - 1];
n--;
}
return sb.toString();
}
-
分析
1.之前说过这种排列组合的题目可以通过回溯来实现,方法一,就是使用回溯来实现的,利用回溯得到全排列。返回第k个。
2.为了避免超时,所以回溯中加一个终止条件,当已找到前k个排列就停止。
3.方法二是使用的逆康托展开,
感兴趣的小伙伴可以看以下这篇博客。算法基础:康托展开与逆康托展开