关系数据理论

关系数据理论

本篇文章记录了第十五次作业

---

 关系数据理论指的是关系数据库的规范化理论。这一理论是用来规范数据库模式的。落到实践层面来说，就是对数据库里面的这些表应该怎么建才好的一种理论。比如在之前遇到的的学生-选课-课程表中，我们有很多属性，而哪些属性应该组成几个什么样的表才能使我们这个数据库最优、出现问题最少呢？这就是我们要研究的问题。

---

规范化(normalization)

函数依赖

 要了解关系数据库的规范化理论，我们首先要了解函数依赖这一关系。
 设R(U)是一个属性集U上的关系模式，X和Y是U的子集。若对于R(U)的任意一个可能的关系r，r 中不可能存在：两个元组在X上的属性值相等，而在Y上的属性值不等， 我们则称“X函数确定Y”或“Y函数依赖于X”，记作X→Y。否则记作X$\nrightarrow$Y。
 简单来说，这里两者相当于形成了一种一一对应的函数关系，我们称这种关系为函数依赖。
 函数依赖有平凡函数依赖和非平凡函数依赖，但我们在在这里基本不讨论平凡函数依赖。

完全/部分/传递函数依赖

 对于非平凡函数依赖，我们还分为完全函数依赖、部分函数依赖和传递函数依赖：
 在R(U)中，如果X→Y，并且对于X的任何一个真子集X’, 都有 $X’\nrightarrow Y$, 则称Y对X完全函数依赖，记作$X\stackrel{F}{\to }Y$。若X→Y，但Y不完全函数依赖于X，则称Y对X部分函数依赖，记作$X\stackrel{P}{\to }Y$
 什么意思呢？我们举一个例子。
在关系SC(Sno, Cno, Grade)中，有：
  Sno $\nrightarrow$ Grade，Cno $\nrightarrow$ Grade
 因此：(Sno, Cno) $\stackrel{F}{\to }$Grade
  (Sno, Cno)$\stackrel{P}{\to }$Sno
  (Sno, Cno)$\stackrel{P}{\to }$Cno
 不难发现，部分函数依赖的例子里面Sno其实只需要Sno就可以确定，但由于候选码有俩，所以很尴尬。这样强行带着就属于部分函数依赖，反之则是完全函数依赖。
 至于传递函数依赖，定义如下：
 在R(U)中，如果X→Y(Y⊈X)，Y$\nrightarrow$X，Y→Z，Z⊈Y, 则称Z对X传递函数依赖(transitive functional dependency)。记为：X $\stackrel{传递}{\to }$ Z。 如果Y→X, 即X←→Y，则Z直接依赖于X，而不是传递函数依赖。
 传递函数依赖比较容易理解，需要注意的是需要Y$\nrightarrow$X,否则就不是传递函数依赖了。

---

范式

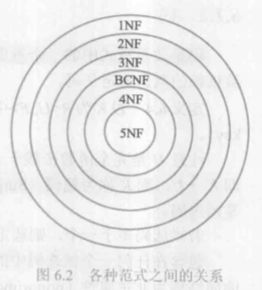
 刚刚说了半天就是为了现在的范式打基础。为了规范化，科学家提出了范式(normal form)的概念。**满足某种程度要求的关系叫做范式。**到现在我们有1NF、2NF、3NF、BCNF、4NF和5NF这几种范式。各种范式分关系为5NF $\subset$ 4NF $\subset$ BCNF $\subset$ 3NF$\subset$ 2NF $\subset$ 1NF。这些范式是建立在函数依赖/多值依赖的基础上的。
 一个低一级范式的关系模式通过模式分解(schema decomposition)可以转换为若干个高一级范式的关系模式的集合，这种过程就叫规范化(normalization)。

1NF

 满足最低要求，即存在关系的关系即使1NF，第一范式，不多说。

2NF

 若关系模式R∈1NF，并且每一个非主属性都完全函数依赖于任何一个候选码，则R∈2NF

3NF

 设关系模式R∈1NF,若R中不存在这样的码X、属性组Y及非主属性Z（Z ⊇ Y）, 使得X→Y，Y→Z成立，Y$\nrightarrow$X不成立，则称R ∈ 3NF。

BCNF

 设关系模式R∈1NF，若X →Y且Y ⊆ X时X必含有码，则R∈BCNF。换言之，在关系模式R中，如果每一个决定属性集都包含候选码，则R∈BCNF。

4NF

 关系模式R∈1NF，如果对于R的每个非平凡多值依赖X→→Y（Y ⊈ X），X都含有码，则R∈4NF。

5NF

 如果关系模式R中的每一个连接依赖均由R的候选码所隐含，则称此关系模式符合第五范式。

习题

1、建立一个关于系、学生、班级、学会等诸信息的关系数据库

 描述学生的属性有：学号、姓名、出生年月、系名、班号、宿舍区；
 描述班级的属性有：班号、专业名、系名、人数、入校年份；
 描述系的属性有：系名、系号、系办公室地点、人数；
 描述学会的属性有：学会明、成立年份、地点、人数。
 有关语义如下：一个系有若干专业，每个专业每年只招一个班，每个班有若干学生。一个系的学生住在同一宿舍区。每个学生可参加若干学会。学生参加某学会有一个入会年份。
 请给出关系模式，指出是否存在传递函数依赖，对于函数依赖左部是多属性的情况，讨论函数依赖是完全函数依赖还是部分函数依赖。 指出个关系的候选码、外部码，并说明是否全码存在。
 

解答：

 这里我们先把基本的关系模式建立起来。
 学生: S(Sno,Sname,Sdate,Dept,Cno,Sloc);
 班级: C(Cno,Maj,Dept,Cnum,Cyear);
 系: D(Dept,Dno,Dloc,Dnum);
 学会 A(Aname,Ayear,Aloc,Anum);
 
由一个系有若干专业，每个专业每年只招一个班，每个班有若干学生，我们知道Maj→Dept,(Cyear,Maj)→Cno,Sno→Cno;
由一个系的学生住在同一宿舍区，得Dept→Sloc;
由每个学生可参加若干学会。学生参加某学会有一个入会年份，我们得(Aname,Sno)->Adate.这时候就发现我们还得整个学生-学会的表。
 有S-A(Sno,Aname,Adate);
 
对于S关系，我们有：Sno→Sname,Sno→Sdate,Sno→Cno,Cno→Dept,Dept→Sloc;
对于C关系，我们有：Cno→Maj,(Maj,Cyear)→Cno,Cno→Cnum,Cno→Cyear,Maj→Dept;
对于D关系，我们有：Dept→Dno,Dno→Dept,Dno→Dloc,Dno→Dnum;
对于A关系，我们有：Aname→Ayear,Aloc,Anum;
S-A中(Sno,Aname)→Adate.
 
 那么开始解决第一个问题：是否有传递依赖？
 在S中，很明显，有。
因为Sno→Cno,Cno→Dept,故Sno和Dept存在传递函数依赖。又Dept→Sloc，所以Sno和Sloc之间，以及Cno和Sloc也有传递函数依赖
 在C中，Cno→Maj,Maj→Dept，故Cno和Dept又传递函数依赖。
 D、A、S-A中都没有传递函数依赖。
 第二个问题：对于函数依赖左部是多属性的情况，讨论函数依赖是完全函数依赖还是部分函数依赖？
 手里有两个左边是多属性的：(Sno,Aname)→Adate,以及(Maj,Cyear)→Cno，很明显二者都是完全函数依赖不是部分函数依赖。
 第三个问题：说出候选码，外码和全码。
 S中候选码明显是Sno(学号)，外码有Cno和Dept，没有全码。
 C中候选码是Cno(班号)和(Maj,Cyear),外码为Dept，同样没有全码。
 D中候选码是Dno(系号)以及Dept(系名),没有外码全码。
 A中只有候选码Aname。
 S-A中候选码是(Sno,Aname),外码是Sno和Aname，没有全码。
 

2、有关系模式R(A,B,C,D,E),回答下面各个问题：

（1）若A是R的候选码，具有函数依赖BC→DE，那么在什么条件下R是BCNF？
（2）如果存在函数依赖A→B，BC→D，DE→A，列出R的所有码。
（3）如果存在函数依赖A→B，BC→D，DE→A，R属于3NF还是BCNF。

解答

（1）A是候选码，若A→BC，那么是2NF不是3NF。所以我们要使传递函数依赖消失。我们加上BC→A，这样不符合传递函数依赖的定义了，因此R成了3NF。又A是唯一决定因素，此时R是BCNF。
故条件为A→BC,BC→A。
（2）此时有F={A→B，BC→D，DE→A)，码有ACE,CDE,BCE.
（3）存在决定因素里面不包含码的情况，故是3NF而不是BCNF。

3、下面哪些结论是正确的？哪些是错误的？

（1）任何一个二目关系是属于3NF的。
  正确。
（2）任何一个二目关系是属于BCNF的。
  正确。
（3）任何一个二目关系是属于4NF的。
  正确。
（4）当且仅当函数依赖A→B在R上成立，关系R(A,B,C)等于其投影R₁(A,B)和R₂(A,C)的连接。
  错误，反之是不成立的。当且仅当函数依赖A→→B在R上成立，关系R（A,B,C）等于其投影R1（A,B）和度R2（A,C）的连接。
（5）若R.A→R.B,R.B→R.C,则R.A→R.C。
  正确。
（6）若R.A→R.B,R.A→R.C,则R.A→R.(B,C)。
  正确。
（7）若R.B→R.A,R.C→R.A,则R.(B,C)→R.A。
  正确。
（8）若R.(B,C)→R.A,则R.B→R.A,R.C→R.A。
  错误，如SC(Sno,Cno,Grade),(Sno,Cno)→Grade,but Sno↛ Grade,Cno↛ Grade.

4、证明：

（1）如果R是BCNF关系模式，则R是3NF关系模式，反之则不然。
  若R是BCNF，则X →Y且Y ⊆ X时X必含有码.假设R不是3NF，那么其中必定存在传递函数依赖，使得BCNF的性质(X中不一定含有码)不一定成立，故若R是BCNF，则也是3NF。反之，若F仅仅是3NF，那么不一定满足BCNF条件，故不然。
（2）如果R是3NF关系模式，则R一定是2NF关系模式。
  若R是3NF，则传递不存在函数依赖，假设R不是2NF，那么R中不存在每一个非主属性都完全函数依赖于任何一个候选码。这时必然存在传递函数依赖，否则码不是码，与3NF矛盾。故如果R是3NF关系模式，则R一定是2NF关系模式。

5、若Y(X1,X2,X3,X4)，(X1,X2)→X3，X2→X4；

（1）Y的候选码？
（2）属于第几范式？

解答

因为X2→X4，所以(X1,X2)→X4；
又因为(X1,X2)→X3，所以(X1,X2)→(X1,X2,X3,X4)。
因此：候选码：（X1,X2）；非主属性：X3,X4。
因为(X1,X2)→X4, X2→X4，存在非主属性X4对候选码（X1,X2）的部分函数依赖；
所以不属于2NF。
结论：候选码（X1,X2），属于第一范式。

6、R（A，B，C，D),F={AB→D，AC→BD，B→C}

（1） 侯选码？
（2）最高属于第几范式？

解答

因为B→C，AB→D，所以AB→CD。
故AB→ABCD
因为AC→BD，
故AC→ABCD。
因此候选码为AC和AB。
非主属性为D，不存在对候选码的部分函数依赖，最高为2NF。

7、R（X，Y，Z，W），F={Y←→W，XY→Z}

（1）侯选码？
（2） 最高属于第几范式？

解答

因为Y→W，XY→Z，
故XY→XYZW。
因为W→Y，XY→Z
故XW→XYZW；
因此候选码为XY和XW。存在传递函数依赖，最高为2NF。

8、R（A,B,C,D,E） F={A→B,CE→A,E→D}

（1） 求候选码。
（2）最高属于第几范式，为什么？
（3）分解到3NF。

解答

因为CE→A，A→B，E→D
故CE→ABCDE,
因此候选码为CE。
因为E→D，故存在非主属性对候选码的部分函数依赖，不是2NF，最高为1NF。
分解：
R₁(A,B)
R₂(C,E,A)
R₃(E,D)

9、R(商店编号，商品编号，数量，部门编号，负责人)

每个商店的每种商品只在一个部门销售，
每个商店的每个部门只有一个负责人，
每个商店的每种商品只有一个库存数量。
（1） 求候选码。
（2）R已达第几范式？为什么？
（3）若不属于3NF，分解成3NF。

解答

有R(Sno,Gno,Num,Dno,Name)
根据语义：(Sno,Gno)→Dno,(Sno,Dno)→Name,(Sno,Gno)→Num;
根据上面的条件，很明显候选码是(Sno,Gno)。其中存在传递函数依赖：由(Sno,Gno)得到Name的过程中。但不存在部分函数依赖，故是2NF。
分解：
R₁(Sno,Gno,Num,Dno);
R₂(Sno,Dno,Name).

10、R(A,B,C,D,E,F) F={A→C,AB→D,C→E,D→BF}

（1）写出候选码。
（2）分解到2NF。
（3）分解到3NF。
（4）分解到4NF。

解答

因为AB→D,A→C,
所以AB→ABCD.
又C→E,D→BF,
所以AB→ABCDEF.
又因为D→BF,A→C，
所以AD→ABCDF.
又C→E，
故AD→ABCDEF
所以候选码是AB与AD。
分解至2NF（去除部分函数依赖）：
R₁(A,B,D,F); R₂(A,C,E).
分解至3NF（去除传递函数依赖）：
R₁(A,B,D), R₂(D,F); R₃(A,C); R₄(C,E).
分解至4NF（去除多值依赖）：
R₁(A,B,D), R₂(D,F); R₃(A,C); R₄(C,E).
（刚刚符合3NF的模式也符合4NF）
 
 
参考文献：
[1]萨师煊，王珊，数据库系统概论.5版.北京:高等教育出版社,2014.
[2]David老师的PPT.